

剖析晶体振荡电路的设计
电子说
描述
本文主要参考资料:
- High-Performance Crystal Oscillator Circuits: Theory and Application, Eric A. Vittoz.
- Analog Design Essentials , Sansen
- ST应用笔记:ST微控制器振荡器电路设计指南
一. 晶振原理概述
在数字的世界里,无处不需要时钟,各种振荡电路的设计可以实现片内的集成,但是要实现高精度的时钟频率,晶体振荡器是很好的选择,时钟频率精度可以达到ppm级别。
石英晶体是一种将电能和机械能相互转化的压电器件,能量的转变发生在共振频率点上。石英晶体可以等效为电阻电容电感的串并联模型。
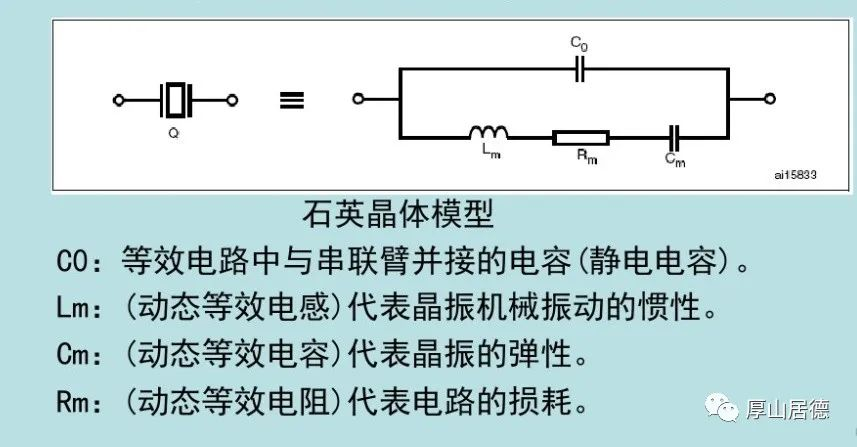
对于如上图所示的模型,可以得到晶振的阻抗和频率的关系图。
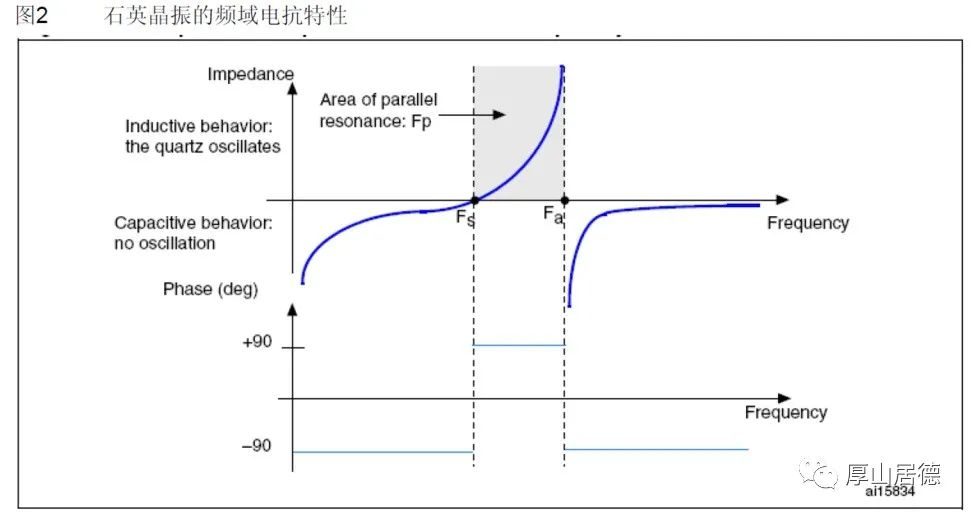
晶振的串联谐振频率为Fs, 并联谐振频率为Fa,在小于Fs和大于Fa的频率,表现为电容性,而在Fs和Fa之间,表现为电感性。对于晶振电路,希望工作在Fs和Fa之间,而靠近Fs的地方。在Fs到Fa之间的区域,称为晶振的“并联谐振区”,在这一区域晶振工作在并联谐振状态。晶振呈现电感特性,带来了180度的相移。频率的表达式为:
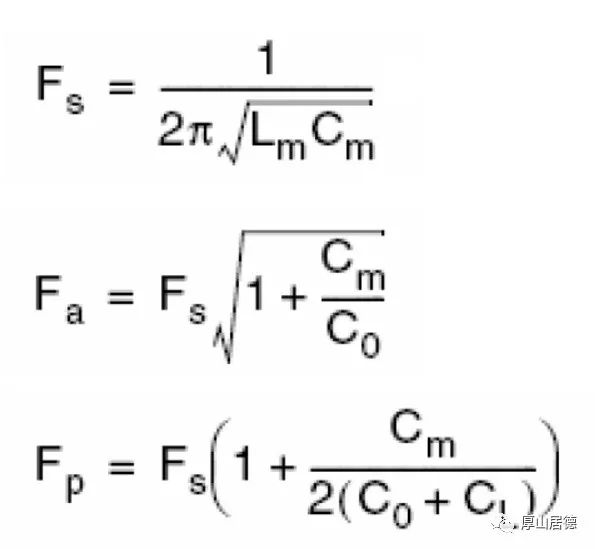
Fp就是我们晶振工作的频率,由于Fp中,其他参数确定,唯有Cl值可以调节,所以可以通过调整晶振的负载电容值Cl达到调节频率的目的。并且一般的温度补偿晶振电路也是通过调节Cl的值达到目的。
对于一个32.768K的晶振,按照模型参数仿真,对晶体模型两端加交流信号,可以仿真得到其阻抗随频率的曲线。和理论值一致。
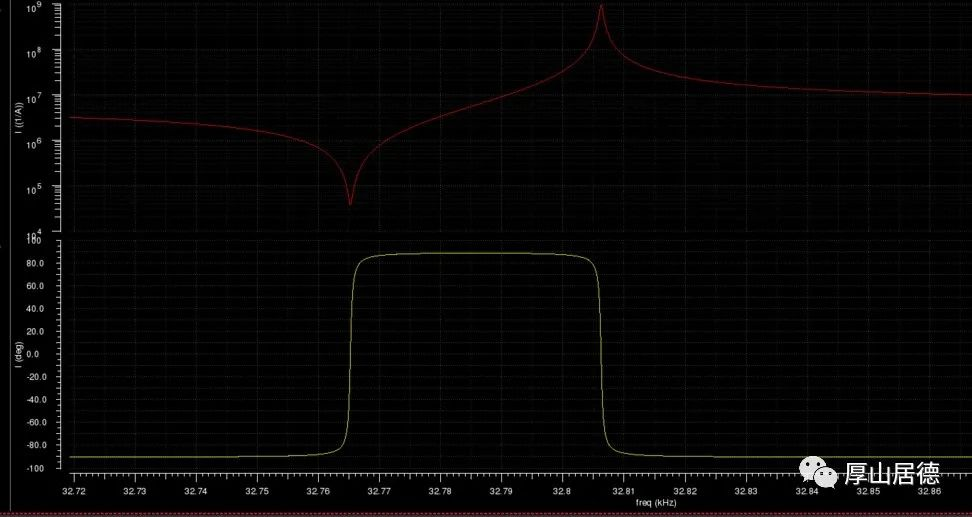
二. 晶体振荡电路的设计
在晶体振荡电路中,最常见的结构为Pierce振荡器。而对晶体振荡电路的分析,第一是使用负阻的概念,第二是使用增益与相位原理。
今天只说负阻法。
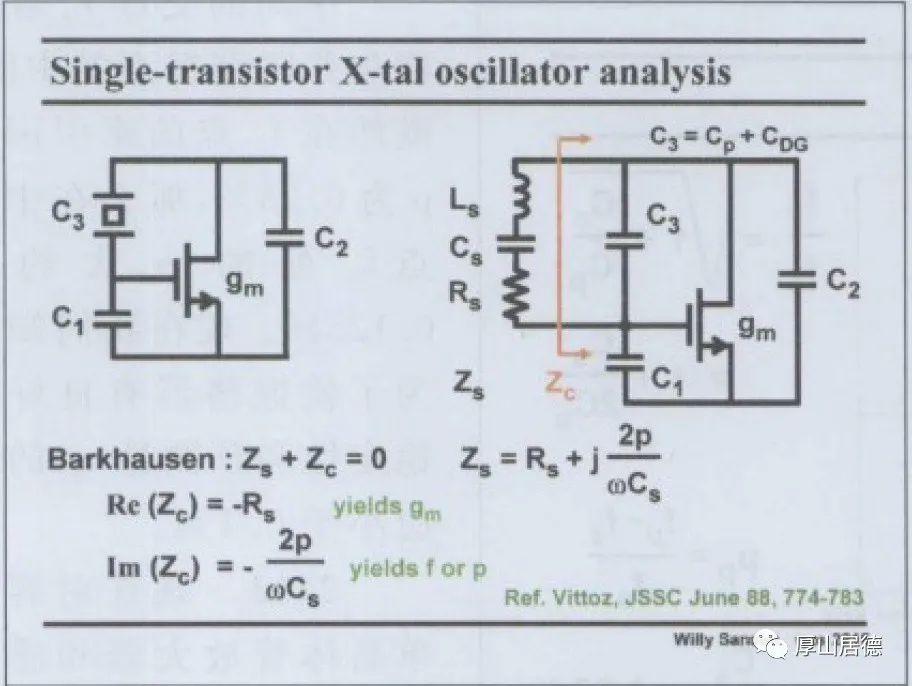
由于前面的分析,得到晶振在串联谐振频率处阻抗为Rs,则需要振荡电路提供-Rs的阻抗。而晶振发生了180的相移,在振荡频率出表现为电感的特性,则需要振荡电路提供电容的特性。
对于Pierce振荡电路的负阻的计算,如下图,在Razavi的书中有描述。
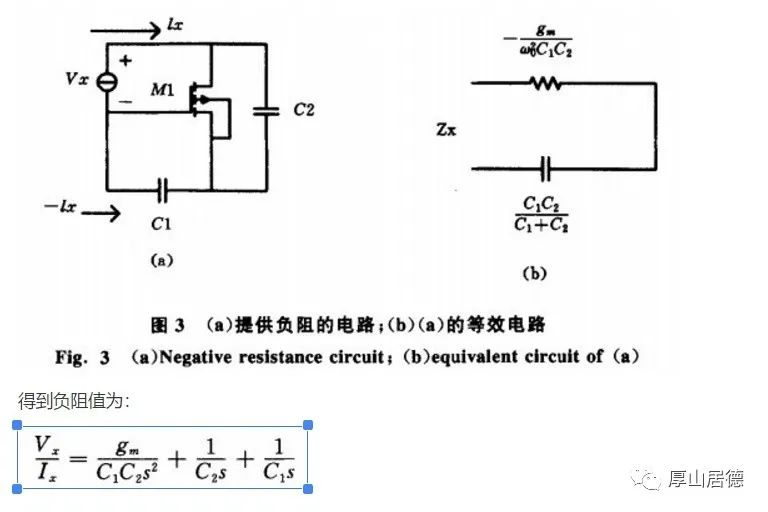
而在实际的应用中,还包括由晶振的C0以及MOS的Cgd和pcb上的杂散电容等形成的电容C3, 包含C3的电路的阻抗如下图所示。
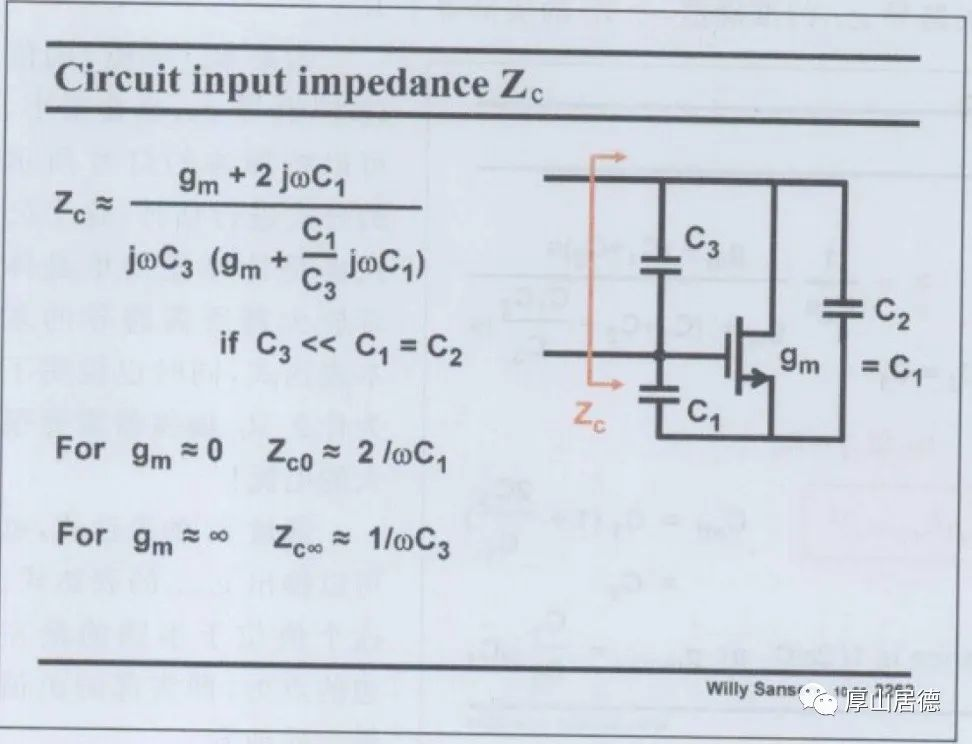
Zc值是一个关于gm的函数,取Zc的实部,得到的即是振荡电路的负阻值。关于Zc在复平面上,得到下面的图。
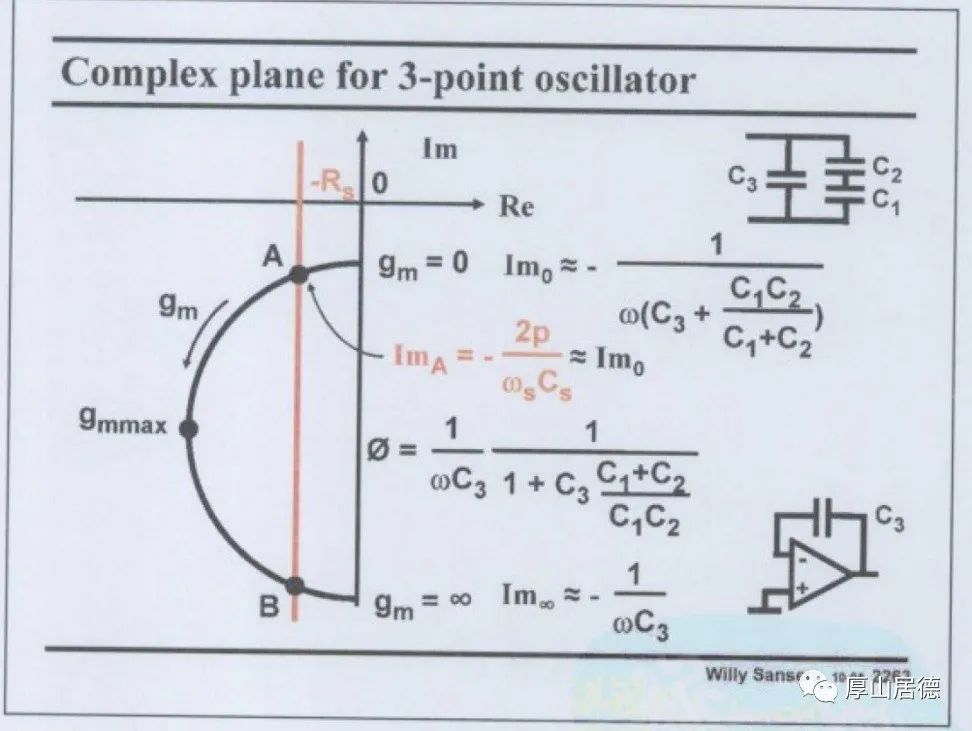
到这里,维持电路起振所需要的gm值可以近似计算出来,也可以通过matlab对上面的式子求解,得到精确的值。近似计算和matlab得到的值相差不大。
在Sanser的书中,近似计算表达式如下图,包括gma, gmmax,以及最大负阻值。(此公式可以容易地近似计算。)
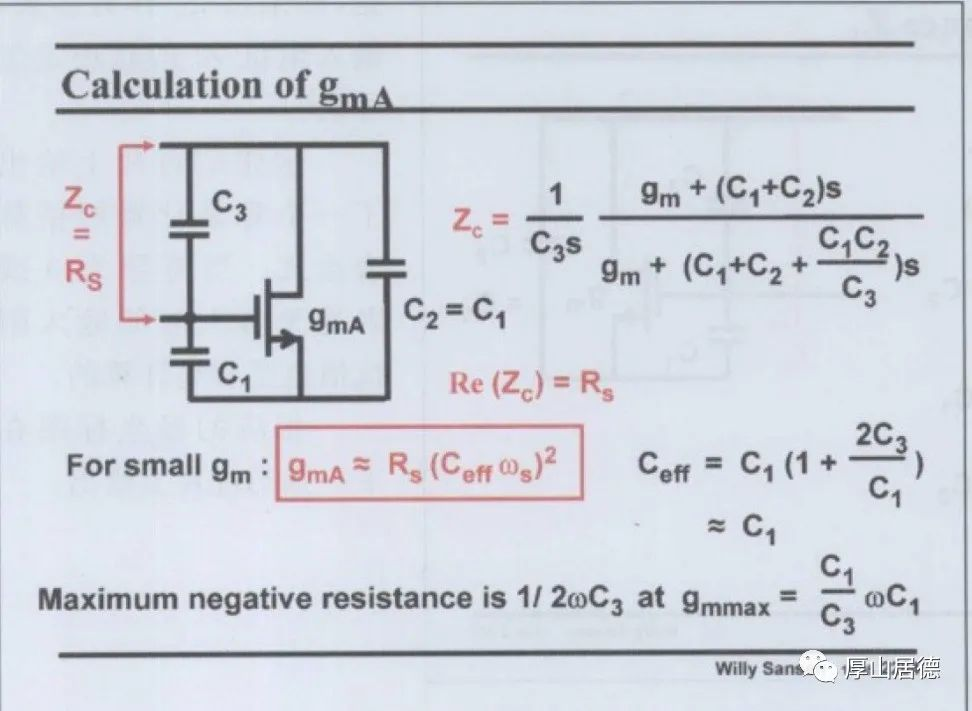
而在vittoz的论文中,给出的计算公式,可以精确计算出所需值。

设计示例:
下面给一个设计example。一个32.768K的晶振,datasheet上给出的参数为
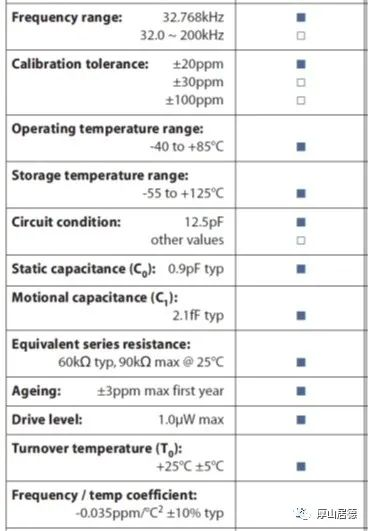
从表中得到:C1=C2=2*Cload=25pF, C0=0.9pF, Cs=2.1fF, Rs=60K.
使用matlab计算得到的值为
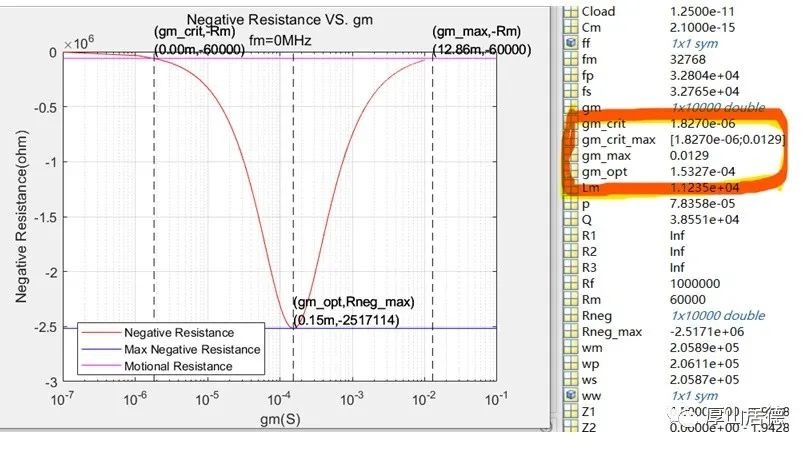
使用sansen书中的公式计算得到的值为:
gm_crit=1.6u, gm_max=12.9m, gm_opt=143u,
和matlab的计算值基本很接近,可以作为近似计算。
使用Vittoz论文中的公式计算得到的值为:
gm_crit=1.8266u, gm_max=12.9m, gm_opt=153.27u,
和matlab的计算值一致。
确定了电路的gm_crit值,也就是电路能起振的最小值后,在电路设计中,取实际的gm值约510倍gm_crit.即取gm约10u20u。
实际电路设计及仿真:
假设电路使用电流源驱动NMOS管。对于这类电路设计,一般提供gm的nmos管处于亚阈值区,所以gm值主要与电流值成正比。如果gm值按照计算出来的gm_opt取值,则需要的电流值大约,而在低功耗设计中,一般取5倍以上的最小gm值即可。本设计示例按照10倍取值,即gm=16uA/V。 仿真输入输出的gm=16uA/V, 稳态电流为1uA。同时仿真其负阻值为-510K, 大约也是10倍的晶振ESR电阻。
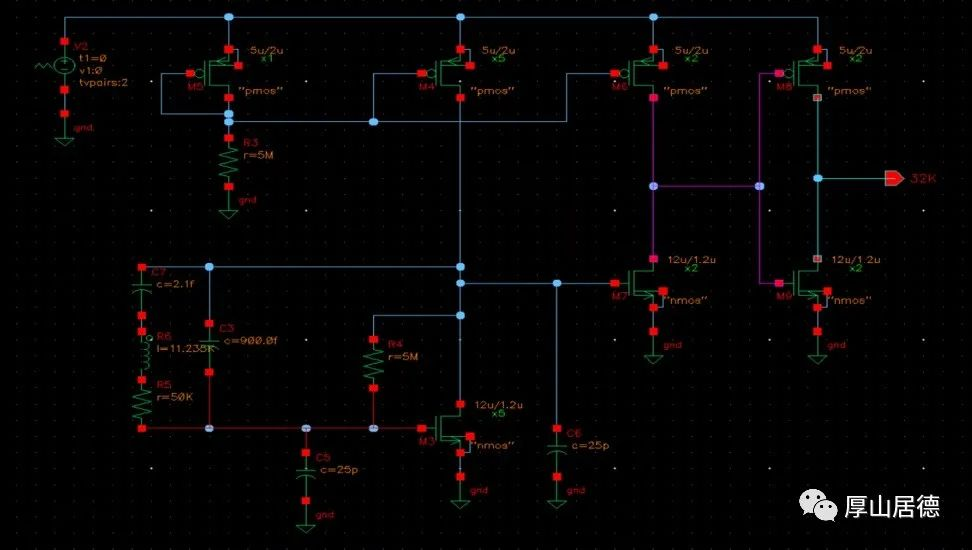
gm的仿真:输入加AC电压,加交流开关断开直流,输出利用交流开关接到地,测试输出的交流电流值。
负阻的仿真:输入输出加交流电流,测量输入输出的交流电压差,并使用计算器取实部(real函数),即可。也可以使用sp仿真,得到Z11的值。
最后对晶振电路进行瞬态仿真,可以观察晶振的起振过程。注意瞬态仿真时需要设置step=10ns。
晶振的DL:
还有一个重要的参数就是晶振的驱动级别DL,如果设计的电路,使得晶振的DL大于晶振要求的DL值,则晶振可能会损坏。

在晶振电路的设计中,最常见的一种电路结构如下图,可以看成一个反相器加反馈电阻做放大器,而外部的Rext的作用就是限制DL值。Rext的值可以用公式计算。
加入Rext后需要重新验证电路的gm值和负阻值是否满足起振要求。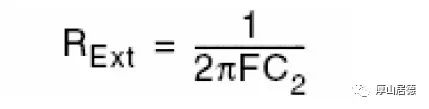
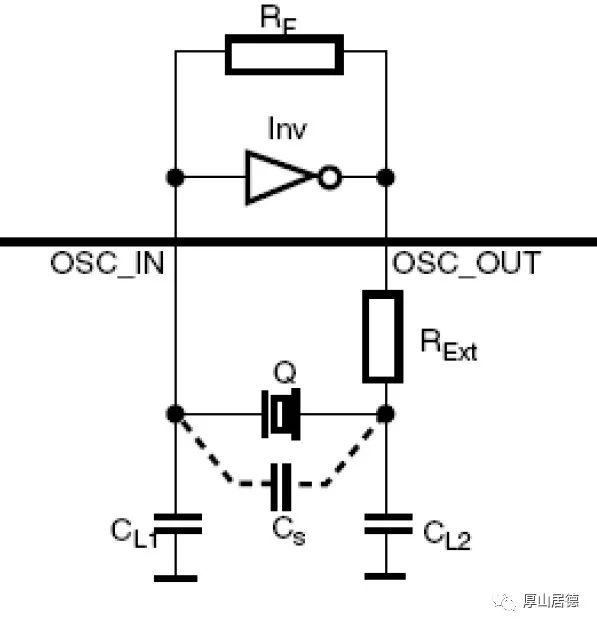
设计要点总结:
1.按照晶振的规格计算电路的gm值。
- 按照要求设计电路。
- 考虑DL,是否需要加入Rext电阻。
- 重新验证,整体仿真。
-
PCB上晶体振荡电路的设计2023-03-24 3339
-
晶体振荡电路设计指南2019-03-14 4737
-
晶体振荡电路设计_CN2015-12-25 1054
-
晶体振荡电路 求助!!2015-03-16 3269
-
有人懂晶体振荡电路吗?2011-12-13 4583
-
晶体振荡电路的设计方法2010-04-28 10987
-
晶体振荡电路的设计2009-06-28 12252
-
27MHz晶体振荡电路图2009-05-07 2685
-
泛音石英晶体振荡电路2008-08-17 3314
-
555晶体振荡电路2008-05-19 2145
全部0条评论

快来发表一下你的评论吧 !

