基于xWR1443毫米波雷达的参数估计与微多普勒仿真（MATLAB）

本文首发于公众号【调皮连续波】，其他平台为自动同步，内容若不全或乱码，请前往公众号阅读。保持关注调皮哥，和1.5W雷达er一起学习雷达技术！

 

2023年度会员内容更新公告（05.04）

序号	类别	内容	文件路径
1	雷达代码	本文内容	根目录雷达代码库

【正文】

编辑|雷达小助理  审核|调皮哥

---

 

代码运行平台：MATLAB2022a

操作系统：Windows 10 专业版

文件目录：

 

 

1、参数设置

 

雷达的参数按照原始数据采集的参数来设置，本文的MATLAB仿真中设置的雷达参数如下所示，同时设定了距离维和速度维的坐标轴。

•  
•  
•  
•  
•  
•  
•  
•  
•  
•  
•  
•  
•  
•  
•  
•  
•  
•  
•  
•  
•  

%% 参数设置n_chirps=128;                   %每帧脉冲数n_samples=256;                  %采样点数/脉冲N=256;                          %距离向FFT点数M=128;                          %多普勒向FFT点数
fs=10e6;                        %采样率c=3.0e8;                        %采样率f0=77e9;                        %初始频率lambda=c/f0;                    %雷达信号波长d=lambda/2;                     %天线阵列间距
Tc=50e-6;                       %单chirp周期Tf=40e-3;                       %帧周期B=1344.19e6;                    %信号带宽HzrangeRes=c/2/B*Tc/2*fs/N;       %距离刻度Ts=0127*Tc;                 %快时间轴Ta=0255*Tf;                 %总时间轴
Rr=0(N-1)*rangeRes;   %距离轴Vr=(-M/2:M/2-1)*lambda/Tc/M/2;  %速度轴

 

2、数据读取

 

数据读取采用TI官方提供的函数实现，在本文的仿真程序中采用readDCA1443()函数，得到4个接收通道的数据。

 

•  
•  
•  
•  
•  
•  
•  
•  
•  
•  
•  
•  

%% 数据读取fname='adc_data.bin'; %文件路径名称adcdata =readDCA1443(fname);n_frame=floor(length(adcdata)/n_chirps/n_samples); %数据总帧数
data_rx1= reshape(adcdata(1,:),n_samples,n_chirps,n_frame); %RX1数据data_rx2= reshape(adcdata(2,:),n_samples,n_chirps,n_frame); %RX2数据data_rx3= reshape(adcdata(3,:),n_samples,n_chirps,n_frame); %RX3数据data_rx4= reshape(adcdata(4,:),n_samples,n_chirps,n_frame); %RX4数据
%微多普勒数据profile=zeros(n_frame,n_chirps);

 

 

3、距离速度谱

 

利用距离维FFT和速度维FFT实现，其中在距离维FFT之前采用相量均值相消去除了零频，窗函数选择海明窗。仿真结果如下所示：

 

 

 

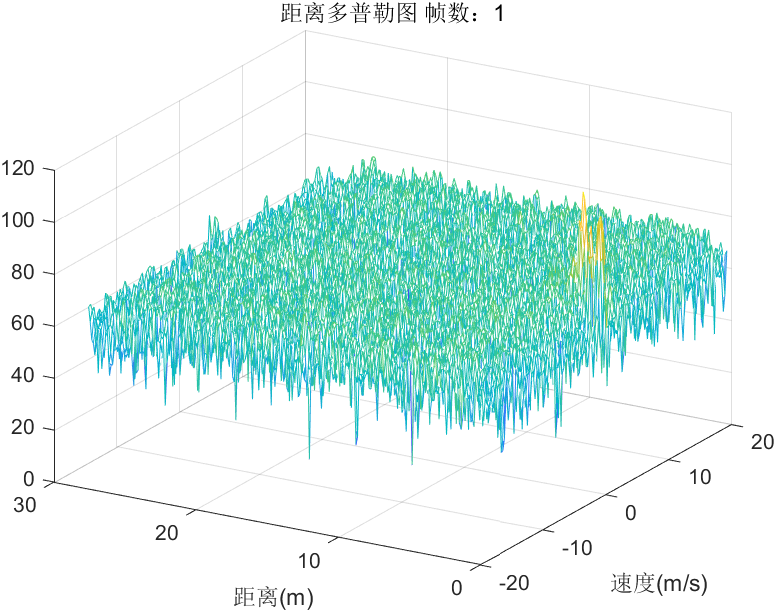
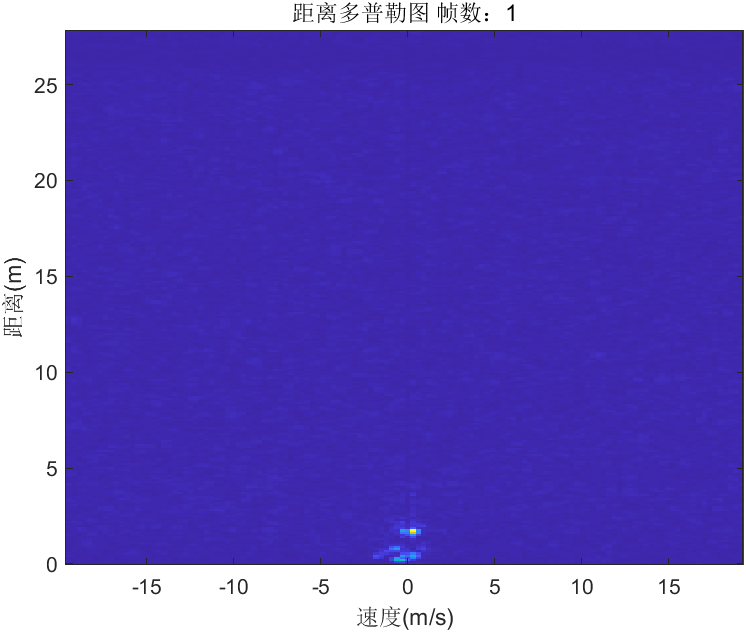
4、非相参积累

 

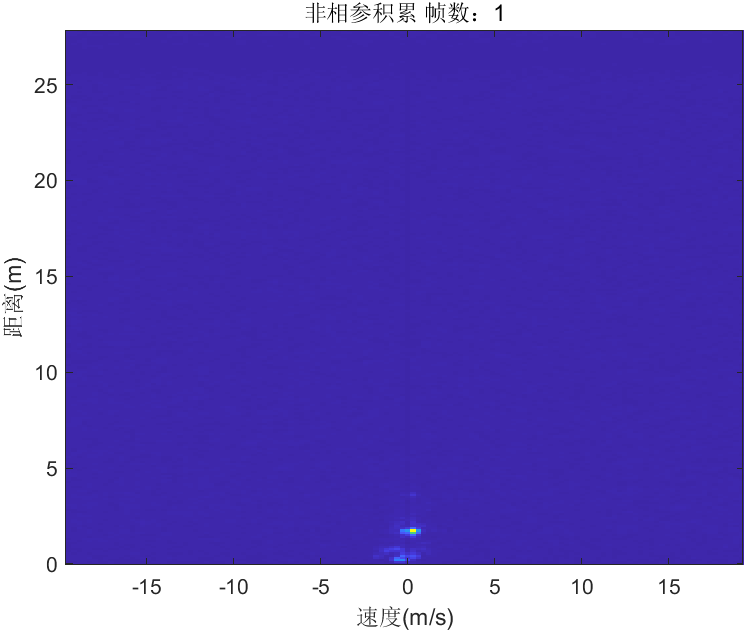
叠加四个通道的信号幅值，如下所示：

•  

 rx_2dfft=abs(rx1_2dfft)+abs(rx2_2dfft)+abs(rx3_2dfft)+abs(rx4_2dfft);

 

结果如下所示：

 

 

 

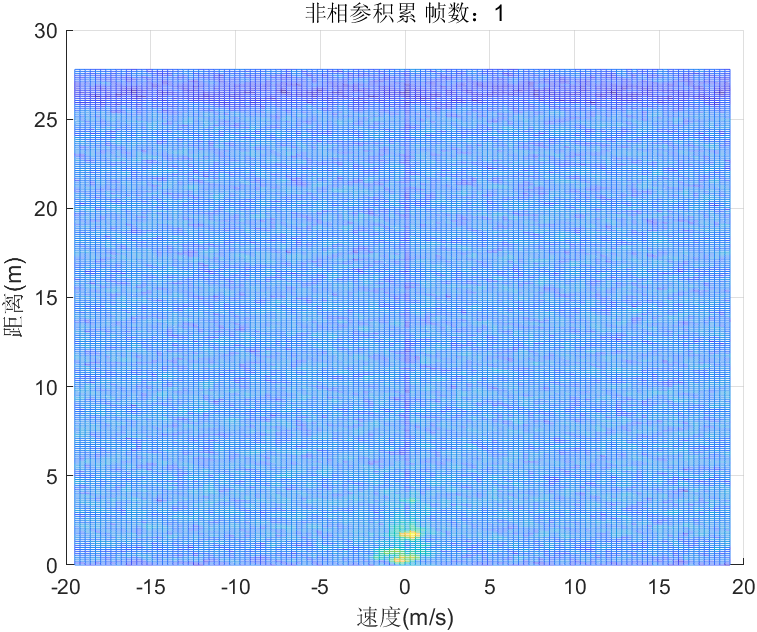
5、二维CFAR

 

CFAR参数根据雷达的分辨率等参数设定，本文仿真的参数设置如下所示，其中，虚警概率pfa =10^-6。

 

•  
•  
•  
•  
•  
•  
•  

%通过完整的距离多普勒图滑动窗口%在两个维度中选择参考单元的数量Tr = 8; Td = 4;%选择被测单元（CUT）周围两个维度的保护单元数量，以进行准确CFAR检测Gr = 4;Gd = 2;

 

结果如下所示：

 

 

2D CFAR的算法执行效率较低，读者可以根据需求选择先进行速度维CFAR，然后再进行距离维CFAR。

 

6、峰值搜索

 

首先建立检测矩阵，扩展补零，便于检测边界目标。

•  
•  

rx_2dcfar_temp=padarray(rx_2dcfar,[1,1],0);   %建立检测矩阵，扩展补零，检测边界目标[r,c]=size(rx_2dcfar);                        %矩阵大小

 

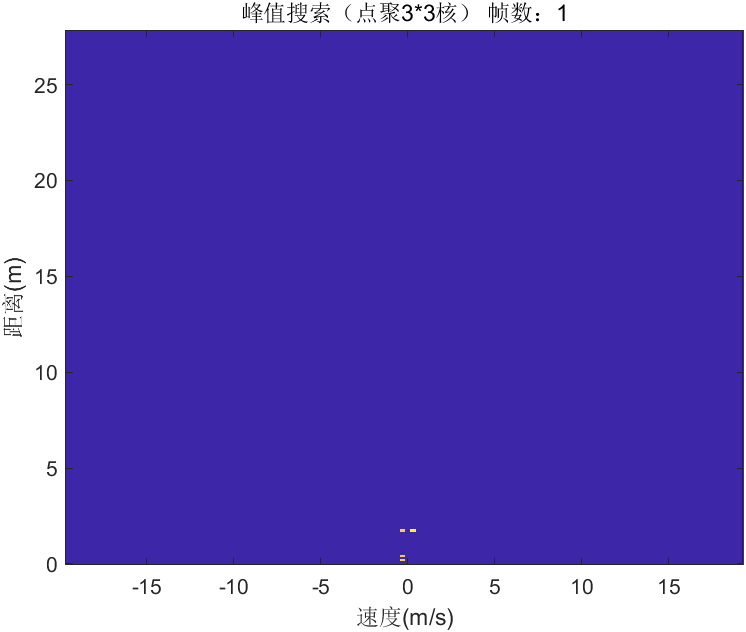
建立3*3的滑窗，通过找出滑窗内最大的值及其坐标，用于后续提取峰值点。

•  
•  
•  
•  
•  
•  
•  
•  
•  
•  
•  
•  
•  
•  
•  

for i=1:r                                     %创建3*3滑窗，找出较滑窗内数据最大值，剩余用0覆盖    for j=1:c        if  rx_2dcfar_temp(i+1,j+1)>0                               a=rx_2dcfar_temp(i:i+2,j:j+2);    %创建3*3滑窗            b=max(max(a));                    %找出较滑窗内数据最大值            [x,y]=find(a==max(max(a)));       %找出较滑窗内数据最大值在滑窗内坐标            temp=zeros(3,3);                  %创建3*3全0矩阵            rx_2dcfar_temp(i:i+2,j:j+2)=temp; %用3*3全0矩阵覆盖检测矩阵内数据，代表检测矩阵数据检测完成            temp(x,y)=b;                      %创建3*3全0保留最大值的矩阵            rx_2dcfar_temp(i:i+2,j:j+2)=temp; %用上述矩阵覆盖数据矩阵内数据，        end    endend
rx_2dcfar_plots=rx_2dcfar_temp(2:r+1,2:c+1);

 

效果如下所示：

7、微多普勒

 

微多普勒提取没有采用STFT法，而是直接提取RD谱中的低速部分速度，作为微多普勒。这种方法比较简单，也能在一定程度上近似微多普勒，工程上比较实用。

 

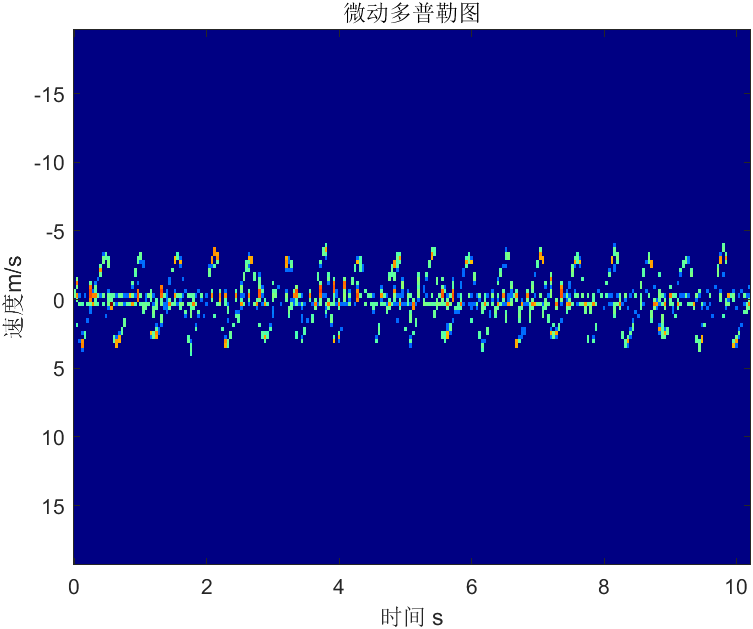
但是这种方法需要精细确定目标检测点的距离门分布范围，否则会漏掉一些目标点。例如，下面的代码中，j代表距离门范围。直接将每一帧的目标速度叠加起来，最后就能够得到近似的微多普勒谱。

 

•  
•  
•  
•  
•  
•  

  %微动多普勒forj=3:6    
   profile(n,:)=profile(n,:)+ rx_2dcfar(j,:);
end

 

仿真结果如下图所示：

 

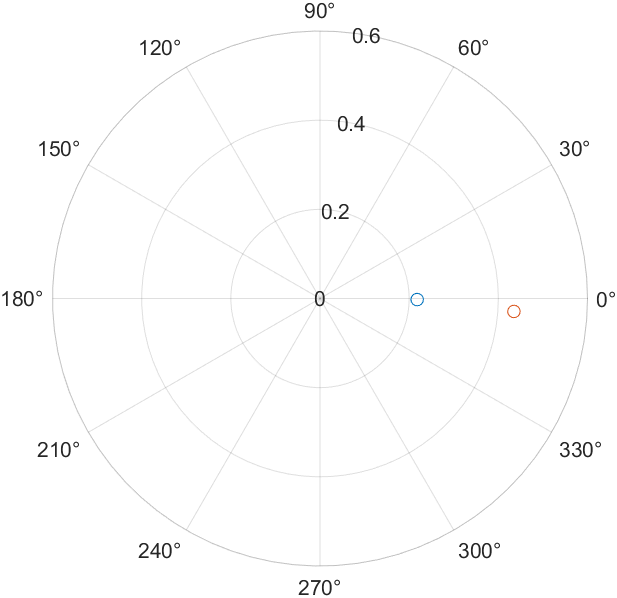
8、角度估计

 

采用角度维FFT，角度估计的其他方法，比如DBF、Capon、MUSIC、压缩感知以及其他超分辨算法等，需要读者自行探索，公众号以往的一些文章也提到过一些，可以参考。

 

 

9、微多普勒速度时域包络

 

利用微多普勒频率fd乘以速度v ，可以得到fd*v = 2(v^2)/λ，即得到了以2/λ为幅度系数的微多普勒速度包络v^2,也就是微多普勒速度的功率，如下图所示。

 

 

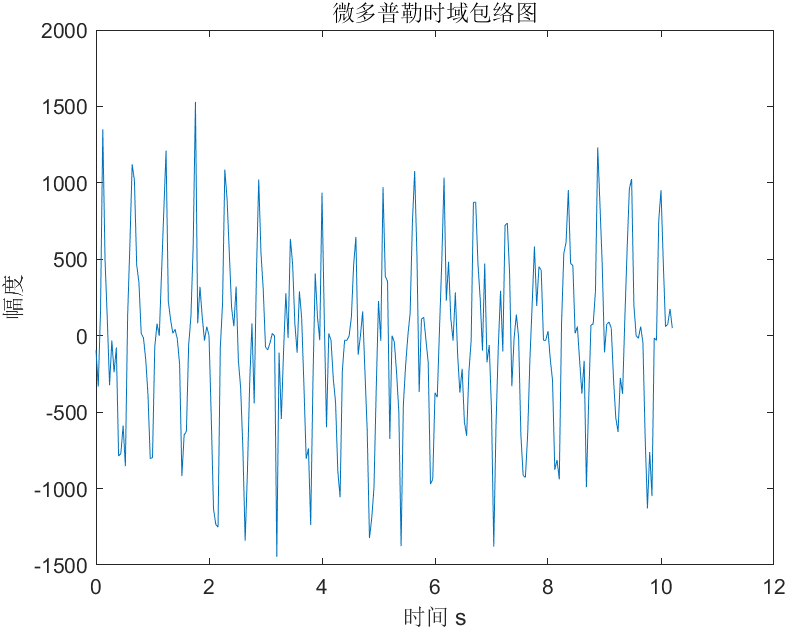
包络检波得到的是带通信号的基带部分，在本文中也就是微多普勒速度的时域信号。

 

10、微多普勒调制频谱图

 

微多普勒速度频域可以利用对微多普勒速度时域信号做FFT求得，而实信号FFT得到双边谱，如下图所示。

 

•  
•  
•  
•  
•  
•  
•  
•  
•  
•  
•  
•  
•  
•  
•  
•  
•  
•  

% 微动多普勒绘图profile=profile';figure(8)colormap(jet);imagesc(Ta,Vr,(profile));title('微动多普勒图');xlabel('时间 s');ylabel('速度m/s');
profile_x=Vr*profile;%微动多普勒与速度乘积累加figure(9)plot(Ta,profile_x);xlabel('时间 s');ylabel('幅度');title("微多普勒时域包络图")
profile_x=fftshift(fft(fftshift(profile_x,256)));  %FFTFs=1/(Tf*256);F=(-128:127)*Fs; %频率轴figure(10)plot(F,(abs(profile_x)));title("微多普勒频域图");xlabel("频率 Hz");ylabel("幅值");

 

 

 

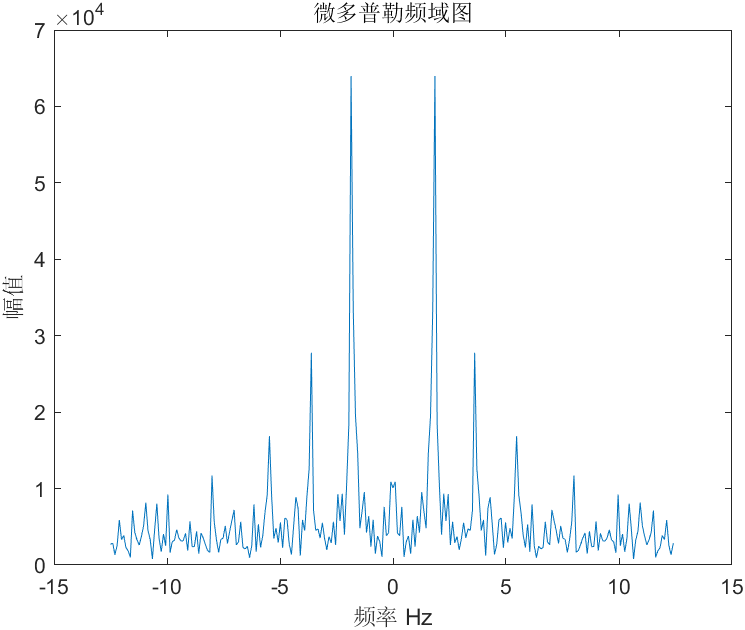
这个谱图的峰值表示，微多普勒频率，可以看到上图，峰值较强的有4个。

 

本文到此结束，年度会员直接查看公告目录，非会员可私信博主。

 

【点击以下链接可直达各个业务模块】

 

加入雷达群	加入年度会员
雷达项目交流	付费咨询
商业推广合作	文章投稿指南

【本期结束】

---

本文是空闲时个人的心得体会，仅供参考。目前我还有很多内容需要学习，如果还有没有说到或者不全面的地方，还请指正，感谢大家。

 

喜欢本文，可以转发朋友圈。欢迎关注【调皮连续波】和备用号【跳频连续波】。

---

审核编辑 黄宇