支持向量机寻找的最优分类直线应满足哪些条件？

支持向量机寻找的最优分类直线应满足如下条件：

（1）该直线可将训练数据完全分为两类。

（2）该直线可最大化间隔。

（3）该直线处于间隔的中间，其与所有支持向量（任意一条可将训练样本完全分类的直线分别向两侧被平行移动时，最先穿过的一个或几个训练样本）的距离相等。

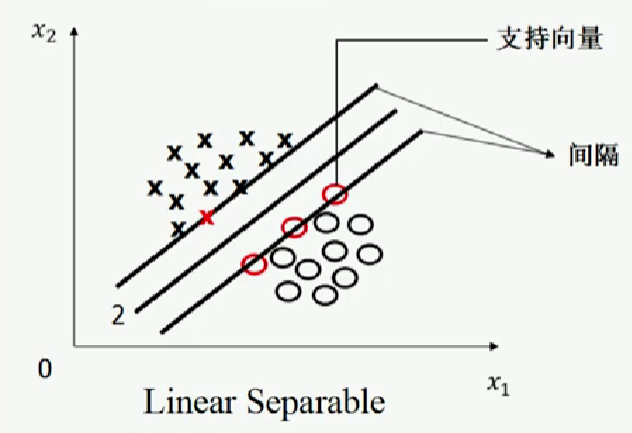
图片来源：中国慕课大学《机器学习概论》

可推出支持向量机寻找最优分类超平面（超平面是将三维以上特征空间的训练数据分割为不同类别的“图形”）应满足如下条件：

（1）该超平面可将训练数据完全分为两类。

（2）该超平面可最大化间隔。

（3）该超平面处于间隔的中间，其与所有支持向量的距离相等。

下文介绍通过数学方法，将支持向量机寻找线性可分训练数据集的最优分类超平面的过程，描述为最优化问题。

回顾线性可分的定义：训练样本集 {(Xi,yi)}在i=1~N线性可分是指存在ω和b（Xi=[xi1，xi2,…,xin]，ω=[ω1，ω2,…,ωn]T），使得对 i=1~N，有：

若yi=+1，则ωTXi+b>0；

若yi=-1，则ωTXi+b<0。

同时，基于以下两个事实：

事实1：ωTx+b=0与(aωTx)+(ab)=0是同一个超平面（a≠0）。（此事实可基于二维特征空间的情况理解，当a≠0时，二维特征空间中，ωx+b=0与aωx+ab=0是同一条直线）

事实2：一个点X0到超平面ωTx+b=0的距离d的公式为：d=|ωTX0+b|/||ω||，其中||ω||2=ω12+ω22…+ωn2。（此事实也可基于二维特征空间的情况理解，二维特征空间中，一个点(x0,y0)到ω1x0+ω2y0+b=0的距离为：d=|ω1x0+ω2y0+b|/√(ω12+ω22)，√代表根号）

因为ωTx+b=0与(aωTx)+(ab)=0是同一个超平面，所以可以通过缩放（即直线方程两端均乘以相同系数），使得ωTx+b在支持向量x0上有|ωTx0+b|=1（根据线性可分的定义，支持向量x0上有|ωTx0+b|＞0，假设|ωTx0+b|=0.5，那么可以通过将该方程两端均乘以2缩放为|ωTx0+b|=1，其他情况均可以此类推）。

那么，根据事实2，支持向量x0到超平面的距离d=|ωTx0+b|/||ω||=1/||ω||。因此，最大化支持向量至超平面的距离（即最大化超平面的间隔）等价于最小化||ω||。

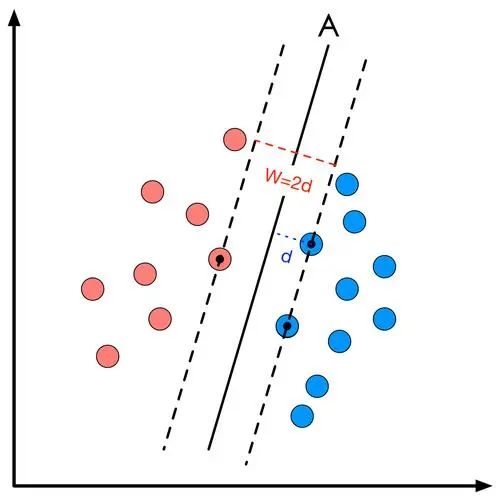
图片来源：来自网络

因此，支持向量机寻找线性可分训练数据集的最优分类超平面的过程可描述为最小化1/2||ω||2（最小化1/2||ω||2即可使||ω||最小化）的最优化问题。

又因为非支持向量与超平面的距离大于支持向量与超平面的距离，所以非支持向量与超平面的距离d>1/||ω||，即在非支持向量x0上有|ωTx0+b|>1。

综合支持向量与非支持向量距离取值，可得出支持向量机寻找线性可分训练数据集的最优分类超平面的限制条件：yi(ωTXi+b)≥1，i=1~N。

综上，在线性可分情况下，支持向量机寻找最佳超平面的优化问题可以表示为 :

最小化：1/2||ω||2，

限制条件：yi(ωTXi+b)≥1，i=1~N。

上述优化问题中，ω和b为待求量， (Xi,yi)，i=1~N为已知量。该优化问题属于凸优化问题（CONVEX OPTIMIZATION）。当一个问题转化为凸优化问题时，该问题可使用机器学习算法的工具包求解。

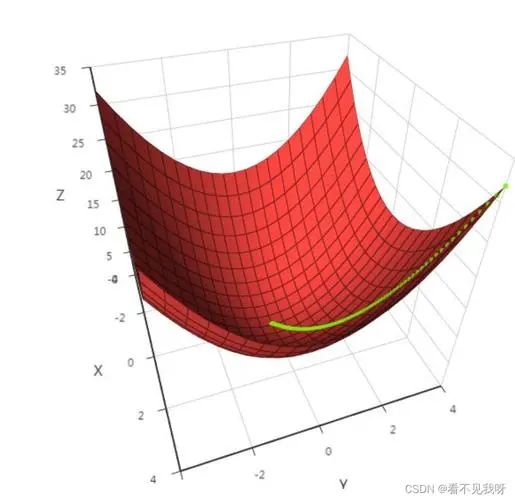
图片来源：来自网络

审核编辑：刘清