

激光雷达SLAM中高效的点云数据结构
描述
k-d树是一种常用的多维数据结构,它可以用于范围搜索、最近邻搜索等问题。但是,在实际应用中,我们经常需要对动态数据进行查询和修改操作。这时候,传统的k-d树就显得力不从心了。为了解决这个问题,研究人员提出了动态k-d树(Dynamic k-d Tree)这一概念。与传统的k-d树不同,动态k-d树可以支持插入、删除和修改操作,并且能够保持平衡状态。动态k-d树可以用于各种多维数据结构问题,例如范围搜索、最近邻搜索等。本文将介绍动态k-d树的基本原理、实现方法。
1 基本原理
1.1 k-d树
首先,我们来回顾一下传统的k-d树。k-d树是一种二叉搜索树,它将每个节点表示为一个超矩形,并按照某种规则将超矩形划分成两个子区域。具体来说,k-d树的构建过程如下:
选择一个维度d,将数据集按照第d个维度的值进行排序。
选择中位数作为根节点,并将数据集分成两个子集。左子集包含小于中位数的所有数据,右子集包含大于中位数的所有数据。
对左右子集递归执行步骤1和步骤2,直到每个节点只包含一个数据点
在k-d树中,每个节点都表示一个超矩形,其中包含了一些数据点。对于任意一个节点,它的左子树和右子树所代表的超矩形是不相交的。因此,在搜索时,我们可以通过比较查询点与当前节点所代表的超矩形的位置关系来确定搜索方向。例如,在二维平面上构建k-d树时,每个节点都代表一个矩形区域。如果查询点在当前节点所代表的矩形区域的左下角,则搜索方向为左子树;如果查询点在右上角,则搜索方向为右子树。
1.2 动态k-d树
传统的k-d树只能处理静态数据集,即数据集不会发生变化。但是,在实际应用中,我们经常需要对动态数据进行查询和修改操作。例如,在机器人运动规划中,机器人需要不断地获取周围环境信息,并进行路径规划。这时候,传统的k-d树就无法满足需求了。
为了解决这个问题,研究人员提出了动态k-d树(Dynamic k-d Tree)这一概念。与传统的k-d树不同,动态k-d树可以支持插入、删除和修改操作,并且能够保持平衡状态。
在动态k-d树中,每个节点都代表一个超矩形区域,其中包含了一些数据点。与传统的k-d树不同的是,动态k-d树中的节点可以被插入、删除或修改。当一个节点被插入时,我们需要重新构建整个树;当一个节点被删除时,我们需要将其从树中移除,并重新平衡整个树;当一个节点被修改时,我们需要更新其所代表的超矩形区域,并重新平衡整个树。
2. ikd-Tree设计与实现
ikd-Tree是一种基于K-D树的动态数据结构。它由一个二叉搜索树组成,在每个节点上存储一个超矩形区域和一个点集合。超矩形区域是由该节点所代表的所有点确定的最小超矩形区域。每个节点都有一个划分轴和划分值来将其子节点分成两个子集。ikd-Tree的基本结构,包括节点、分割平面和子树等和一些增量操作,包括插入、重新插入和删除等。在这些操作中,ikd-Tree使用递归算法来更新节点,并通过旋转和重建子树来保持平衡。此外,该节还介绍了如何进行动态重新平衡,以避免树的不平衡导致查询效率下降。最后,该节讨论了如何使用ikd-Tree进行最近点搜索。ikd-Tree 中树节点的属性在下表中给出。第 2-4 行是标准 k-d 树的公共属性。属性 left tson 和 rightson 分别是指向它的左子节点和右子节点的指针。点信息(例如点坐标、强度)存储在点中。由于一个点对应于 k-d 树上的单个节点,因此我们将互换使用点和节点。划分轴记录在axis中。第 5-7 行是为第 III-C 节中详述的增量更新而设计的新属性。

2.1 增量更新和重新平衡
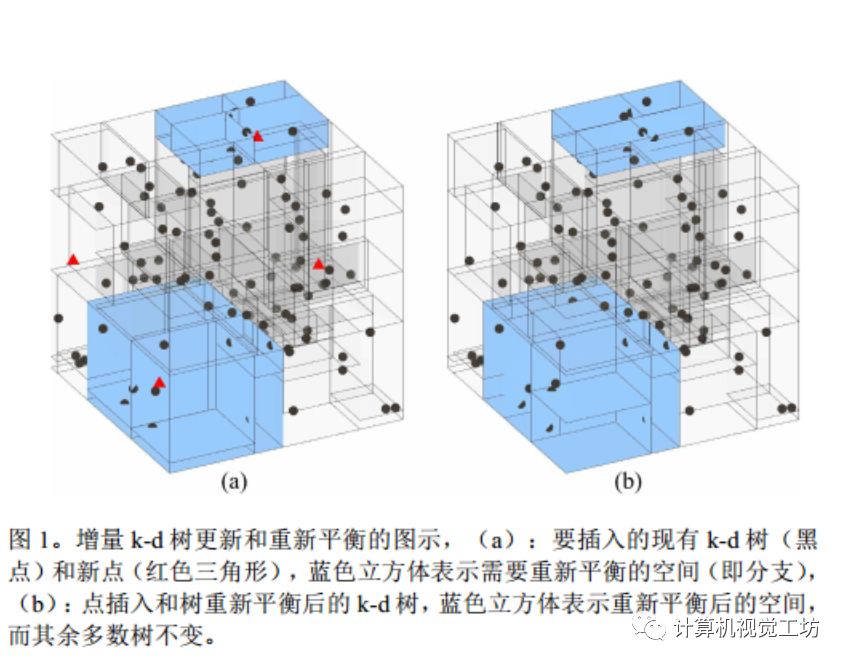
图1展示了增量k-d树的更新和重新平衡过程。在这个例子中,黑色点表示现有的k-d树节点,红色三角形表示要插入的新点。蓝色立方体表示需要重新平衡的空间(即分支)。在插入新点后,ikd-Tree使用旋转和重建子树来保持平衡,并将蓝色立方体移动到正确的位置。
2.2 盒式操作和下采样
盒式操作是指将空间划分为多个盒子,以便更快地搜索最近的点。在ikd-Tree中,这是一种针对数据坐标轴对齐的矩形框内的所有点进行插入、删除或重新插入操作的方法。这些矩形框可以由用户指定,也可以根据数据集自动计算得出。下采样是指在保持数据分布的同时减少数据量,从而提高查询效率。
2.3 动态重新平衡
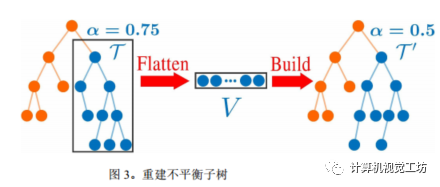
ikd-Tree还支持动态重新平衡,以避免树的不平衡导致查询效率下降。具体来说,ikd-Tree使用部分重建方法来重新平衡树。当需要重新平衡时,ikd-Tree将树分成两个部分,并在两个线程中同时进行重建操作。这种方法可以最大限度地减少重建时间,并提高整体效率。
3 时间和空间复杂度
该节介绍了ikd-Tree分别对插入、删除、查询和重建等操作的时间复杂度进行了分析。最后,该节还讨论了ikd-Tree的空间复杂度和实际应用中的性能表现。ikd-Tree是一种基于k-d树的增量数据结构,可以在机器人应用中高效地进行点云数据处理、路径规划等操作。
在ikd-Tree中,每个节点都包含一个分割平面和两个子树,其中左子树包含小于分割平面值的点,右子树包含大于等于分割平面值的点。通过递归算法,在每个节点上进行二分查找,并通过旋转和重建子树来保持平衡。在插入操作方面,该节指出,在最坏情况下,插入一个新点需要O(n)次比较操作(其中n表示树中节点数目)。这是因为新点可能会被插入到所有节点的左或右子树中。但是,在实际应用中,由于ikd-Tree使用动态重新平衡方法来保持平衡,并且支持下采样等功能来减少数据量,因此插入操作的时间复杂度通常为O(log n)。
在删除操作方面,该节指出,删除一个节点需要O(log n)次比较操作。这是因为ikd-Tree使用递归算法来查找要删除的节点,并通过旋转和重建子树来保持平衡。但是,在实际应用中,由于ikd-Tree支持下采样等功能来减少数据量,因此删除操作的时间复杂度通常为O(log n) 在查询操作方面,该节指出,ikd-Tree的查询操作需要O(log n)次比较操作。这是因为在每个节点上进行二分查找,并根据分割平面的值来选择左或右子树进行递归查找。由于ikd-Tree使用动态重新平衡方法来保持平衡,并且支持下采样等功能来减少数据量,因此查询操作的时间复杂度通常为O(log n)。
在重建操作方面,该节指出,ikd-Tree使用部分重建方法来重新平衡树。当需要重新平衡时,ikd-Tree将树分成两个部分,并在两个线程中同时进行重建操作。这种方法可以最大限度地减少重建时间,并提高整体效率。由于ikd-Tree支持动态重新平衡和部分重建等功能,因此重建操作的时间复杂度通常为O(log n)。
在空间复杂度方面,该节指出,ikd-Tree需要O(n)的空间来存储所有节点和数据点。每个节点都需要存储其分割平面、子树信息以及其他元数据。但是,在实际应用中,由于ikd-Tree支持下采样等功能来减少数据量,并且可以通过压缩存储等技术进一步减少所需存储空间。
欢迎关注「3D视觉工坊」,加群/文章投稿/课程主讲,请加微信:dddvisiona,添加时请备注:加群/投稿/主讲申请
实验结果与分析
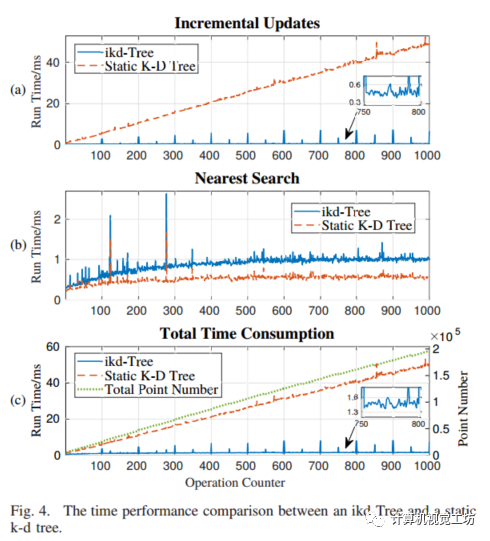
该节首先介绍了测试环境和数据集,包括使用的硬件和软件配置以及测试数据的来源和特点。然后,该节详细讨论了ikd-Tree在不同应用场景下的性能表现,并与其他数据结构进行了比较。这些实验分别是基于随机增量数据集的实验和基于LiDAR测距仪的室外SLAM实验。在随机增量数据集实验中,ikd-Tree的效率得到了充分验证。该实验使用1000个点作为初始数据集,并逐步增加1000个点进行测试。图4(a)展示了ikd-Tree和静态k-d树之间的运行时间比较,其中x轴表示增量更新次数,y轴表示运行时间(单位:毫秒)。
可以看出,在增量更新次数较少时,ikd-Tree和静态k-d树之间的运行时间差异不大。但是,当增量更新次数达到一定数量时,ikd-Tree明显优于静态k-d树,并且具有更好的扩展性。图4(b)展示了ikd-Tree和静态k-d树之间的最近邻搜索时间比较,其中x轴表示查询次数,y轴表示运行时间(单位:毫秒)。可以看出,在查询次数较少时,ikd-Tree和静态k-d树之间的查询时间差异不大。但是,在查询次数达到一定数量时,ikd-Tree明显优于静态k-d树,并且具有更好的扩展性。图4(c)展示了ikd-Tree和静态k-d树之间的操作计数和总时间消耗比较,其中x轴表示点数,y轴表示操作计数和总时间消耗。在点数达到一定数量时,ikd-Tree明显优于静态k-d树。
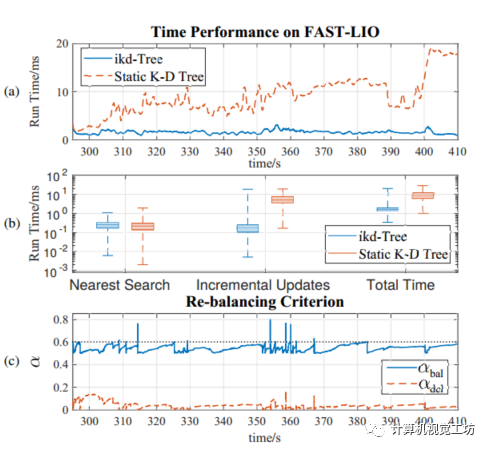
在LiDAR的室外SLAM实验中,ikd-Tree也表现出了优异的性能。该实验使用了一个移动机器人和一个LiDAR,通过对周围环境进行扫描来构建地图。图5展示了ikd-Tree在该实验中的性能表现,其中x轴表示时间(单位:秒),y轴表示运行时间(单位:毫秒)。可以看出,在整个实验过程中,ikd-Tree的运行时间始终保持在较低水平。
审核编辑:刘清
-
浅析自动驾驶发展趋势,激光雷达是未来?2017-09-06 5378
-
激光雷达是自动驾驶不可或缺的传感器2017-09-08 5180
-
常见激光雷达种类2017-09-25 13817
-
激光雷达面临的机遇与挑战2017-09-26 6582
-
激光雷达究竟为什么这么牛,这么贵2017-10-16 7002
-
消费级激光雷达的起航2017-12-07 7303
-
激光雷达除了可以激光测距外,还可以怎么应用?2018-05-11 5960
-
5 款激光雷达:iDAR、高清3D LiDARInnovizPro、S3、SLAM on Chip、VLS-1282018-07-26 5962
-
AGV激光雷达SLAM定位导航技术2018-11-09 9871
-
【北醒TFmini-S 测距/避障激光雷达传感器免费试用连载】基于FPGA平台的YOLO-Complex点云数据加速2020-05-28 2677
-
激光雷达知多少:从技术上讲讲未来前景2020-07-14 41508
-
当“思岚”激光雷达邂逅盲人拐杖2021-11-12 3965
-
激光雷达点云数据分割算法的嵌入式平台上的部署实现2021-12-21 2483
-
详解激光雷达点云数据的处理过程2023-03-14 5549
-
激光雷达点云数据包含哪些信息2024-08-29 2562
全部0条评论

快来发表一下你的评论吧 !

