一文详解RC微分电路

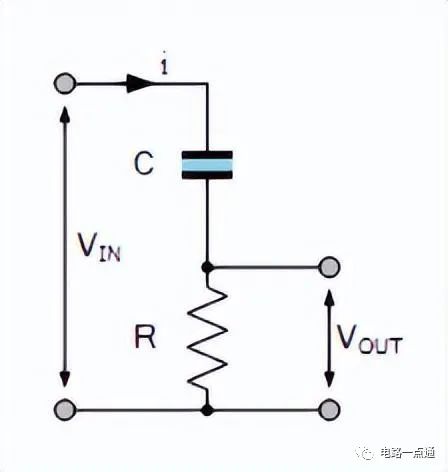
对于无源 RC 微分器电路，输入连接到电容器，而输出电压取自与 RC 积分器电路完全相反的电阻两端。

就像之前说的，你看完硬件工程师jack：RC积分电路之后，其实带着一个思考的角度去想，如果看看R上的分压会是什么样呢?

其实这个想法最终的实现就是“RC微分电路”，道理呢也非常简单，把RC这条之路看成一个二端口网络，那么其电压就是输入电压Vin。 既然C上的电压是积分形式的：

那R上的电压就是微分的形式。

RC 微分器电路

对于 RC 微分器电路，输入信号施加到电容器的一侧，输出跨接在电阻器上，然后 V OUT等于 V R。 由于电容器是频率相关元件，因此在极板上建立的电荷量等于电流的时域积分。 也就是说，电容器需要一定的时间才能充满电，因为电容器不能瞬间充电，只能按指数方式充电。

电阻电压

前面我们说过，对于RC微分器，输出等于电阻两端的电压，即：VOUT等于VR并且是一个电阻，输出电压可以瞬时变化。

然而，电容器两端的电压不能立即改变，而是取决于电容值 C，因为它试图在其极板上存储电荷 Q。 然后流入电容器的电流，即它取决于其极板上电荷的变化率。 因此，电容器电流与电压不成正比，而是与其时间变化成正比：i = dQ/dt。

由于电容器板上的电荷量等于Q = C x Vc，即电容乘以电压，我们可以推导出电容器电流的方程式

上式其实就是RC微分电路的公式。

而RC常数就是固定常量RC。

简单仿真单脉冲输入

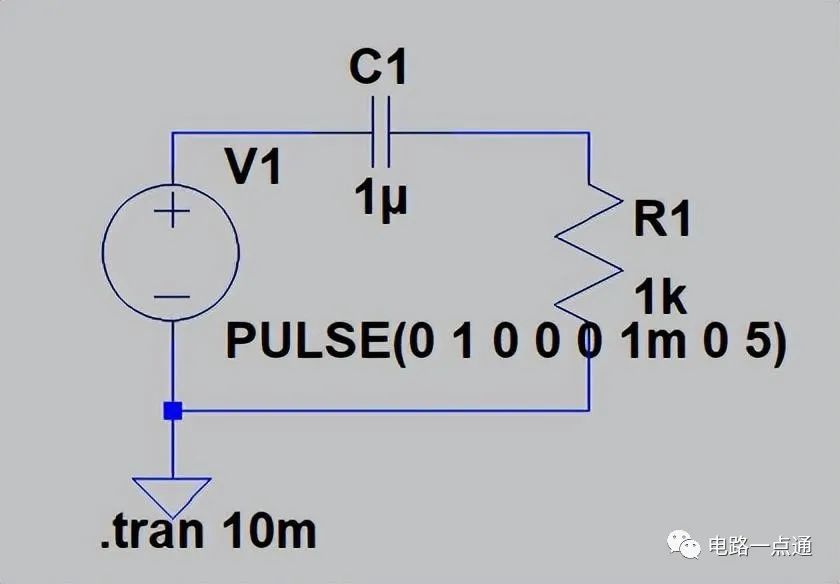
简单仿真一下，我们用一个脉宽为1ms的1V方波给该电路充电：充电波形

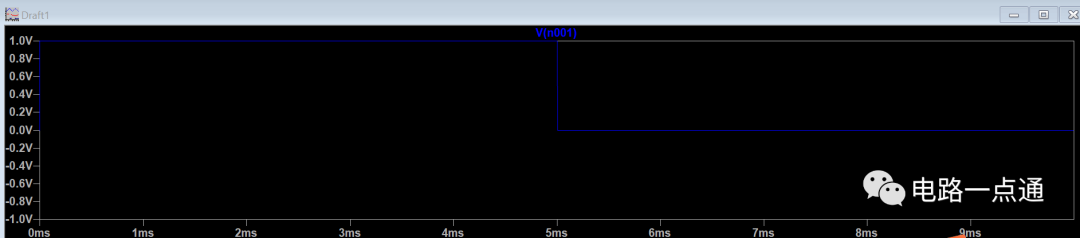
再看一下输出的电阻上的波形：

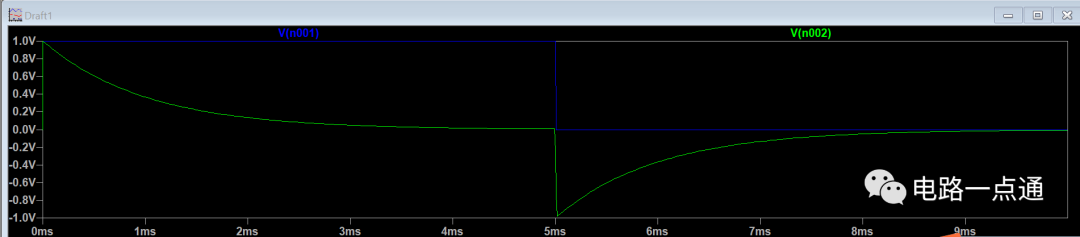
可以看到电阻上一开始是接近于输入电压的波形，后面慢慢减小。

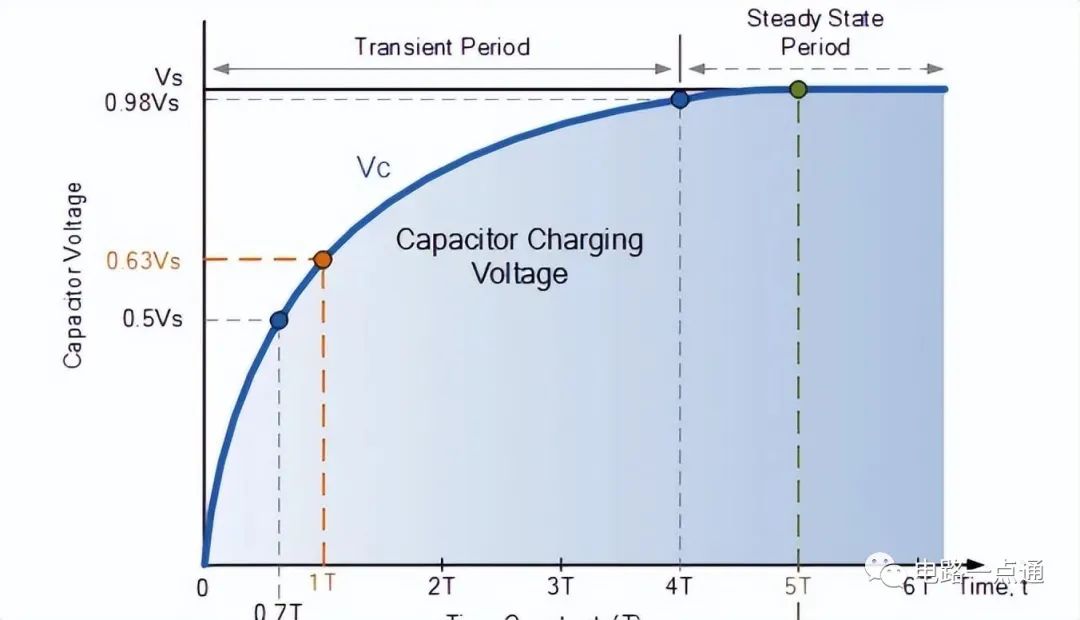
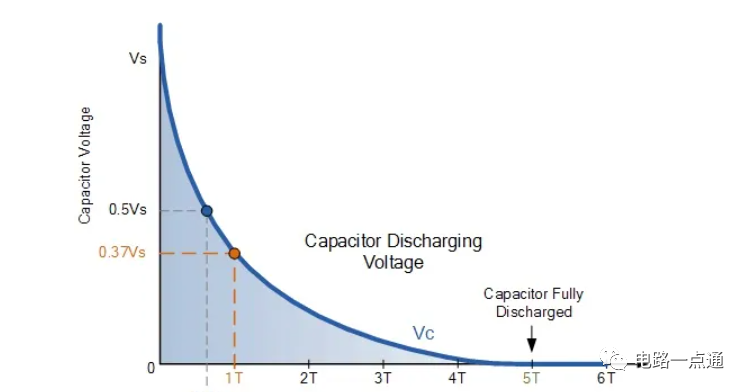
再根据RC放电电路的知识，我们知道，在一τ的时间，也就是一个RC，电压应该下降到0.37V如下图(τ=1ms)

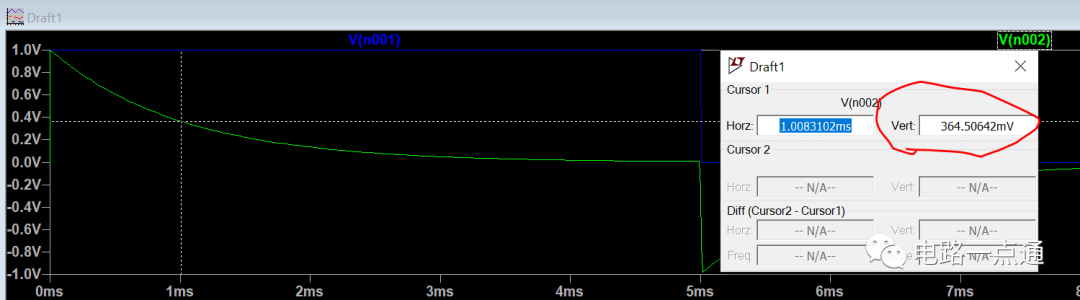
我们在图上实测一下：

总结

我们已经在本RC 微分器教程中看到，输入信号施加到电容器的一侧，输出信号跨接在电阻器上。 微分器电路用于为定时电路应用产生触发或尖峰脉冲。

当方波阶跃输入应用于此 RC 电路时，它会在输出端产生完全不同的波形。 输出波形的形状取决于输入方波的周期时间 T(因此频率为 ƒ)和电路的 RC 时间常数值。

当输入波形的周期时间也相似或短于(更高频率)电路 RC 时间常数时，输出波形类似于输入波形，即方波轮廓。 (关注公众号 电路一点通)当输入波形的周期时间远长于(较低频率)电路 RC 时间常数时，输出波形类似于窄的正尖峰和负尖峰。

输出端的正尖峰由输入方波的前沿产生，而输出端的负尖峰由输入方波的下降沿产生。 然后 RC 微分电路的输出取决于输入电压的变化率，因为效果与微分的数学函数非常相似。

审核编辑：汤梓红