一文了解RF噪声系数规范

仔细查看 RF 噪声系数的定义并讨论一些细微之处，以帮助避免对该规范的错误解释。

噪声系数定义和噪声因数方程

电路的噪声因数 (F) 可定义为：

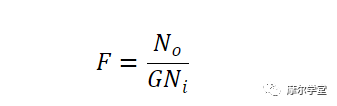
等式 1。

在哪里：

No 是输出端的总噪声，包括电路内部噪声源的影响和来自源阻抗的噪声

N i 是源阻抗在电路输入端产生的噪声

G是阶段的功率增益

虽然这个解释是正确的，而且实际上在一些参考资料中也提供了类似的解释，例如Paul R. Gray广泛使用的 教科书“模拟集成电路的分析与设计”第 4 版，但它并没有提供所有的细节噪声系数定义。根据IEEE 定义，N i 是源电阻器在 T 0  = 290 K°（或 16.85 °C）温度下的可用热噪声功率。这个温度比舒适的室温要低一点；但是，有时在 RF 工作中将其称为室温。

此外，IEEE 定义指出，No是 设备输出端的可用噪声功率，G 是设备的可用功率增益。这里的关键点是规范的参考温度 T 0  = 290 K°，以及用于描述方程式 N i、 N o和 G 的所有三个参数的描述符“可用”。在本文的其余部分，我们将详细讨论“T 0  = 290 K 时的可用噪声功率”的含义。

最大可用噪声功率

热激发电荷载流子的随机运动表现为电阻器中的噪声。噪声电阻器可以通过添加与无噪声电阻器串联的噪声电压源来建模，如下图 1 所示。

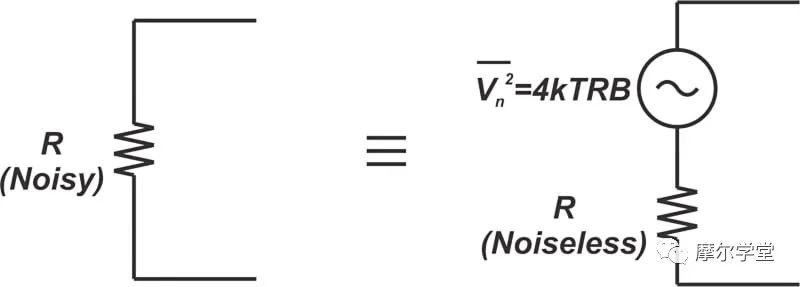
图 1. 噪声电阻示例图以及添加与无噪声电阻串联的噪声电压源。 

噪声电压源的PSD（功率谱密度）为¯¯¯¯¯¯¯V2n=4 kTRB��2个¯=4个 �吨�乙， 在哪里：

k 是玻尔兹曼常数 (1.38 × 10 -23  Joules/Kelvin)

T 是开尔文温度

B 是考虑的带宽（赫兹）

在噪声系数定义中，N i 是源电阻的最大可用噪声功率。现在的问题是，图 1(b) 中的电路可以提供的最大噪声功率是多少？根据基本电路理论，我们知道当负载电阻等于源电阻时传输的功率最大。因此，可以使用以下电路（图 2）找出源电阻 R S的最大可用噪声功率。 

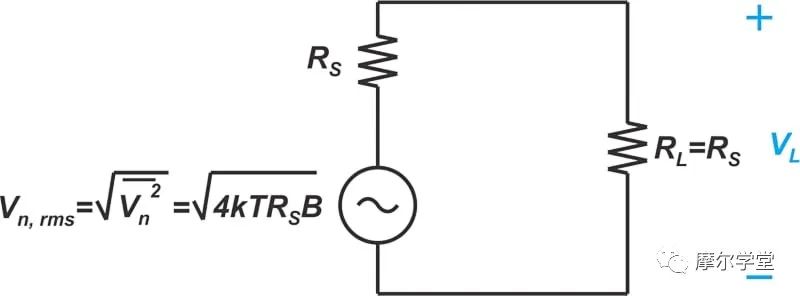
图 2. 用于查找源电阻器最大可用噪声功率的电路图。

请记住，我们 在上图中使用了噪声源的RMS（均方根）值。由于一半的噪声电压出现在负载两端，因此传输到匹配负载的噪声功率 R L  = R S可以通过以下公式找到：

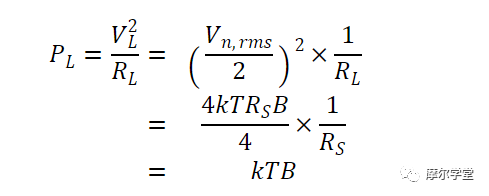
等式 2。

这是噪声系数计算的重要结果。请注意，可用噪声功率与电阻值无关。无论是 1 mΩ 电阻还是 1 MΩ 电阻，可用的噪声功率都是 kTB。在 1 Hz 带宽中，可用噪声功率为 kT。噪声系数定义基于 T 0  = 290 K 时的可用噪声功率 。以 dB表示 kT 0时，此参考温度下的可用噪声功率为 -174 dBm/Hz，计算如下：

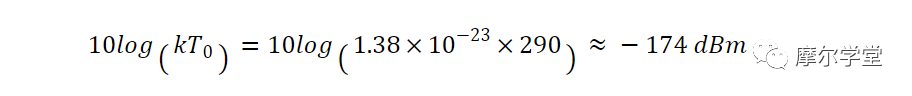
噪声系数指定添加噪声的相对量

由于噪声系数定义基于 N i  = kT 0 B，它指定了相对于 N i添加到信号中的噪声的相对

量。考虑我们在上一篇文章中推导出的以下噪声系数方程：

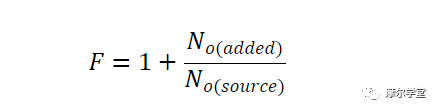
这里，No (source) 是源于源阻抗的输出噪声的一部分；No (added) 是电路本身产生的输出噪声的一部分——不包括源电阻贡献。注意 N o(source)  = kT 0 BG，我们得到等式 3：

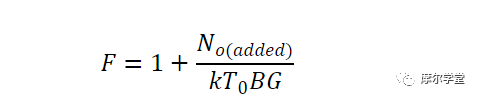
等式 3。

为了更好地形象化上述等式的噪声项，请考虑图 3 中的下图，有时称为“噪声线”。

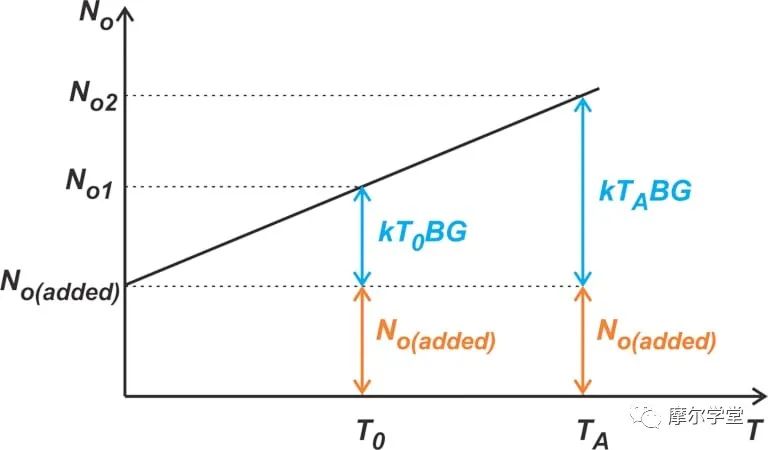
图 3. 显示噪声线的图。

在上图中，总输出噪声 No 相对于源电阻温度 T 绘制。如果 R S 无噪声（或 T = 0 K），输出端出现的唯一噪声将是被测设备或 No o(added)。当我们提高 R S的温度时，它的噪声贡献会增加。对应于 T = T 0的噪声系数度量实际上指定了 R S 在 T 0时贡献的输出噪声（即 kT 0 BG）与被测设备的输出噪声 (No (added) ) 之比。例如，如果系统的噪声系数为 F = 2（或 NF = 3 dB），我们知道 No (added) 等于 kT 0 BG。

如图所示，R S 噪声与 No (added)的比值 不是常数，而是随 T 而变化。因此，如果 R S 处于 T 0以外的温度，我们不能直接使用噪声系数方程来计算找到输出噪声。 相反，我们应该首先找到来自 DUT（被测设备）的噪声，加上感兴趣温度下 来自 R S的噪声，最后计算总输出噪声。

我们还可以通过将分数的分子和分母除以级的功率增益，根据输入参考噪声值来表达等式 3。这产生了等式 4：

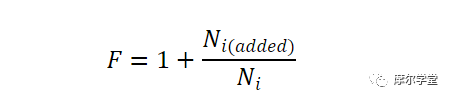
等式 4。

在这个等式中，N i(added) 是由 DUT 贡献的输入参考噪声，N i 是源在 290 K 时的可用噪声功率。同样，如果 F = 2，则输入参考噪声由DUT 等于 N i  = kT 0 B。让我们看一个例子来阐明这些概念。

示例：使用噪声系数方程

放大器的噪声系数、带宽和增益分别为：

噪声系数 = 2.55 分贝 

B = 10 兆赫

增益 = 5.97 分贝

假设可用输入噪声为 kT A B，找出两种不同情况下的输出噪声：1 - T A  = 290 K 和 2 - T A  = 150 K。 

我们首先找到噪声系数和增益的线性值： 

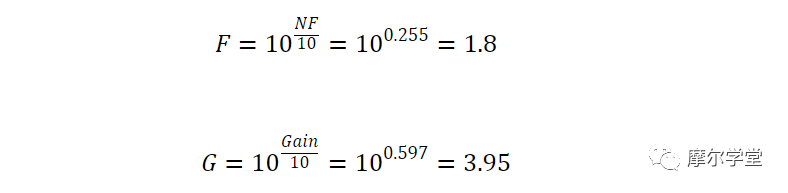
由于噪声系数的定义假设输入噪声是 T = 290 K 时的可用噪声功率，我们可以直接从等式 1 求出该温度下的输出噪声：

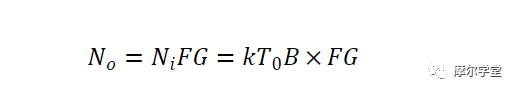
以分贝表示右侧，我们有：

对于 T A  = 150 K，我们不能直接使用噪声系数方程。然而，噪声系数方程可用于计算系统产生的噪声。将 N i  = kT 0 B 代入等式 4，系统产生的输入参考噪声为： 

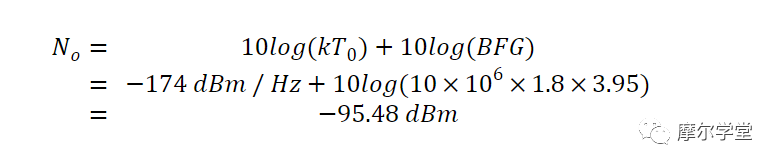
将该值乘以系统增益 G，即可得到总输出噪声功率。在下面的等式中，我将 T A写成 T 0 以简化计算：

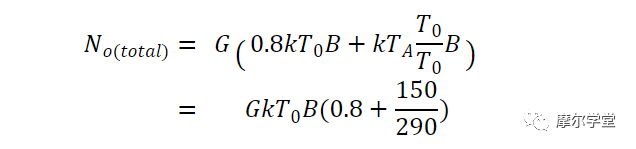
以分贝表示右侧，我们有：

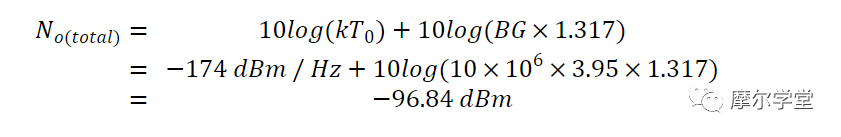
如果不注意噪声系数的定义，可能会将 N i  = k × 150 × B 代入等式 1，这会产生不正确的结果 No =  -98.34 dBm。 

物理温度或噪音温度

在上面的讨论中，我们强调了源电阻 R S的物理温度对我们的 NF 计算的影响。通常情况下，驱动点阻抗 (R S ) 与 DUT 处于相同的物理温度；然而，电路接收到的输入噪声功率高于 kT 0 B。这通常发生在级联系统中，信号链中的每个模块都会增加本底噪声。因此，级联中下游级的输入噪声通常超过 kT 0 B。在这些情况下，我们也无法通过直接应用噪声系数方程来计算输出噪声电平。相反，我们可以先使用 NF 方程来计算电路产生的噪声 (N i(added))，然后使用该信息和输入噪声电平来计算总输出噪声。 此外，定义输入噪声的等效噪声温度 T e也很有帮助。这是可用热噪声功率 (kT e B) 等于输入噪声功率时的温度。若输入噪声功率为N 1，其等效噪声温度为：

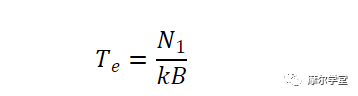
噪声系数和等效噪声温度是组件噪声特性的可互换表征。在下一篇文章中，我们将查看使用噪声温度概念的示例。

噪声系数指定 SNR 劣化

噪声系数是电路引起的SNR（信噪比）退化的直接量度。这个说法是正确的；然而，它值得更多的解释。让我们再考虑一次上面讨论的例子。我们假设系统的噪声系数和增益分别为 NF = 2.55 dB 和增益 = 5.97 dB，并假设输入信号功率为 -40 dBm。当 R S 为 T A  = 290 K 时，输入噪声功率为： 

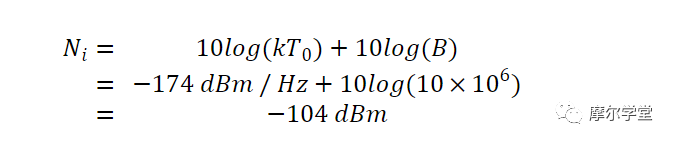
从示例的结果中，我们知道输出噪声功率为 -95.48 dBm。图 4 总结了该示例输入和输出端的信号和噪声功率。

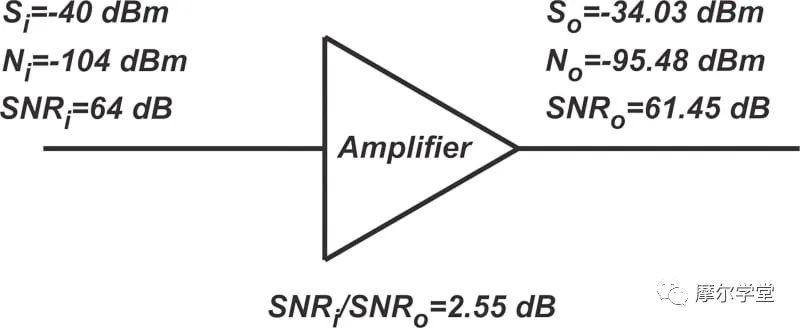
图 4. 前面示例的输入和输出端的信号和噪声功率汇总。

输出信号功率由输入信号乘以放大器的功率增益得到。图 4 还提供了输入和输出 SNR，以及 SNR 退化。请注意，SNR i  / SNR o的比值 等于噪声系数 NF = 2.55 dB，这并不奇怪，因为我们知道这个比值实际上是噪声系数的定义。但是，对于 T A  = 150 K的情况呢？在这种情况下，输入噪声为 N i  = -106.86 dBm。图 5 总结了前面示例的结果。

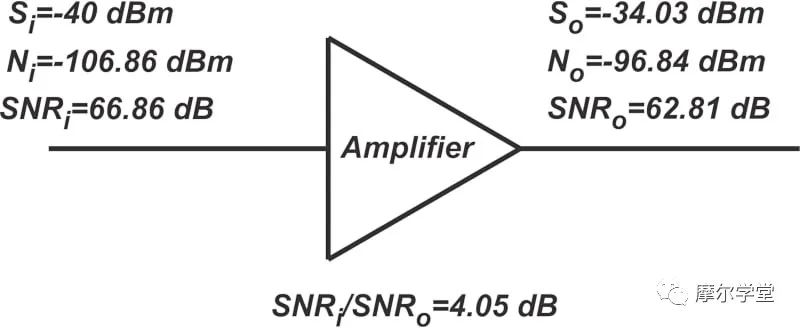
图 5. 上述示例的另一个结果汇总。

如您所见，SNR 退化 (SNR i  / SNR o ) 现在大于 NF。这是因为输入噪声低于标准值，使得放大器的噪声贡献更加显着。因此，当输入噪声为 kT 0 B时，噪声系数决定了 SNR 的退化。例如，如果一个电路的噪声系数为 7 dB，并且该模块的输入噪声功率为 kT o B，则输出端的 SNR该块的 7 dB 小于输入 SNR。

彩蛋来了

从基础到高级的ADC讲座，将涵盖高速ADC设计的原理、传统架构和最先进的设计。第一部分首先回顾了ADC的基本知识，包括采样、开关电容和量化理论。接下来，介绍了经典ADC架构的基础和设计实例，如闪存、SAR和流水线ADC。然后，本教程将对混合型ADC架构进行总体概述，这就结束了第一部分。在第二部分，首先描述了ADC的度量。然后，介绍混合或非混合架构的各种先进设计。该教程最后将以数字辅助解决技术结束。

审核编辑：汤梓红