点到点ICP做对了也能实现简单准确且鲁棒的激光里程计

1 动机与贡献

现有很多LiDAR里程计都依赖于某种形式的ICP估计帧间位姿，例如CT-ICP, LOAM等。现有的系统设计需要对机器人的运动(CT-ICP)和环境的结构(LeGO-LOAM)有一些特定的假设。而且几乎没有系统能够不需要调参（例如特征提取、面特征拟合、法向量估计、畸变矫正）就能用于不同的场景、不同的LiDAR、不同的运动模式、以及不同种类的机器人（例如地面和空中机器人）。

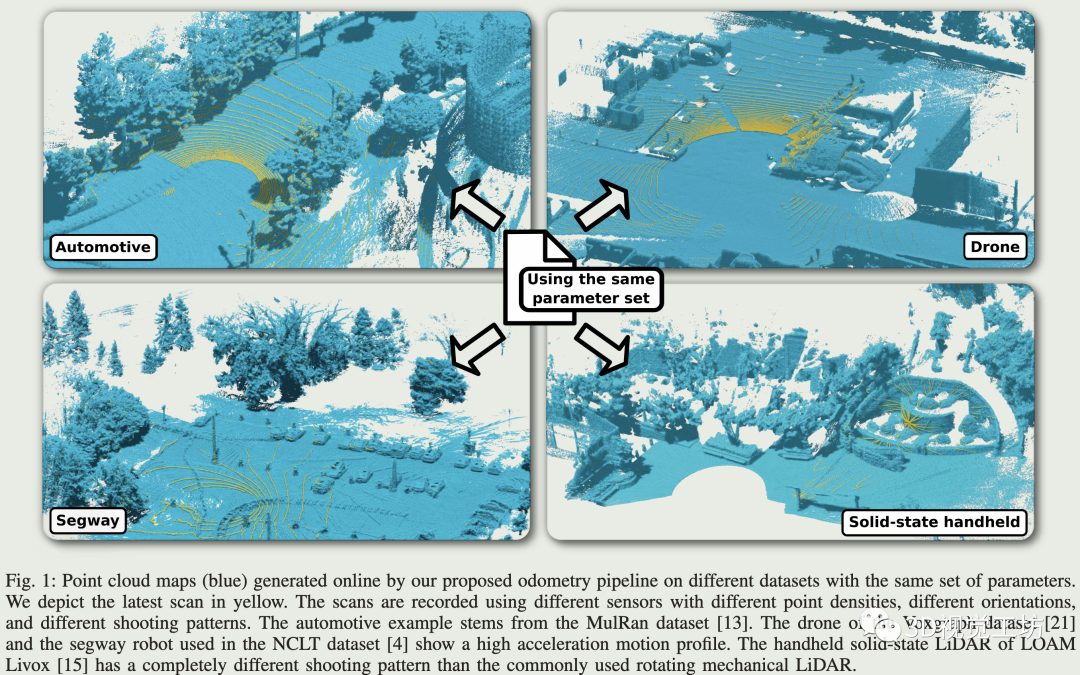
与现有很多工作增加里程计的复杂度相反，本文通过去除大部分部件并专注于核心元素，回顾1992年最初提出的ICP方法，研究阻碍其泛化性能的根本原因，得到了一个简单且非常高效的系统，并且可以使用不同的LiDAR传感器在各种环境条件下运行（无人车、无人机、两轮车Segway、手持固态LiDAR）。

提出的里程计估计方法基于point-to-point ICP，结合了自适应阈值进行对应匹配、鲁棒核、简单但广泛适用的运动补偿方法和点云下采样策略。 和现有很多SLAM系统不同，本文的系统不用精巧的特征提取，学习方法，也不用回环检测。

整个系统参数较少，在大多数情况下甚至不需要调整到特定的LiDAR传感器。 不需要集成IMU信息，只需要从各种3D LiDAR传感器获得的3D点云数据，因此能够满足广泛的不同应用和操作条件。 系统运行速度比所有数据集中的传感器帧率都快，并且是为现实场景而设计的。 KISS-ICP (keep it small and simple):

与SOTA里程计系统相当

同一套参数可以用于不同的机器人、不同的环境和运动模式

不依赖IMU或轮速计的高效运动补偿方法

2 方法

激光里程计主要步骤：

运动估计和运动补偿（畸变矫正）

帧下采样

使用自适应阈值估计scan到local map的对应关系，对可能的数据关联做限制，滤除可能的异常值

用鲁棒的point-to-point ICP进行scan与local map的配准

将下采样的scan更新到local map中

2.1 运动预测和帧畸变矫正

不使用IMU或轮速计，用恒速模型进行运动补偿，主要有两个原因：

应用广泛，不需要其他传感器，也就不需要和其他传感器做时间同步

对于获得LO的初始值和畸变矫正足够了，因为通常LiDAR频率在10Hz到20Hz（50ms~100ms），大多数情况下，加速度或者减速度在短时间内与恒速模型的差距相对较小

用前两帧的相对位姿预测当前帧与前一帧的相对位姿，t-1到t-2的相对位姿为：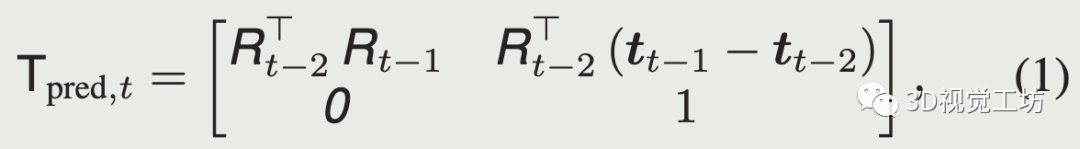



速度和角速度：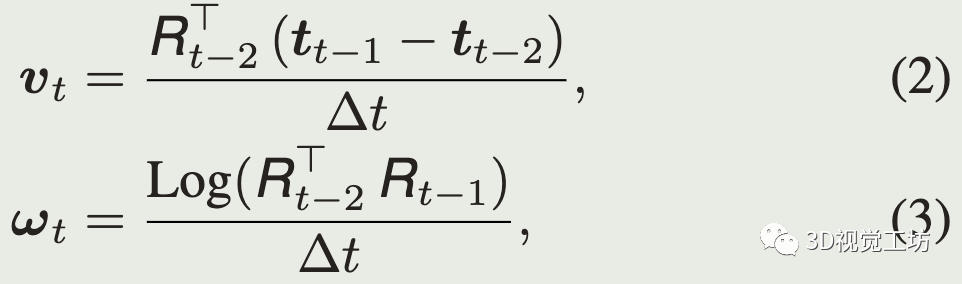



畸变矫正（投影到扫描开始）：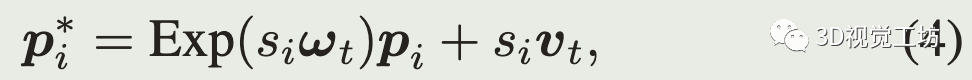



2.2 点云下采样

local map的voxel 大小是v，对于scan，先用alpha * v (0 < alpha <= v)的voxel大小进行下采样, 然后 用beta * v (1.0 <= beta <= 2.0)的voxel大小进行下采样，两次下采样的想法源于CT-ICP。 大多数体素下采样方法保留voxel的中心点，不一定位于原点云上，本文实验发现保留原点云的点效果要好一点，因此在实现中，保留第一个插入voxel里的点。

2.3 自适应阈值的scan到local map对应关系估计

用大小为v的voxel存储局部地图，每个voxel最多存N_max个点，scan配准到local map后，用估计的位姿将上述第一次下采样的点云加入到local map中，如果voxel超过了传感器最大距离r_max, 就从local map去除。 一般ICP方法都用某一最大距离范围（例如1m或2m）内的最近邻做数据关联，这个阈值的确定需要考虑初始位姿误差、动态物体种类和数量、以及传感器噪声等，通常是根据经验设定的。

基于恒速运动预测模型，可以估计运动估计的初值与ICP纠正的偏差大小，但这个是不能提前知道的。直观地，可以观察机器人在该偏差上的大小的加速度，如果机器人没有加速，该偏差的大小会很小，接近0，ICP基本不需要做纠正。 将该信息集成到数据关联中，估计两帧之间关联点的距离：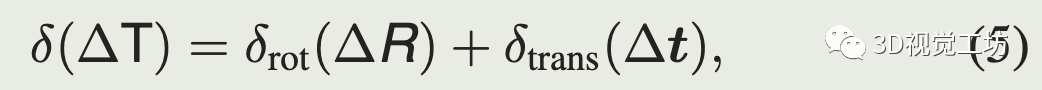



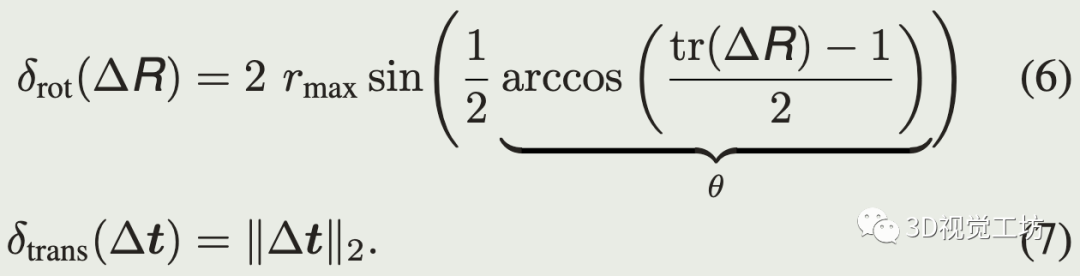
旋转部分的偏差对应在扫描最大距离上偏差的大小。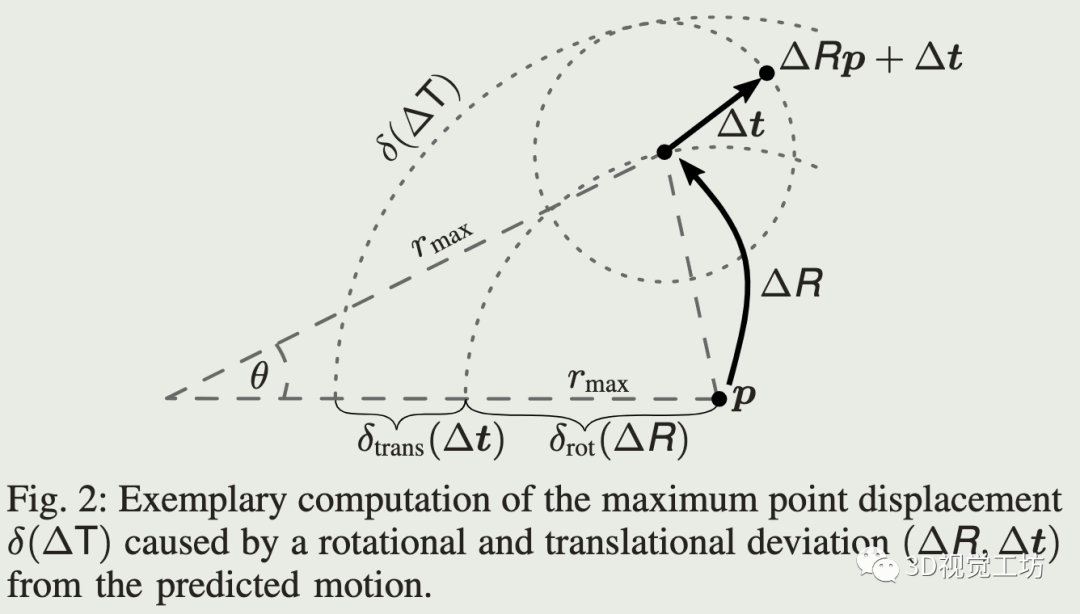



式（5）给出了点偏差的上界（根据三角不等式）：



为了计算t时刻的阈值，假设式（5）的值服从高斯分布，根据已有的轨迹，只考虑当偏差大于delta_min（恒速运动和真实运动相差较大）时，得到标准差：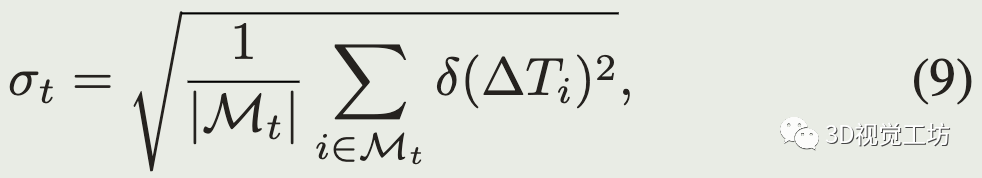



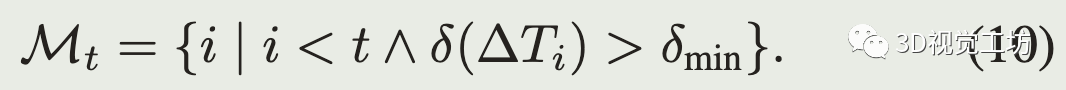
只考虑偏差大于delta_min避免了由于机器人静止或者匀速运动很长时间使得标准差估计得太小。实验中将delta_min设为0.1m。最后估计的阈值设为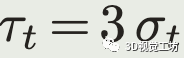



用于数据关联的最近邻搜索时的距离阈值。

2.4 通过鲁棒优化配准

先通过预测的相对位姿和上一帧的里程计位姿把点云转到全局坐标系（也可以是局部子图坐标系）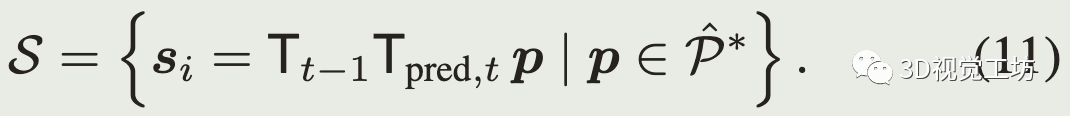



每次迭代时，点到点残差做ICP配准的优化问题为：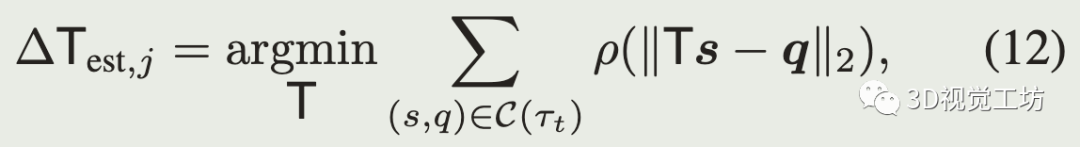



rho是Geman-McClure鲁棒核函数，一种具有很强的外点剔除能力的M估计器: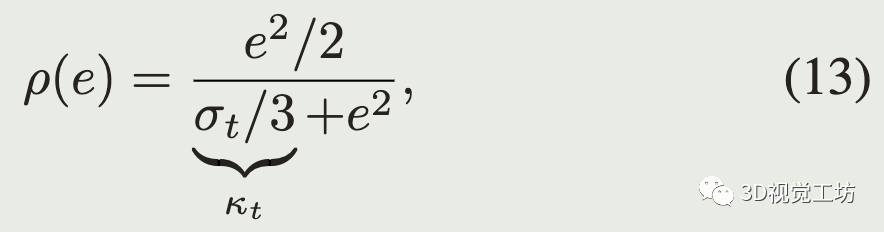



第j步迭代完后更新点云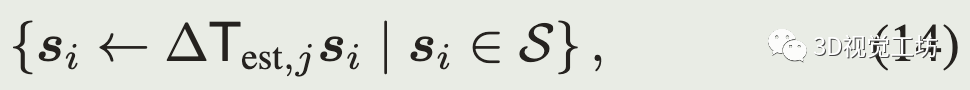



然后重复迭代数据关联、优化，直到满足收敛条件。 最后里程计的位姿为：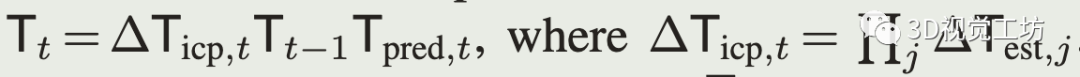



式（5）中运动预测和ICP纠正之间的相对位姿为：



通常ICP会设定一个最大迭代次数，或者加上迭代结果与最小变化量的比较，本文认为限制这些约束可能使ICP不一定能收敛到好的结果，而且可能会累积漂移。

因此，本文的终止条件为迭代结果小于gamma，而限制迭代次数。 最后用ICP纠正后的位姿将第一次下采样的帧加入到local map。

算法的参数设定：



r_max依赖于传感器种类。

3 实验

公开数据集对比：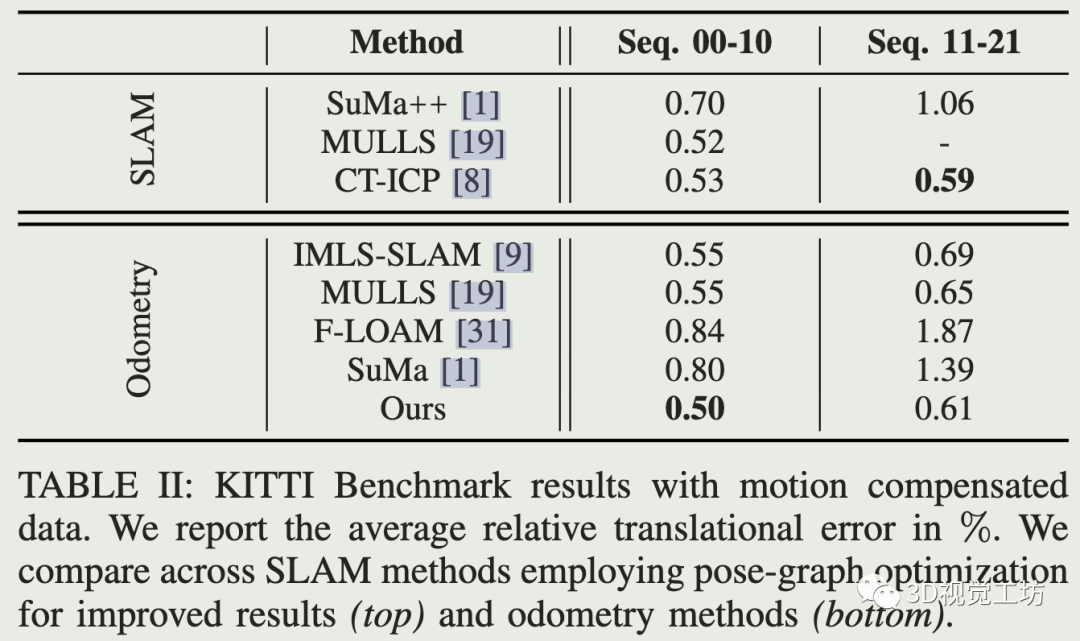



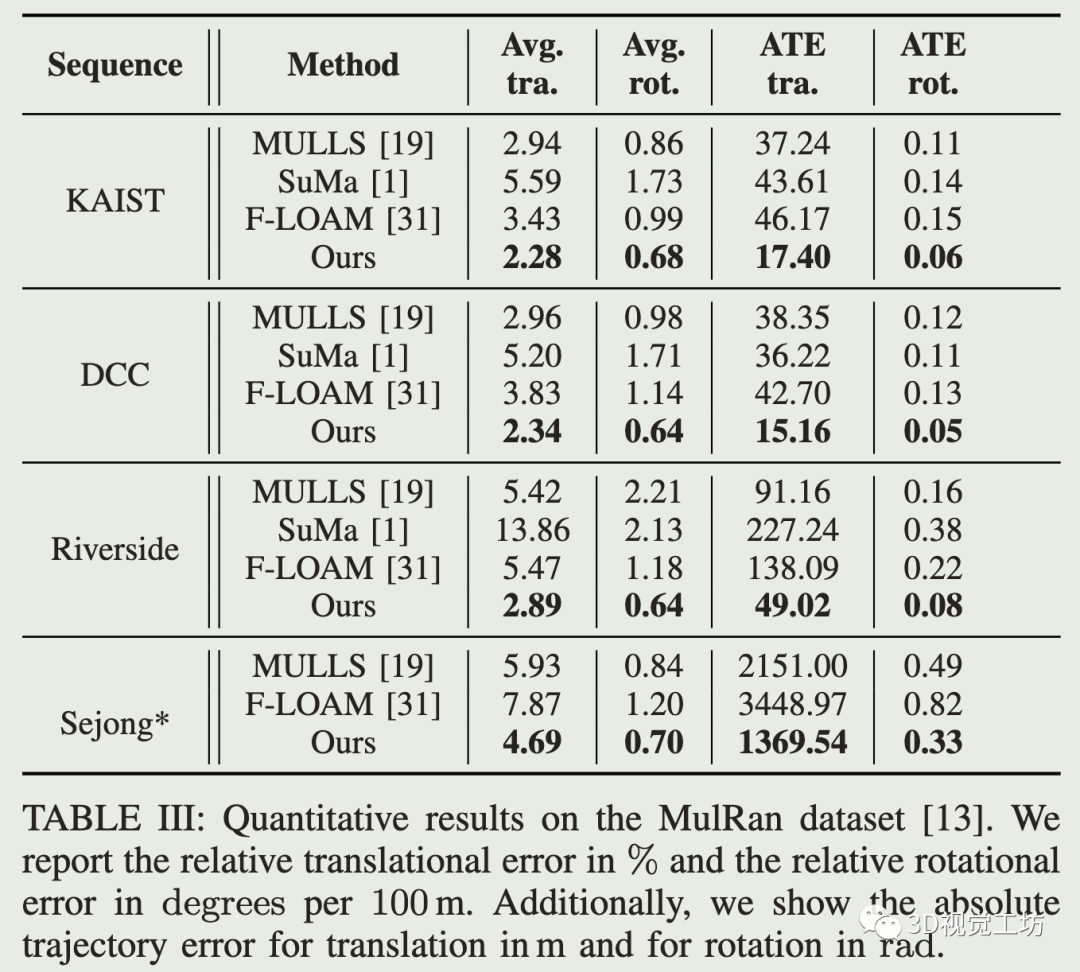
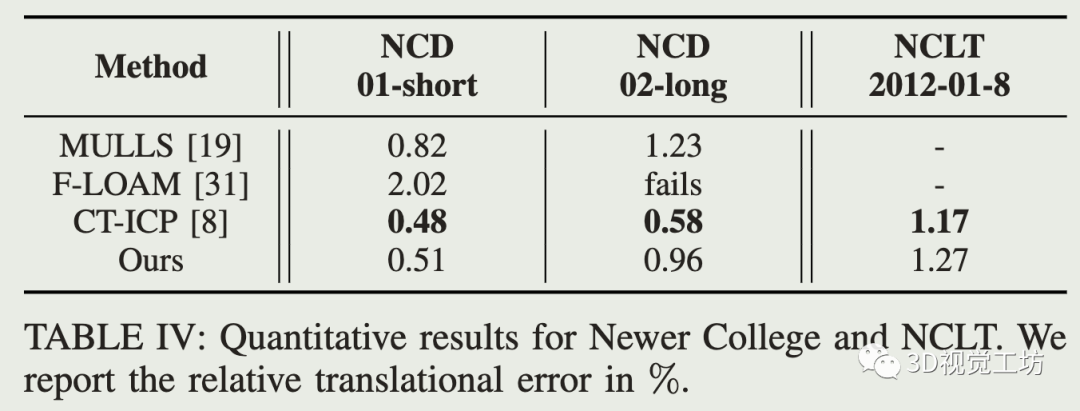
运动补偿：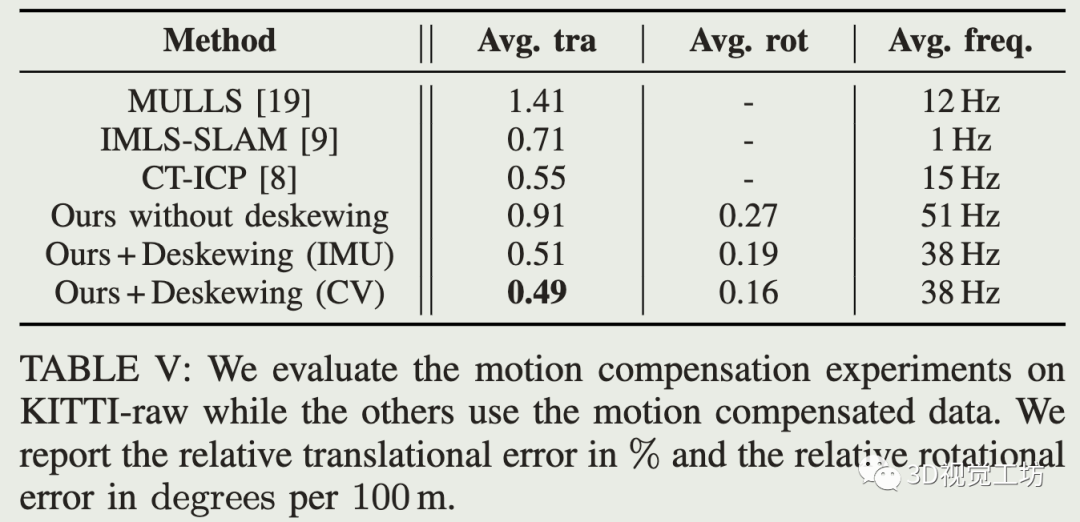



自适应数据关联阈值：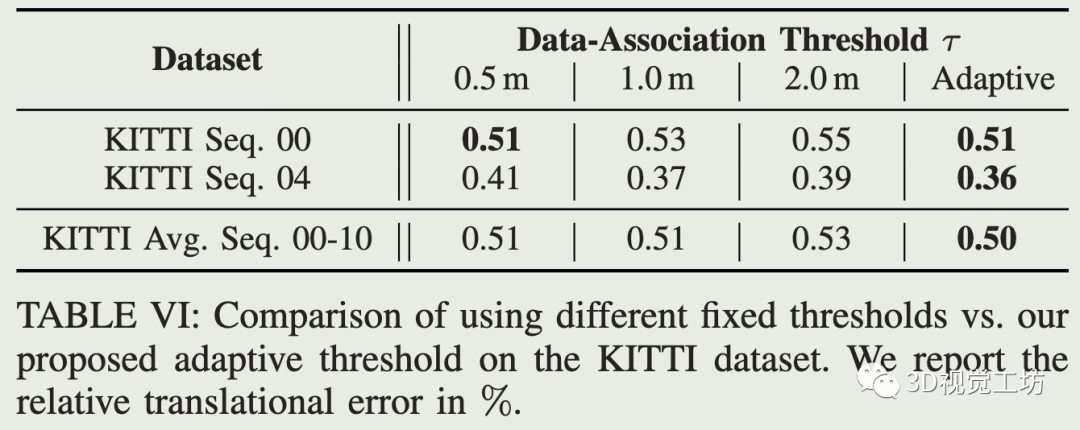

审核编辑：刘清