

用于二维近场微波和毫米波SAR图像重建的多频CS模型介绍
电子说
描述
概述
本文研究了一种新的二维近场微波毫米波合成孔径雷达(SAR)成像系统多频压缩传感(CS)模型,该模型通常收集多频稀疏数据。每个频率的空间数据在小波基下表示为分层树结构,不同频率的空间数据被建模为联合结构,因为它们高度相关。基于所开发的多频CS模型,利用频率内和频率间的相关性,提出了一种新的CS方法,并丰富了现有的CS方法,用于欠采样测量的二维近场微波和毫米波SAR图像重建。将拆分布雷格曼更新与平行快速迭代收缩阈值算法近端算法的变体相结合,所提出的CS方法最小化了五个项的线性组合:最小二乘数据拟合,多L数据拟合1范数,多总变异范数,关节稀疏性l21范数和树稀疏性重叠 l21规范。仿真和实验结果表明,所提方法在效率和收敛速度方面均具有优异的性能。
第一节.
雷达成像是一种逆散射问题,其中电磁信号脉冲被传输到场景,并通过散射电场的测量重建反射率的空间图。合成孔径雷达(SAR)成像系统通常与移动天线探头一起运行,该探头以高带宽和高空间分辨率对目标场景进行采样,如果根据香农-奈奎斯特定理重建图像,则需要在频域和空间域中实现高采样率。然而,压缩感知(CS)的最新进展将SAR图像重建视为为一组未确定的线性方程找到稀疏解,该方程能够生成测量值低于Nyquest采样率的高分辨率图像。CS-SAR方法已成功应用于各种远场应用,这些应用通常从移动平台(如飞机或卫星)生成静止表面目标和地形的高空间分辨率图像。例如提出了一种匹配滤波的替代方案,通过使用正则化正交匹配追踪算法实现方位角压缩,用于检索被照亮的场景。使用范数优化来降低方位方向的采样率。 基于贝叶斯CS实现距离和方位角压缩采样,这需要对传统的SAR系统进行微小的更改。此外,CS还应用于其他远场应用,例如逆SAR和层析SAR。
相比之下,近场雷达成像通常在比远场场景相对较近的距离内工作,并且在图像重建中考虑了波前曲率。当在高频下运行时,近场SAR成像系统由于其波长小,可以实现高空间分辨率。成熟的微波频谱范围约为300 MHz至30 GHz,而30-300 GHz的频率跨度与毫米波频谱相关;相应的波长范围分别为1 000–10 mm和10–1 mm。近场微波和毫米波成像系统结合了成像技术,如透镜聚焦和近场校正技术,在各种测试和监测应用中将分辨率提高到毫米级。值得注意的是,入射波和散射波的干扰是由于目标表面粗糙而发生的,并且取决于被测试样(SUT)的几何形状。与远场SAR应用相比,通过对照亮SUT的信号施加相当大的带宽,在近场应用中,这种干扰引起的散斑噪声和几何畸变大大降低,并且散斑噪声和几何畸变随着信号带宽的增加而逐渐消失。在我们的应用中,我们使用了如此宽的频段,因此斑点噪声和几何畸变不是问题。
用于无损检测和评估(NDT&E)的近场微波和毫米波成像技术,为了对SUT进行成像,使用宽带微波或毫米波穿透介电材料并与SUT的内部结构相互作用。来自SUT的反射散射体由接收器采集,并处理接收到的反射系数以呈现全面的图像以供检查。近场SAR成像系统通常使用收发器天线使用精密自动扫描仪在统一的二维测量网格上对SUT进行光栅扫描,并且沿孔径所需的采样率由许多因素决定,包括波长,孔径大小,目标大小以及与目标的距离传统的均匀采样需要采样空间来满足奈奎斯特采样标准,即使是合理大小的SUT ,所需的测量点总数通常也很大。这些SAR成像系统的数据采集速度较慢,阻碍了其实际应用。最近开发的CS技术通过在均匀网格上随机采样一小部分空间点并大大减少数据采集时间,显示出有希望的结果。实验表明,只要空间点的数量保持不变,多频测量就会使用相同的扫描时间,因此多频测量通常用于2D图像和3D图像。
在一些NDT&E应用中,目标的2D图像是足够的或优选的,然后从多个频率重建的2D图像只需通过传统的CS模型平均以减少噪声。该方法的下划线假设是频率测量是独立的,CS算法仅利用恢复图像的标准稀疏性,然而,这种传统的CS恢复过程仍然需要高比例的空间采样点,有时会受到大量噪声、多重反射、色散或偏振变化等的影响。
很明显,多频测量表现出频率内和频率间的相关性。本文介绍了一种新的多频CS模型,该模型同时利用了多频测量的树稀疏性和联合稀疏性的相关性。树稀疏性已经成功地用于压缩成像。多频SAR图像在小波域中近似树稀疏,这意味着,如果树上的节点为非零,则导致根的所有祖先通常也是非零的。关节稀疏性是在多测量向量(MMV)问题中提出的群稀疏性结构的一个有趣的特例,例如多通道压缩传感和医学成像。联合结构意味着不同频率的SAR测量系数共享一个共同的非零支撑。通过将树稀疏性和关节稀疏性与标准稀疏性相结合,提出的新型多频CS模型使我们能够进一步减少恢复目标SAR图像所需的测量次数,并更好地区分真实信号信息和伪影。
基于引入的多频CS模型,二维SAR图像重建问题成为一个约束最小化问题。我们采用拆分布雷格曼框架将这个约束最小化问题转换为一系列无约束问题,这些问题最小化了两个项的线性组合。一个项是最小二乘数据拟合,另一个项是反映先验的惩罚函数。这个新 CS 模型的惩罚函数包含一个范数、一个多电视范数、一个联合稀疏性范数和一个树稀疏性重叠的范数。由于复合结构复杂,该惩罚函数导致难以解决的无约束最小化问题,无法通过传统的近端分裂方法有效解决,如正向-后向(FB)分裂算法、道格拉斯-雷奇福德分裂算法、乘数交替方向法、乘数同时方向法和广义FB分裂算法。
在本文中的其余部分,我们首先介绍近场SAR的基础知识和2-D近场SAR成像系统的CS方法。接下来,我们描述了所提出的多频CS模型和相应的CS最小化,以利用SAR数据的频率内和频率间数据相关性。我们还讨论了多种稀疏模式的权重选择及其对性能的影响。最后,给出了利用所提多频CS模型的仿真和实验结果,并与4个实例进行了对比。所提出的多频CS-SAR方法在使用比现有方法更低的欠采样率的同时实现了更高的重建图像质量。
第二节.多频压缩感知模型
A. 二维近场SAR成像系统
考虑一个宽带微波或毫米波SAR成像系统,该系统在XYZ笛卡尔空间中检查SUT,其中具有特定波束宽度的收发器天线在SUT上以一定距离进行光栅扫描。
值得注意的是,波的振幅衰减与范围无关,因为它对聚焦图像几乎没有影响。近场SAR成像系统还假设目标只有一个反射,并且假设目标是平坦的,与扫描平面平行。通过多频测量,可以重建目标的3D图像和2D图像。在一些NDT&E应用中,目标的2D图像对于检测SUT是足够的或首选的。多频测量通常需要矢量网络分析仪,它可以非常快速地扫描等距角频率。因此,减少频率点的数量并不能节省我们应用中的采集时间,尽管它在其他一些雷达应用中很重要且很有价值,例如探地雷达。另一方面,减少二维空间扫描区域的采样点数量对缩短采集时间起着重要作用。
虽然单频测量足以重建二维图像,但多频测量比单频测量可以形成更好的目标二维图像。此外,采用完善的CS方法的多频测量可以进一步减少测量/采样点,从而节省采集时间。利用多频测量的内在结构/稀疏性,开发合适的CS方法进行二维近场SAR图像重建具有重要意义。
B. 二维SAR成像系统的压缩传感
CS引入了一种新的信号采集框架,该框架使用一组固定的线性测量和非线性恢复过程,并超越了传统的奈奎斯特采样范式[4]。CS方法强调重建过程中估计图像与实际收集的原始测量值之间的一致性。对于SAR成像系统的每次频率测量,恢复图像的大小波系数倾向于生活在有根的,连接的树结构上,称为树稀疏性。对于SAR成像系统的多频测量,不同频率测量的系数共享相同的支撑,这称为联合稀疏性。我们探讨了结构依赖的树稀疏性和联合稀疏性,并引入了一种新的多频CS模型,通过将它们集成在一起进行二维SAR图像重建
关节稀疏性是一种特殊的非重叠群稀疏性,在MMV问题中提出。对于二维近场SAR成像系统,在不同频率下重建的SUT的二维图像具有相同的稀疏性模式。换句话说,2-D SAR图像集的有效系数位于相同的位置。多频测量二维SAR成像系统的联合稀疏解,即一组稀疏解,共享一个共同的非零支撑。为了获得更好的最佳分辨率和图像质量,SAR成像系统通常需要多频测量,并且对于微波和毫米波SAR系统而言,采集间隔尤其严格。由于噪声和SAR系统的限制,从单频测量中恢复的图像通常比从多频测量中恢复的图像遭受更多的阴影和伪影。为了进一步提高恢复图像的质量并减少采样点的数量,这个新的CS模型不仅利用了多频测量中的联合稀疏性,还利用了每个频率测量中的树稀疏性和标准稀疏性($ell _{41}$规范和电视规范)。通过这种新的多频CS模型,第三节中提出的CS方法可以通过利用更现实的SAR模型来大幅降低欠采样率,该模型超越了简单的稀疏性和可压缩性,并包括信号系数的值和位置之间的结构依赖性。
第三节.多频模型的压缩感知建议
在重建过程中具有良好的数值稳定性,分裂布雷格曼框架被证明在处理噪声测量方面是有效的。使用分裂布雷格曼框架,约束问题可以转换为一系列无约束问题。并行 Dykstra 类近端算法使用并行算子拆分结构,将复杂的最小化问题转变为几个更容易的邻近问题。当将此算法嵌套在求解的迭代中时,这将需要多次迭代才能接近最佳结果,并导致计算复杂度的大幅增加。为了加速收敛进程,通过将类FISTA更新阶段与并行算子拆分结构集成,引入类似FISTA的并行近端算法,如算法2所示。类似 FISTA 的更新步骤在根据前两次迭代和显式动态更新步长专门构造的辅助点进行评估,并使类似 FISTA 的并行近端算法收敛,通过使用我们的数值实验所证明的这一更新步骤,III-B节中提出的CS方法大大加快了速度。
所提出的CS方法使用分裂布雷格曼更新和并行FISTA类近端算法的变体来近似问题的最优结果。通过数值实验所证明的类似FISTA的更新阶段,所提出的CS方法大大加快了速度。采用TVL1、TVL1Tree和TVL1Joint三种不同的模型来验证所提出的多频CS模型的优越性能。通过同时考虑该多频CS模型中的树稀疏性和关节稀疏性,我们期望所提出的CS方法可以进一步减少稳定恢复图像所需的测量次数,并更好地区分信号恢复中的真实图像信息与恢复伪影。
第四节.模拟和实验评估
通过一组模拟、一组漆下腐蚀实验和一组骨料实验验证了所提CS方法的性能。为了证明所提出的CS方法的效率,使用2-D结构相似性(SSIM)指数进行2-D图像质量评估,并且它被认为比峰值信噪比(SNR)或均方误差更符合人眼感知。将从欠采样SAR测量中恢复的重建图像与从完全采样的原始数据中恢复的重建图像进行比较。如果重建的图像与完整的数据重建图像完全相同,则SSIM将为1。换句话说,较大的SSIM指数对应于更好的重建质量,反之亦然。为了证明所提出的多频CS模型的优越性能,使用图1(a)所示的完全采样原始测量中恢复图像的平均值作为真实图像,以比较不同模型,不同SNR和不同欠采样率的不同恢复图像。
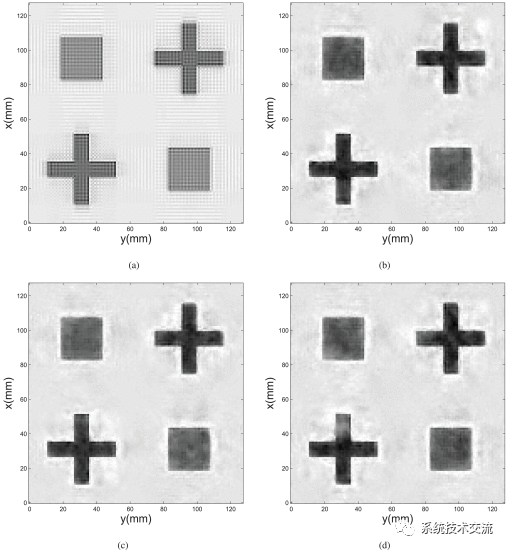
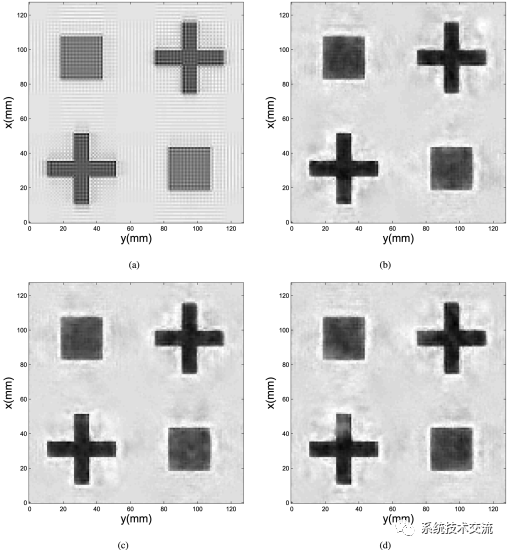
在欠采样率η=9%的情况下,在仿真原始数据中添加不同级别的噪声(不同的信噪比),图2(b)–(d)显示了使用相应CS方法与所提出的多频模型相关的恢复图像,证明了所提出的多频CS模型与相应的CS方法在处理噪声测量方面特别有用。
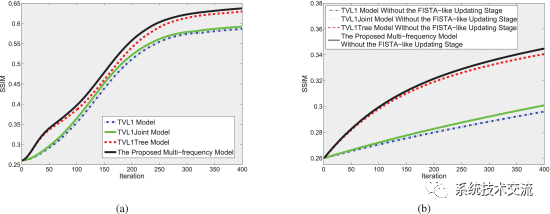
欠采样率η=10%时,不同模型和不同信噪比迭代期间恢复图像的SSIM收敛如图3(a)、(c)和(e)所示。在相同的欠采样率下,表明所提出的多频CS模型可以实现比其他1种模型更大的SSIM值。对于仅考虑多频测量的标准稀疏性的SAR成像的传统方式,TVL1模型实现的SSIM远低于其他模型,TVL1模型恢复的图像明显存在更多的阴影和伪影。考虑到树稀疏性,TVL1Tree模型恢复图像的SSIM比TVL1模型恢复的图像更好。此外,考虑到多频测量的高度相关结构(关节稀疏性),TVL1Joint模型的恢复图像略优于TVL2模型的恢复图像。毫不奇怪,在利用树稀疏性和联合稀疏性的情况下,所提出的多频模型与基于TVL1、TVL1Tree或TVL1Joint模型的CS方法相比,具有相关CS方法的2D图像具有更好的分辨率和更少的背景噪声。
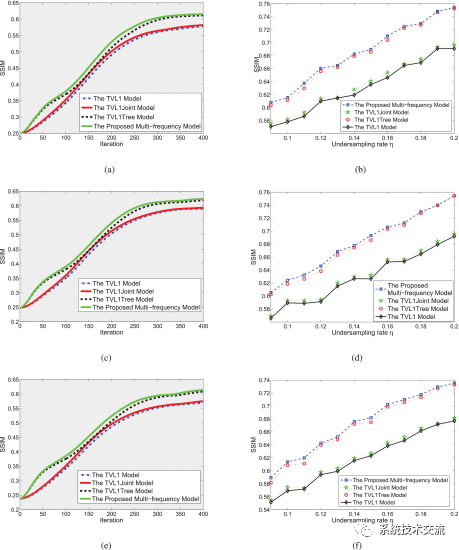
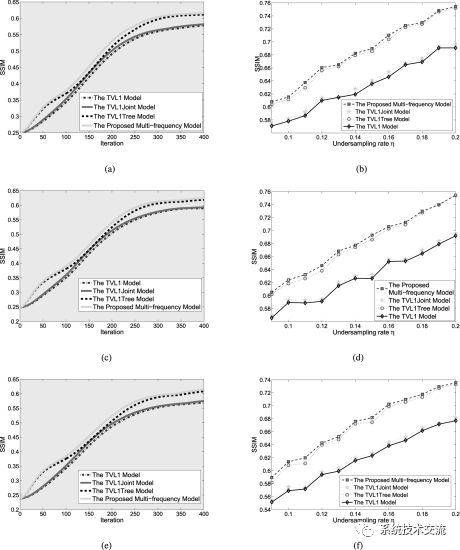
欠采样率从η=9%∼20%,步长为1%,在图3(b)、(d)和(f)下,将所提出的CS方法应用于不同SNR下的四种不同模型所获得的SSIM值。对于额外的结构化稀疏性信息,使用相关CS方法提出的多频CS模型实现了最佳的恢复图像质量。而且,很容易看出,所提出的多频模型仅比TVL1Tree模型略好。显示了应用于四个模型的SSIM收敛,无论是否使用类似FISTA的更新阶段。很明显,在相同的迭代中,使用类似FISTA的更新阶段的CS方法比不使用类似FISTA的更新阶段获得了更高的SSIM值。此外,证明了FISTA类更新阶段大大加速了所提出的CS方法,并使得所提出的CS方法具有较快的收敛速度。
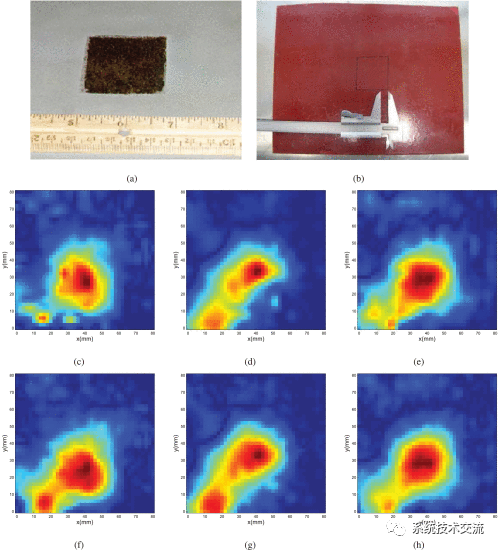


聚合示例:(a)第一次扫描实验,用TVL1模型在欠采样率η=35%下重建图像,达到SSIM = 0.7308。(b)第二次扫描实验,在欠采样率η=1%下用TVL35模型重建图像,达到SSIM = 0.7277。(c)第一次扫描实验,在欠采样率η=35%下,用提出的多频模型重建图像,达到SSIM = 0.7439。(d)第二次扫描实验,在欠采样率η=35%下,用提出的多频模型重建图像,得到SSIM = 0.7369。
当欠采样率从η=10%∼30%,步长为2%时,将所提出的CS方法应用于这些聚集体实验所获得的SSIM值如图8所示。随着欠采样率 η 的增加,实现的 SSIM 值逐渐增加。传统模型(TVL1模型)仅考虑恢复的SAR图像在稀疏域和梯度域中的标准稀疏性。相比之下,在额外的结构信息下,所提出的使用相关CS方法的多频CS模型比传统模型(TVL1模型)获得了更好的恢复图像质量。
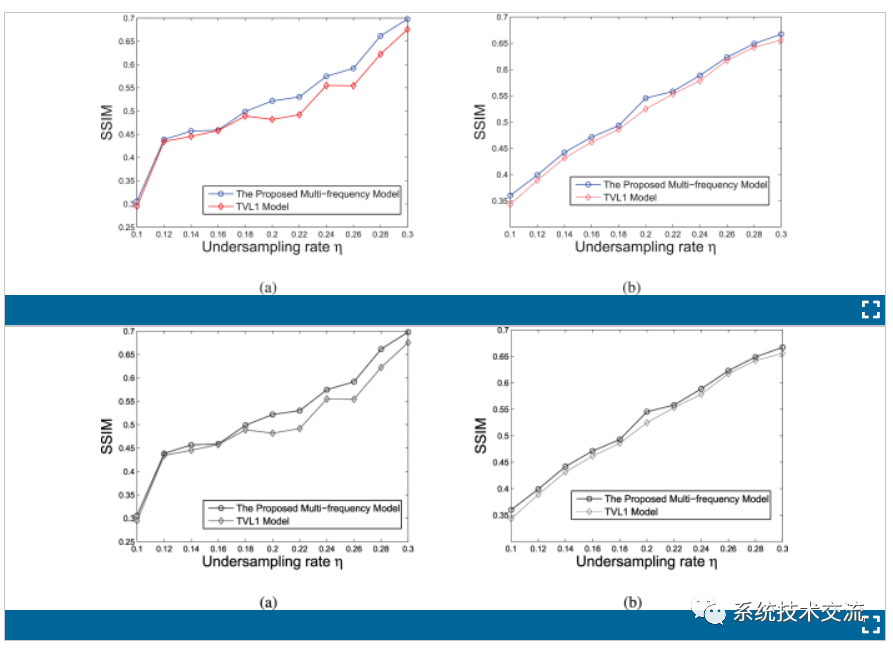
这些聚集体实例存在背景噪声大、目标多重反射以及SAR系统受限等限制,如孔径有限、天线波束宽度受限等。这些限制使得在这些聚集体示例中提出的多频CS模型中,联合稀疏性比树稀疏性更重要。考虑到这些聚合示例中的树稀疏性,事实证明,所提出的多频CS模型的性能仅略好,但需要比传统模型高得多的计算复杂度。为了在重建质量和计算成本之间取得良好的平衡,所提出的多频CS模型选择β=0来增强联合稀疏性对这些聚集体示例的重要性。
第五节.结论
本文评估了一种新的多频CS模型,用于二维近场微波和毫米波SAR图像重建。除了标准稀疏性之外,这个新的CS模型还同时利用了多频测量中的联合稀疏性和每个频率测量中的树稀疏性。基于所开发的多频CS模型,结合分裂Bregman更新和并行FISTA类近端算法的变体,提出了一种CS方法,以最小化对应于最小二乘数据拟合的五个项的线性组合,多-ℓ2范数,多电视范数,联合稀疏性范ℓ1数, 和树稀疏性重叠 ℓ21 范数。仿真和实验测量的重建图像被测试用于测试所提出的CS方法的性能,结果表明,该多频CS模型对于处理二维近场多频SAR图像重建问题非常有效。
-
大师拉扎维关于毫米波电路的总结2011-08-29 2303
-
毫米波雷达方案对比2018-08-04 12207
-
毫米波技术的发展进程2019-07-03 2933
-
毫米波雷达是什么?2019-08-02 4492
-
毫米波雷达(一)2019-12-16 14661
-
毫米波应用的应用,四路毫米波空间功率合成技术介绍2020-11-05 3538
-
位到毫米波无线电介绍2021-02-19 2479
-
怎么采用PMAC多轴运动控制器设计毫米波多通道扫频远场测量系统?2021-04-09 1899
-
请问怎样去设计一种非线性微波毫米波电路?2021-06-22 2378
-
毫米波雷达的特点是什么2021-07-30 7173
-
毫米波技术基础2022-07-29 2547
-
了解毫米波 -- 之一2023-05-05 1395
-
序列SAR内波图像二维成像仿真研究2009-12-19 1079
-
图像的二维提升小波变换的FPGA实现2011-06-29 3878
-
浅谈微波毫米波射频芯片及技术应用优势2023-03-09 5342
全部0条评论

快来发表一下你的评论吧 !

