理解运算放大器的失真度和开环增益

在使用运算放大器进行电路设计的时候，往往会遇到一个问题，放大之后的波形总是跟理论预期的有差距。这个简答的运算放大器的问题，涉及到非常多的复杂概念，包括增益误差，失真度、负反馈、总谐波失真、非线性、开环增益，本文用比较简洁的语言深入解析下这个疑问。

理解失真度!

在一个跟随器电路中(如下图)，输入一个正弦波Vi，对于输出波形Vo是一个跟随Vi的正弦波，对于Vo和Vi波形从时域上来看，两者的差异程度即是失真度。但从实际应用的角度，很难去从时域的角度去衡量Vo和Vi两者的差异程度，所以在频域上，定义了一种描述正弦信号失真度的参数，称为总谐波失真(Total Harmonic Distortion, THD)。

总谐波失真(Total Harmonic Distortion)

 

 

对时域信号进行傅里叶变换，用如下公式表示THD，其中U1是基波的有效值;得到各次谐波大小，U2表示二次谐波，U3表示三次谐波, …Un表示n次谐波有效值，用UH表示所有谐波的有效值。

 

 

失真度用%表示，比如信号发生器发出的正弦波，其THD=0.01%，此外，也可以用dB来表示，THD=20log(THD)dB，对于THD=0.01%的正弦波，其失真度-80dB。

开环增益导致的放大倍数的误差!

 

 

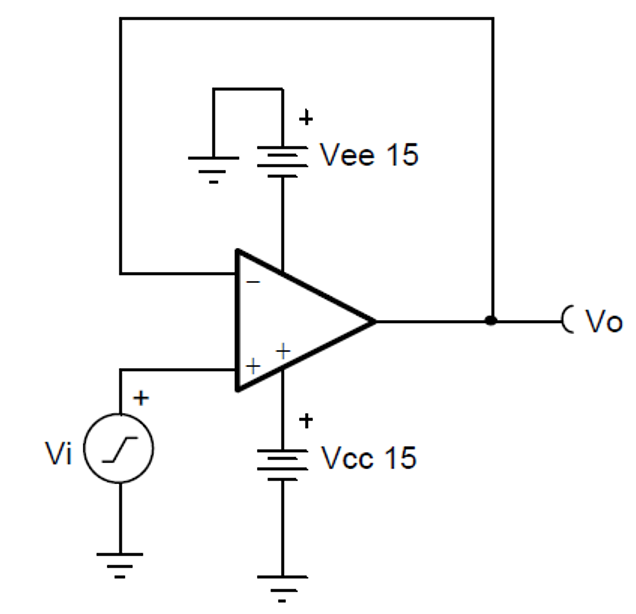
如上图，是一个同相比例放大电路(Close Loop Gain=2)，根据运算放大器开环增益的定义，Avol=Vout/(Vpos-Vneg)，可以得到：

 

 

同时，根据反相端的偏置电流为0，则Vneg的电压等于Vout在R1和Rf上的分压产生即：

 

 

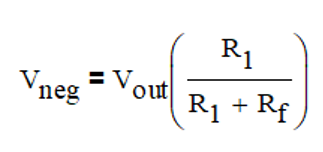
基于上述两个等式，整理可以得到闭环增益的表达式(如下)，从该表达式可以看到，实际对于同相比例放大电路，其闭环增益会受到开环增益的影响，只有当开环增益无穷大的时候，闭环增益才完全由比例电阻决定，Close Loop Gain=1+Rf/R1。

 

 

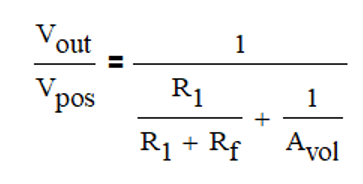
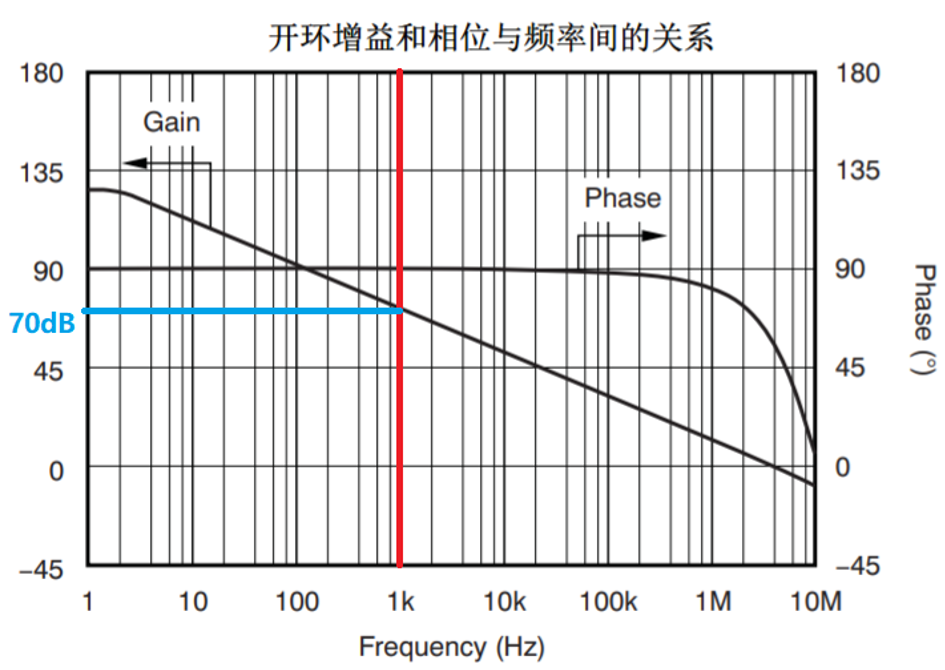
基于此，我们来看看对于实际的运算放大器，开环增益对1kHz的正弦波的放大的影响，下图是德州仪器OPA2171规格书中开环增益曲线，从图中读出在1kHz的时候，开环增益是70dB，即10^3.5=3162，将3162代入上述闭环增益表达式得到闭环增益是1.9987，相比预期的Close Loop Gain=2偏差了0.065%。

 

 

开环增益不是恒定的!

从上述分析，可以看到，如果对于1kHz的标准正弦波下，开环增益是固定的话，其只会带来闭环增益误差，这并不会带来非线性，即对于1kHz的正弦波放大2倍还是1.9987倍，其不会带来额外的次谐波，这样THD=0。

但实际上对于运算放大器其开环增益并不是恒定的，运放内部的是由多级晶体管构成，而晶体管的输入伏安特性曲线是指数型的，这就造成运算放大器的输入输出特性曲线是非线性的， 这就使得不同的供电、不同的共模输入均会导致实际开环增益的变化(通常运算放大器的规格书中标注的开环增益值都是在给定的条件下实测的值)，一旦对于1kHz的标准正弦波，在做2倍放大的时候，因为输入共模电压的变化，而导致开环增益一直处于变化中，这就导致放大后的正弦波是存在一定的失真。

但再回到上述对于闭环增益的公式(如下)，同样对于70dB@1kHz的开环增益，假如其开环增益变化范围从3000~4000变化，则闭环增益在1.9987~1.999这个区间变化，其闭环增益变化0.015%，实际对1kHz的正弦波的失真度影响非常小，如果我们进一步降低失真度，则可以选择同等条件下开环增益更大的器件。

 

 

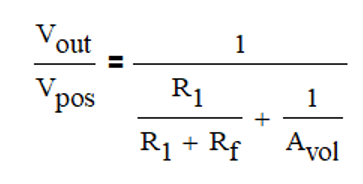
总的来说，如果想要获得更理想的放大倍数的输出波形，想要失真度最小的输出波形，可以选择同等条件下开环增益更大的器件。