深度学习基础知识(3)

2、多维数组的计算

多维数组：np.dim()可以获得数组的维数，np.shape()可以获得数组的形状，返回一个元组，对应每一个维度的元素个数。二维数组即矩阵。

矩阵乘法：np.dot(A,B)可以求A，B矩阵的乘积（点积），A(m×n)·B(n×k)=C(m×k)

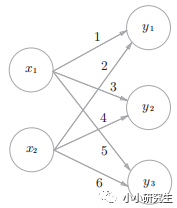
神经网络的内积：下图所示的简单神经网络，输入X是一维数组，W是二维数组，Y是一维数组。X(2)·W(2×3)=Y(3)
 

3、三层神经网络的实现
 

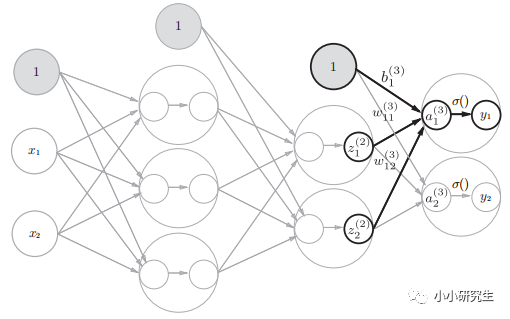
前向传递：输入到输出的传递。需要注意的是目前代码中的W，B都是人为赋值的。

1'从输入到第一个隐藏层：

A(1)=XW(1)+B(1)其中A(1)是输入层中的具有两个元素的一维数组，W是(2,3)的二维数组，B是具有三个元素的一维数组。用一行代码即可实现：

A1=np.dot(X,W1)+B1

激活函数选择sigmoid()，第一个隐藏层中神经元是激活函数转换后的输出:

Z1=sigmoid(A1)

2'从第一个隐藏层到第二个隐藏层：

第一个隐藏层的输出Z1第二个隐藏层的输入X：A2=np.dot(Z1,W2)+B2

Z2=sigmoid(A2)

3'第二个隐藏层到输出层:

A3=np.dot(Z2,W3)+B3

激活函数选用恒等函数y=x，需要自己定义：

def identity_function(x):

    return x

Y=identity_function(A3)

4、输出层的设计

输出层激活函数，一般回归问题可以用恒等函数，二元分类问题用sigmoid函数，多元分类问题用softmax函数。分类是区别输入属于哪一个类别的问题，回归是预测一个数值的问题。

已经介绍过恒等和sigoid，现在介绍一下softmax函数。

yk=exp(ak)/∑1nexp(ai)

输出层有n个神经元，第k个输出是第k个输入的指数函数除以每个输入的指数函数的和，输出与所有输入都有关。这个函数需要定义才能使用，注意这个函数用到指数函数，存在溢出的问题，需要对分子分母同除以一个常数，即分子分母的指数同减去一个常数，为了防止溢出，取输入的最大值：

def softmax(a):

    C=np.max(a)

    exp_a=np.exp(a-C)

    sum_exp_a=np.sum(exp_a)

    y=exp_a/sum_exp_a

    return y

softmax函数的特征是输出0-1之间的实数，且输出值的总和为1，因此可以把函数的输出解释为概率。输出层神经元的数量就是类别的数量。由于指数函数单调递增，输出最大值的即概率最高的分类。一般神经网络只把输出值最大的神经元对应的类别作为识别结果。