说一说IQ调制和星座图

IQ信号是什么

先说说IQ数据是用来干什么的。在通信系统中，通信所用的电磁波最基本的参数是频带和带宽，这两个参数不做介绍，对通信有了解的人应该都不会陌生。电磁波的频率不会从0开始，电磁波所处的频带的中心频点被称作中频，减掉中频之后的信号被称作基带信号。真正承载有用的信息的是基带信号。举例说明：假设广播电台的频段是800.9MHz~900.1MHz，那么其带宽是200kHz，中频是900MHz，减掉中频之后[-100kHz, 100kHz]的信号被称作基带信号。所以在接收到信号之后直接减掉中频的RF接收机就叫零中频接收机。

在通信的过程中不可能直接传输基带信号，要把基带信号放在中频上才能进行传输，因此中频也叫做载波。当我们需要传输数据时，首先要把基带信号放到载波上，就像我们要运货物的时候要先把货搬到车上，这个过程叫做上变频，到达目的地之后要卸货，这个过程叫下变频。假设基带信号为cos(a)，载波为cos(b)，上变频所期望的结果就是cos(a+b)，令a+b=c，则下变频期望的结果就是cos(c-b)。上变频与下变频的过程统称为混频。那么混频是怎么实现的呢？其实从数学上也比较好理解，三角函数要实现频率的变换，就得通过乘法来实现。两个不同频率的信号相乘得到的结果请看下面的式子

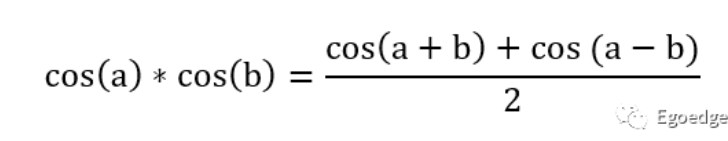
其实这个结果在模拟锁相环那一篇里面有过介绍。混频的过程总是伴随着频率差和频率和两个结果，这也是频率镜像的来源。和模拟锁相环的环路滤波器目的正好相反，我们需要在这个结果中滤掉频率差保留频率和。为了得到单一的和或差的信号，于是将差的部分展开，得到如下结果：

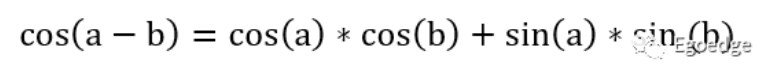
上式中sin(a)和sin(b)则是和cos(a)、cos(b)相差90°的信号，也就是正交的IQ信号。这个式子很清楚的表明IQ信号在混频过程中所带来的便利。对于基带的数字信号来讲，有IQ信号之后就可以很方便的进行上下变频的操作。

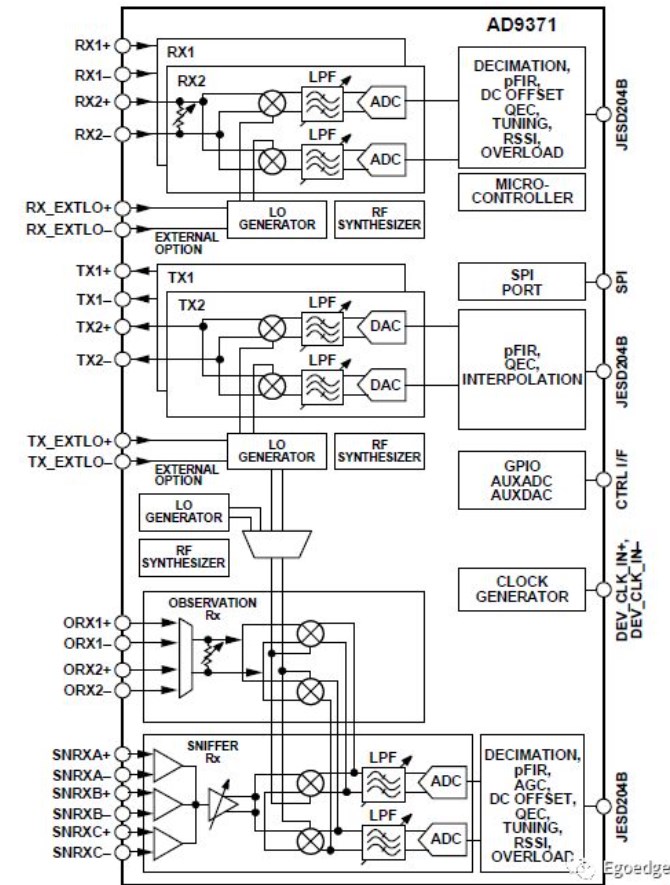
这是一个典型的捷变频收发器的框图，其内部集成了本振，也可以选择外部输入本振信号，直接进行上下变频之后进行采集和播放的步骤。
 

IQ调制

利用IQ信号对数据进行调制的方式就是IQ调制，IQ调制被广泛的运用在通信信号的编码中。关于IQ调制的理解还是倒着说边角容易理解。IQ调制的过程见下图。

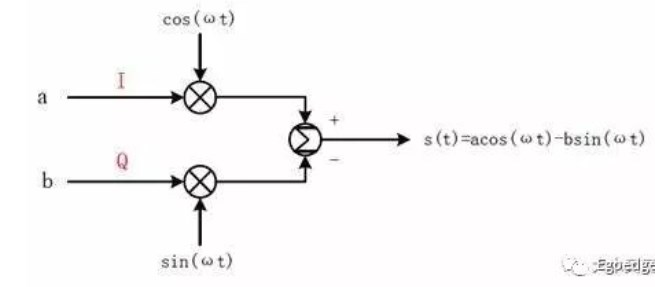
输入的ab两路信号分别乘以cos(ωt)和sin(ωt)，之后再相加（通常sin函数的符号为负）就得到了IQ调制之后的信号。而对应于a/b不同的取值，θ有不同的取值。

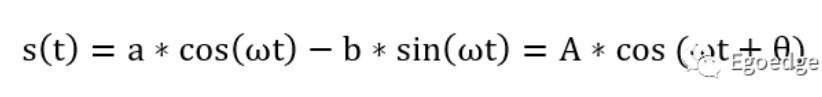
那么被称为I/Q数据的a路和b路数据时从哪里来的呢？我们的数据是一连串连续的bit，而a/b两路数据就是和这些bit直接做映射得到的结果。一次对每两个bit做编码时，只需要给a和b定义两个值即可，对4个bit做编码时需要给a和b定义4个值，以此类推。

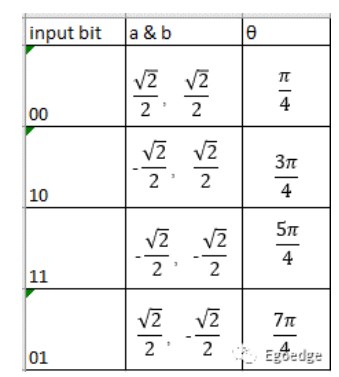
上表中a和b的取值是为了使输出幅度为1，当一次对4个bit做编码时，其映射关系见下表。

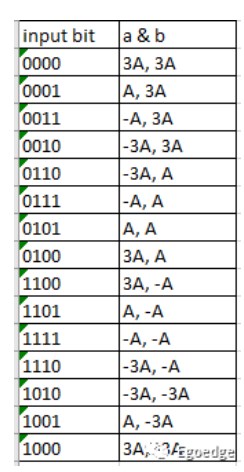
那对于编码映射的过程是可以随意定义的吗？显然不是，为了使IQ调制之后输出的相位误差最小，相邻的相位之间只有1个bit的差别，也就是格雷码。

星座图
 

通信系统中经常见到星座图这个概念，什么是星座图，又是用来干什么的？

在通信技术的发展中，1G时代是模拟通信，从2G时代开始就进入了数字通信技术的时代，现在1G已经几乎被完全淘汰。在通信制式中，有调幅、调频和调相3种形式。

在模拟通信中，在指定的频段中，调频波是连续的，类似于雷达波中常用的chirp信号。雷达中用chirp信号是为了方便做脉冲压缩，使多普勒频移更加明显进而提高速度分辨率，但在通信系统中，多普勒频移则是我们所不期望的。

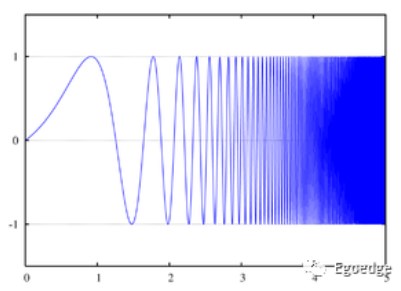
到了数字通信的时代，在调频中的频率则是不连续的。在频段中，用不同的频点来分别表示0和1。下图清楚的表示出了调幅调频和调相的具体调制方式。

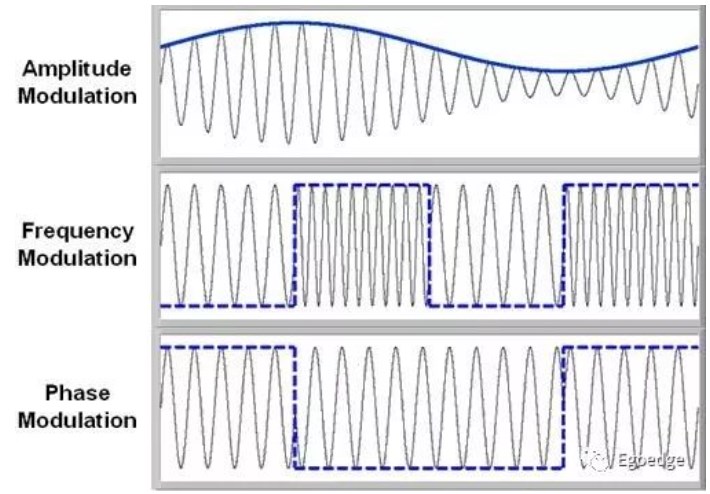
PSK，相移键控，顾名思义，是通过按键来控制信号输出相位的改变。通过输入0/1信号来控制相位的改变是一种很容易实现的调制方式。把PSK和上面的IQ调制结合起来就可以方便的完成调制过程。当一次对2bit做编码时，共有4种相位，对应IQ的4种不同组合，这种调制称为QPSK；对4bit做编码时共有16种相位，称为16PSK。

我们把输入的IQ信号定义为信号的实部和虚部（但实际上IQ两路信号都是实信号）将I和Q分别作为横轴和纵轴，那么在复平面上每两个IQ值可以对应一个固定的点，将坐标图画出来就叫做星座图。

PSK和QAM二者本质的区别在于PSK的点分布在一个单位圆上，而QAM的点并不分布在单位圆上，这意味着输出信号的幅度并不是一定的，所以QAM的编码方式对于频谱的利用率是PSK编码的几倍。

格雷码的编码方式保证了1bit的误码只会让星座图上的点在相邻的点之间跳变，不同的编码方式和映射关系对于五码性能也是有影响的，这就属于统计学的领域了，不做讨论。

在QAM的星座图上，相对于原点的距离也就是信号的功率，信号的功率会直接反映在星座图上。