深度学习基础知识(5)

上一节中说到，需要求使损失函数最小的权重和偏置，高中数学中，求函数的极值就是使函数导数为0的点。

1、导数

导数是某个瞬间的变化量，瞬间的定义是时间趋近于0

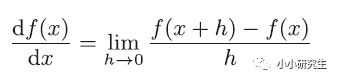
使用代码来实现：

def numerical_diff(f,x):
  h=10e-50
  return(f(x+h)-f(x))/h

此时，h取一个极小的数来表示趋近于0，但是如果太小的话在计算机中贵产生舍入误差，用float32的浮点数来表示依然是0.0。另外，上述定义是函数f在x与x+h之间的差分，是近似的导数定义，而真正的导数是曲线在某一点上的切线，这个误差产生是由于h不可能无限趋近于0。因此，可以计算f在x+h和x-h之间的差分进一步减小误差。

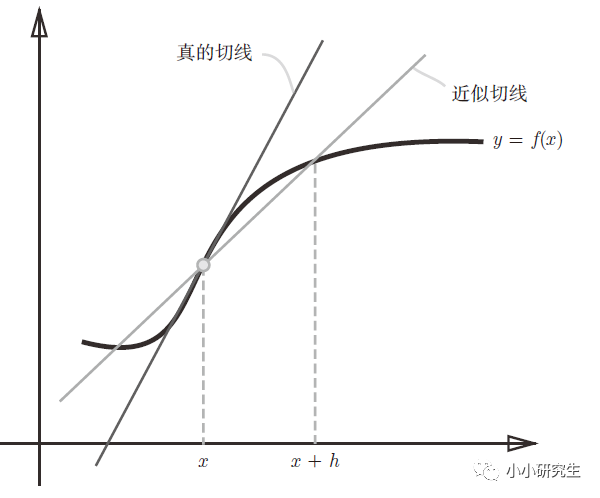
真正数值微分的代码：

def numerical_diff(f,x):
  h=1e-4
  return (f(x+h)-f(x-h))/(2*h)

真正用函数的导数计算出的结果是解析解，而数值微分近似的结果严格意义上并不一致，但是由于误差可以忽略不计，因此可以认为它们是相等的。

2、偏导数

当函数y有多变量时，多变量函数的导数就是偏导数。求偏导数时，多变量中的一个变量是目标变量，其他变量需要为定值。

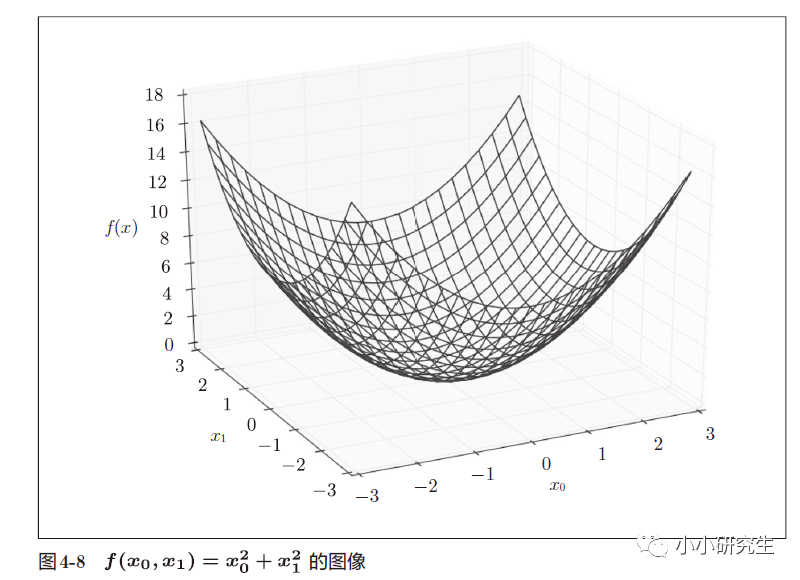
求偏导的代码：

def function_2(x):
  return x[0]**2+x[1]**2

3、梯度

偏导数汇总而成的向量成为梯度。

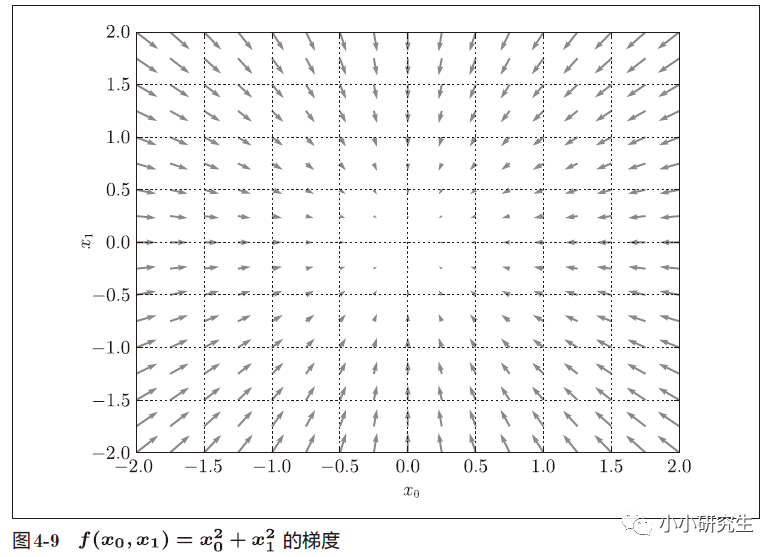
向量是有大小和方向的，在梯度图中，箭头的指向就是梯度的方向，箭头的长度就是梯度的大小。 梯度总是指向函数值减小最多的方向。

知道梯度的定义，就可以用梯度来使损失函数减小。复杂函数中，梯度指示的方向基本上都不是函数值最小处，但沿着梯度方向可以最大限度减小函数的值。在梯度法中，函数的值从当前位置沿着梯度方向前进，然后在新的地方重新求梯度，再沿着新梯度的方向前进，不断重复，逐渐减小函数值。寻找最小值的梯度法是梯度下降法，寻找最大值的梯度法是梯度上升法，一般神经网络中梯度法主要是指梯度下降法。

4、梯度法求某个函数值优化结果

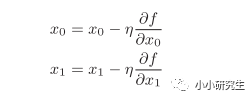
η是学习率，表示更新量，决定在一次学习中，应该学习多少以及在多大程度上更新参数。上式会反复执行，逐渐减小函数值。学习率需要事先确定，过大或过小都不行，一般会一边改变学习率一边确定学习是否正确进行。

梯度下降法代码：

def gradient_descent(f,init_x,lr=0.01,step_num=100);
  x=init_x
  for i in range(step_num):
    grad=numerical_gradient(f,x)
    x-=lr*grad
    return x

参数f是要最优化的函数，init_x是初始值，lr是学习率，step_num是重复次数。 numerical_gradient()会求函数梯度，并更新x。

当使用梯度法求f(x0,x1)=x0^2+x1^2的最小值时，设置初始值为(-3,-4)，学习率为1，上面次数定义的时候是100，实际使用的时候设置是20，最终结果为[-0.03458765 0.04611686]。 使用解析法求最小值是[0,0]，因此结果在一定程度上可以认为是一致的。

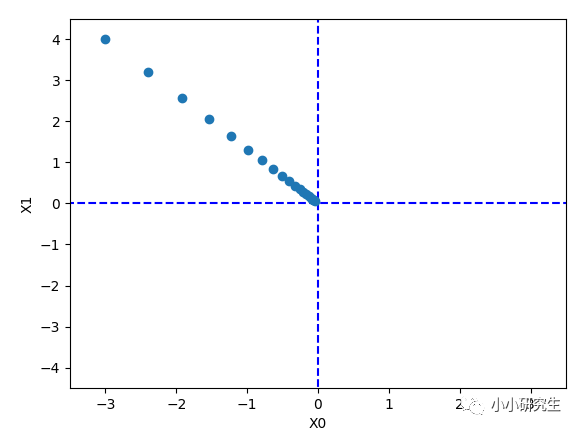
对梯度法每次迭代进行绘图显示，函数的取值在向原点(最小值处)逐步靠近。

学习率的设置非常重要，当我们将其设置为10时，结果为[-2.58983747e+13 ，-1.29524862e+12]发散成一个很大的值。 当设置成1e-10时，结果为[-2.99999999 ， 3.99999998]几乎没有什么变化。 学习率这种超参数和权重偏置不同，只能人工设定，需要尝试多个值。

5、梯度法求神经网络的损失函数优化结果

class simpleNet:
    def __init__(self):
        self.W = np.random.randn(2,3)
    def predict(self, x):
        return np.dot(x, self.W)
    def loss(self, x, t):
        z = self.predict(x)
        y = softmax(z)
        loss = cross_entropy_error(y, t)
        return loss
x = np.array([0.6, 0.9])
t = np.array([0, 0, 1])
net = simpleNet()
f = lambda w: net.loss(x, t)
dW = numerical_gradient(f, net.W)
print(dW)

init (self)创建一个随机的2*3的矩阵，predict(self,x)让x与W矩阵相乘，loss(self,x,t)定义了损失函数。 给定了x,t之后调用了实例化的类，再将net.loss传递给f后，在numerical_gradient()函数中进行调用求梯度。

至此，求出了神经网络的梯度，接下来只需要根据梯度法更新权重参数。