频域中的奈奎斯特-香农定理

在上一篇介绍奈奎斯特-香农定理的文章中，我们看到当以每个周期不提供至少两个样本的频率对波形进行采样时，正弦波的频率特性将无法挽回地丢失。换句话说，如果我们以低于奈奎斯特速率的频率进行采样，我们就无法完美地重建正弦曲线。

然而，大多数信号不是单频正弦波。例如，调制的 RF 信号具有与载波和基带波形相关联的频率，代表人类语音的音频信号将覆盖一定范围的频率。 

我们使用傅立叶变换来可视化信号的频率内容。时域图是传达单频信号背景下采样率不足的影响的好方法，但对于其他类型的信号，我宁愿使用频域。

采样的频域效应

假设我们想要数字化一个音频信号，该信号包括指定范围内的许多不同频率的混合。范围的高端定义为 f MAX，我们假设范围向下延伸至 DC，即使我们听不到那么低的频率。这种信号的傅里叶变换可能看起来像这样：

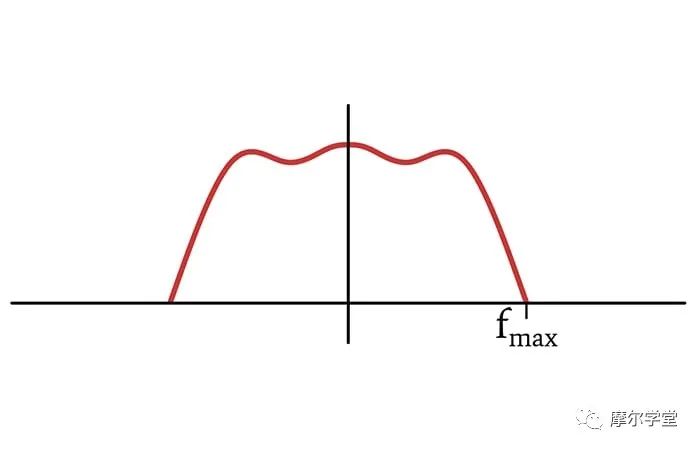
时域中的数学采样

在数学领域，理想采样等效于将原始时域波形乘以一系列 delta 函数，间隔等于 1/f SAMPLE，我们称之为 T SAMPLE。（对于本文的其余部分，我们将使用 f S表示 f SAMPLE并使用 T S表示 T SAMPLE。）这种乘法导致采样信号在 delta 函数之间为零，并在每个点保留原始信号的值在与 delta 函数重合的时间。

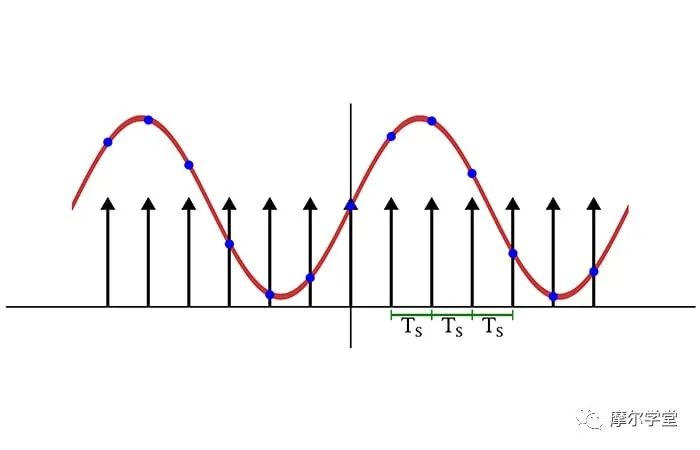
以数学方式实现的时域采样：我们将模拟信号乘以以采样频率出现的一系列 delta 函数。

频域中的数学采样

这种时域采样过程如何影响信号的频域表示？让我们来看看。

首先要记住的是，时域中的乘法变成了频域中的卷积。因此，我们可以通过将原始信号的傅里叶变换与delta函数的傅里叶变换进行卷积来求出采样信号的傅里叶变换。

事实证明，delta-function train 的 Fourier 变换是 delta-function train。不同之处在于 delta 函数由对应于采样频率而不是采样周期的水平距离分隔。

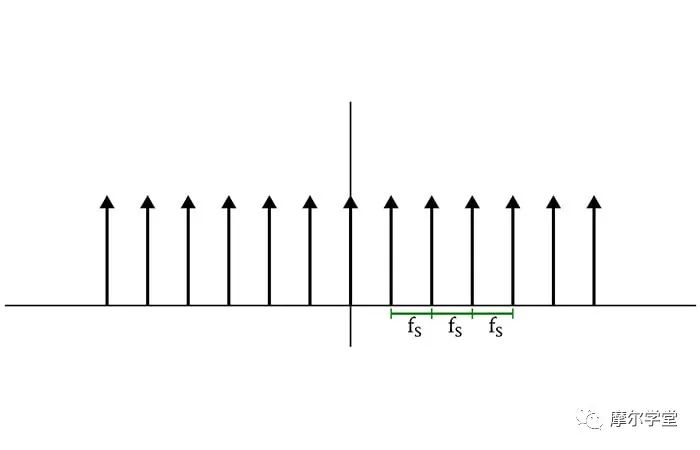
由采样周期分隔的一系列 delta 函数的频谱是由采样频率分隔的一系列 delta 函数。 

当我们将 delta 函数的频谱与原始信号的频谱进行卷积时，我们创建了根据 delta 函数的位置移动的原始频谱的副本。因此，采样信号的频谱由多个相同的“子频谱”组成，这些“子频谱”以±f S、±2f S、±3f S等为中心。

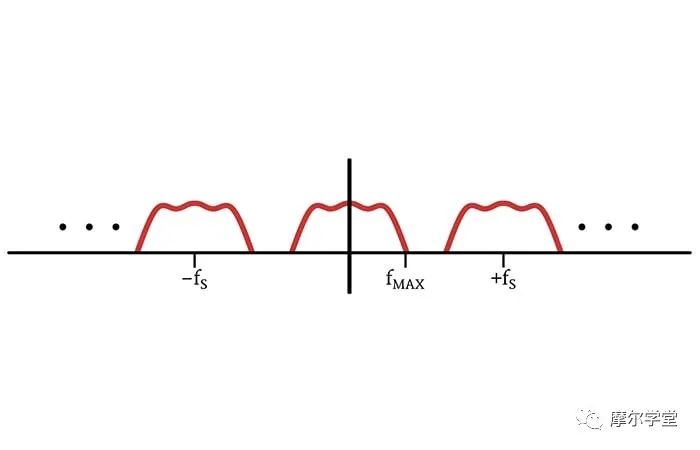
足够的采样频率会导致子光谱发生足够的偏移以保持完全分离。 

我们现在拥有通过频域分析确认奈奎斯特-香农定理所需的信息。正如我在上一篇文章中表达的那样，这个定理如下：

如果系统以超过信号最高频率至少两倍的速率对模拟信号进行均匀采样，则可以从采样产生的离散值中完美地恢复原始模拟信号。

由于傅立叶变换的负频率部分，原始信号的完整数学带宽为 2f MAX。因此，为了确保子光谱不重叠，我们必须将它们至少移动 2f MAX。换句话说，采样频率必须比信号的最大频率至少高两倍。

如果满足这个条件，就可以完美地重建原始信号。为什么？因为原始光谱没有改变，我们可以通过低通滤波去除其他子光谱。（下一篇文章将更详细地探讨这一点。）如果不满足条件，则子频谱重叠，原始频谱被改变，再多的低通滤波也无法恢复原始信号。

混叠

当我们使用低于奈奎斯特速率的采样频率时，子谱重叠是信息被破坏的原因。子谱的重叠部分通过加法合并；如果我们尝试使用低通滤波器分离出原始频谱，重叠频带中的频率成分将不同，因此相应的时域信号将不同。

这个的正式名称是aliasing。

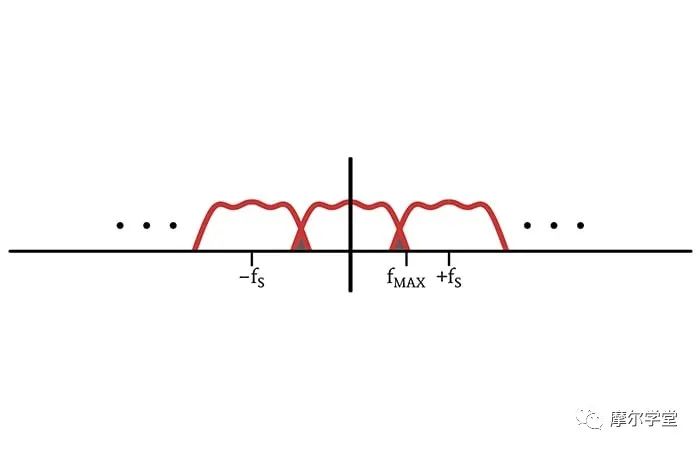
棕色阴影的三角形区域表示导致光谱改变的混叠。 

名词“别名”的定义之一是“虚假或假定的身份”。我们使用术语“混叠”是因为这种采样现象会导致一个频率分量移动到频谱中的一个新位置，从而将其自身“伪装”为不同的频率。

我们在上一篇文章中看到了这一点，其中以 1.1f信号采样导致离散时间波形的频率似乎远低于原始模拟波形的频率。

结论

至此，我认为我们已经涵盖了抽样理论的基础方面。在下一篇文章中，我们将开始在理论和实践之间建立一些联系。

彩蛋来了

5月30-31号、6月08-09号，两期从基础到高级的ADC讲座，将涵盖高速ADC设计的原理、传统架构和最先进的设计。第一部分首先回顾了ADC的基本知识，包括采样、开关电容和量化理论。接下来，介绍了经典ADC架构的基础和设计实例，如闪存、SAR和流水线ADC。然后，本教程将对混合型ADC架构进行总体概述，这就结束了第一部分。在第二部分，首先描述了ADC的度量。然后，介绍混合或非混合架构的各种先进设计。该教程最后将以数字辅助解决技术结束。

　　审核编辑：汤梓红