

温习一下运算放大器的基础知识
电子说
描述
运算放大器: 我们也称之为运放,根本上说是一种电压放大设备。在运放的输入和输出端子之间添加外部反馈元件,例如电阻和电容,这些反馈元器件决定了运放的最终功能。
我觉得这句话说的特别好,一句话道破了运放的本质,其实就是一个放大器加各种RC组合,其实一种方法是你可以把RC和运放的﹢和﹣各种组合做个表格,其实也就产生了 各种运算放大器 。
大多数的运放都是电压放大器,所以我们也只考虑电压放大的运放。
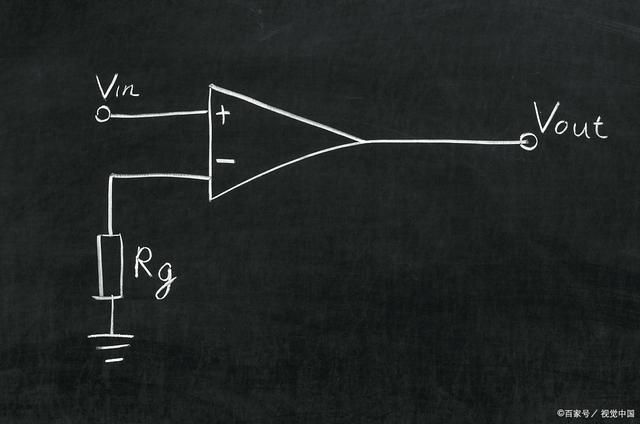
理想运算放大器的等效电路

图片来自electronics-tutorials
运算放大器的理想化特性:
开环增益Avo
无限 ——运算放大器的主要功能是放大输入信号,开环增益越大越好。开环增益是没有正反馈或负反馈的运算放大器的增益,对于这样的放大器,增益将是无限的,但典型的实际值范围从大约 20,000 到 200,000。
输入阻抗Zin
无限大 ——输入阻抗是输入电压与输入电流的比值,假设为无限大,以防止任何电流从源电源流入放大器输入电路 ( I IN = 0 )。真正的运算放大器具有从几皮安到几毫安的输入漏电流。
输出阻抗Zout
零 ——假设理想运算放大器的输出阻抗为零,作为一个完美的内部电压源,没有内阻,因此它可以为负载提供尽可能多的电流。该内部电阻实际上与负载串联,从而降低负载可用的输出电压。实际运算放大器的输出阻抗在 100-20kΩ 范围内。
带宽 BW
无限 ——理想的运算放大器具有无限的频率响应,可以放大从直流到最高交流频率的任何频率信号,因此假定它具有无限带宽。对于真正的运算放大器,带宽受增益带宽积 (GB) 的限制,它等于放大器增益变为单位时的频率。
失调电压Vio
零 ——当反相输入和非反相输入之间的电压差为零、相同或两个输入都接地时,放大器输出将为零。实际运算放大器具有一定量的输出失调电压。
从上面的这些“理想化”特性,我们可以看出输入电阻是无穷大,因此 没有电流流入任一输入端 (我们理解为 虚断 ,正负端到运放内部的电路,相当于完全断开”), 差分输入失调电压为零 (“输入的正负两端,如果工作起来之后,正负端相当于短路,也就是电压接近于相等,这是 虚短 ”)。记住这两个属性很重要,因为它们将帮助我们了解运算放大器在运算放大器电路的分析和设计方面的工作原理。
开环频率响应

这个图给了我们很多信息,首先在低频时,开环增益可以达到100db,(不知道db的意思自行查阅,这里其实对于输出比输入相当于放大了10万倍),从上图斜率恒定的这一段可以看出来增益与频率的乘积在曲线上的任何点都是恒定的。这里就引入一个新的概念,叫增益带宽积 GBP。
例如,根据上图,放大器在 100kHz 时的增益为 20dB 或 10,则增益带宽积计算为:
GBP = A x BW = 10 x 100,000Hz = 1,000,000。
再随便找一个点:
GBP = A x BW = 1,000 x 1,000Hz = 1,000,000。
运算放大器的电压 增益 (AV) 可以使用以下公式找到:
Voltage Gain=Vout/Vin
以分贝为单位:
20log(Voltage Gain)得到的数值就是以dB为单位的增益。
运算放大器带宽
运算放大器带宽是放大器电压增益高于其最大输出值的 70.7% 或 -3dB (其中 0dB 为最大值)的频率范围,如下所示。
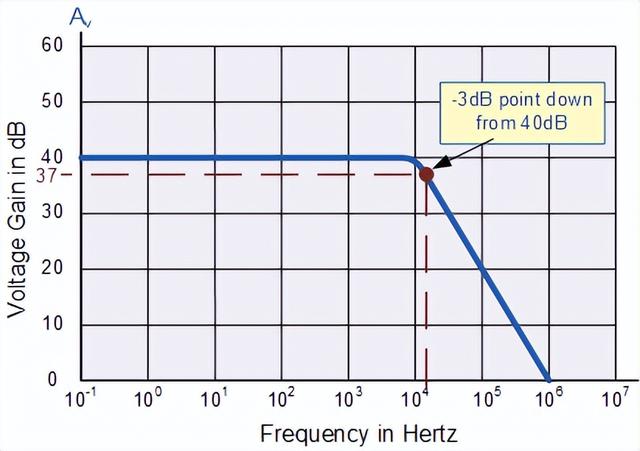
这里我们以 40dB 线为例。频率响应曲线的 -3dB 或 Vmax 下降点的 70.7% 给出为 37dB 。取一条线直到它与主要 GBP 曲线相交,这给我们提供了一个频率点,正好在 10kHz 线上方,大约 12 到 15kHz。
实例1:
已知放大器的增益带宽积GBP是1000000,又已知37db是带宽对应的增益,求该放大器的带宽。
那么首先我们可以计算出37db对应的增益为:37 = 20 log (A),求得A=70.8
GBP÷A=带宽,则有1000000÷70.8=14.124Khz.
那么得到该频率就是该放大器的 带宽 。
-
运算放大器基础知识分享2019-07-21 0
-
【运算基础教学篇】运算放大器基础知识2021-02-20 0
-
运算放大器应用基础2008-04-23 2039
-
运算放大器的应用2008-04-23 529
-
运算放大器,运算放大器是什么意思2010-03-09 3814
-
集成电路运算放大器与理想集成运算放大器2017-01-16 9835
-
一文看懂运算放大器的前世今生2020-05-28 6494
-
实用运算放大器的基础知识及其应用的简介2021-05-04 3077
-
运算放大器的应用及种类介绍2021-10-02 8264
-
小编科普一下运算放大器的基本电路2022-07-13 50947
-
运算放大器的基础知识2022-08-01 8480
-
集成运算放大器基础知识2022-10-20 505
-
反向运算放大器讲解2023-05-18 2928
-
运算放大器和比较器的基础知识2024-07-13 328
全部0条评论

快来发表一下你的评论吧 !

