太赫兹频段粗糙表面散射特性研究

摘  要

当电磁波频率增大到太赫兹频段时，太赫兹波的波长与粗糙表面微结构可比拟。粗糙表面将对太赫兹波的传播机理产生重要影响，散射在传播中将发挥关键作用。当下针对太赫兹频段散射特性的研究主要依靠大规模测量，较难实现。因此，使用建模的方法生成符合实际物理分布的粗糙表面，借助全波仿真的方法研究太赫兹波和表面粗糙度的作用机理是研究太赫兹波散射特性的新途径。提出使用轮廓仪捕获典型材料的物理分布特性，并从中提取粗糙面的关键统计参数。基于蒙特卡罗方法，依据统计参数重建该表面的物理分布。将测量表面和重建表面导入Feko进行全波仿真，比较并验证该研究方案的可行性。

0 1   

概  述

当下，无线通信系统面临着2个关键问题：传统频谱资源的日益短缺和无线网络需求的飞速增长，这迫使无线通信行业亟需开发新的频谱资源以满足用户的迫切需求。在无线通信领域，有限的频谱极其珍贵，对通信、广播、信息网络等领域极其重要［1］。而随着无线通信行业的发展，较低频段的频谱资源已不能满足人们对无线网络的需求，使得无线通信行业开发更高频段的频谱资源以满足市场的需求。

太赫兹（Terahertz，THz）频段是介于毫米波和红外波之间，频率在0.1~10THz，它在电子学领域被称为亚毫米波，光谱学领域被称为远红外射线，是目前通信研究的热点频段。太赫兹波是目前电磁波谱中唯一一个没有获得全面研究且充分利用的波谱“空白”区［2］。在未来的通信中，太赫兹频段的无线通信有着高数据率的潜力，有望分担繁重的通信压力［3］。因此，对该波段的研究是通信行业当前和未来的重点研究方向之一。对于太赫兹通信而言，由于其波长与环境中大部分表面的粗糙度可比拟，太赫兹波的传播机理将发生重要变化，散射将成为关键的传播机理。

当前针对太赫兹频段散射特性的研究主要依赖于昂贵的太赫兹测量设备和大规模的材料测量。但是，由于太赫兹频段恰好处于由宏观电子学向微观光子学过渡的频段，目前目标材料对太赫兹波的响应机理尚且不明，目标表面可与波长比拟的细微结构对太赫兹波散射的影响规律也不清楚，同时有效的散射特性计算方法与实验测量手段缺乏，这些问题给太赫兹频段目标散射特性理解与太赫兹雷达技术的实际应用带来了严峻挑战。由于太赫兹的衍射和反射相比微波或者毫米波较弱，室内任何的障碍物和移动的人体都有可能破坏通信条件。太赫兹测量设备价格昂贵，实验环境较为严格，对于实际实验室测试的要求较高，实际研究成本较大，且结果易受环境影响［5］。对于太赫兹频段电磁波的研究，传统的实际测量研究方法不能满足大多数情况下的研究要求，过高的测试设备要求导致研究成本昂贵。因此，电磁计算仿真成为了优选的研究方法，对于精确仿真室内环境下的太赫兹通信系统的散射十分重要。

本文利用三维轮廓仪捕获实际粗糙面的高度分布特性，同时基于蒙特卡洛方法依照测得关键参数对粗糙表面进行随机建模，借助全波仿真工具Feko进行电磁仿真，得出由实际粗糙表面和建模重新生成的粗糙表面的散射特性。比较2个表面的散射电场分布，验证利用该方法研究粗糙面散射特性的可行性。

0 2   

表征粗糙表面分布的关键参数

研究粗糙面表面粗糙度对散射的影响首先需要确定粗糙面的统计参数，目前已经有相关理论对粗糙面高度分布的统计量进行介绍［6］。随机粗糙面的高度起伏均方根高度δ和表面相关长度l是描述粗糙表面高度分布特性的2个基本统计参数。

2.1  均方根高度 δ

以一维情况为例，设随机粗糙面的高度起伏为z=f（x），它的概率密度函数p（f）反映高度起伏的分布情况［7］。粗糙面的均方根高度δ反应粗糙面粗糙程度，定义为：

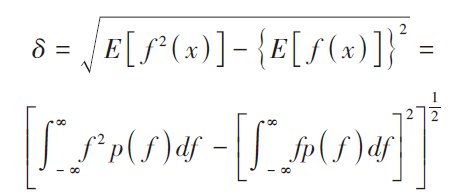
（1）

对于二维粗糙面同理，将积分域从X方向变换为XOY平面，计算得出均方根高度即可。

2.2  相关长度l

对于特定分布的粗糙表面，单一的均方根高度并不能唯一地描述粗糙面的特性，所以引入自相关函数表明随机表面上任意2点间的关联程度［8］，从而更准确地描述粗糙面特性，定义自相关函数为：

G(R)=E[f(x)f(x+R)]

（2）

δ2是粗糙面表面的高度方差，因此对自相关函数进行归一化，定义相关系数为：

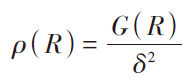
（3）

表面相关长度l是估计表面上任意2点是否相互独立的一种基准，即若表面上2点在水平距离上相隔距离大于l，则可认为这2点的高度值在统计学上近似相互独立。根据上述定义，将相关系数ρ(R)降为1/e时的R值称为相关长度l，即ρ(l)=1/e。对于二维粗糙面，单一方向的相关长度不能很好的描述其任意2点间的相关性，因此引入lx，ly 2个统计参数来分别描述其不同方向的相关性。

0 3   

基于蒙特卡洛法的粗糙表面建模

3.1  蒙特卡洛法

蒙特卡洛方法又称线性滤波法[9]，其基本思想是在频域用功率谱对其进行滤波，再对结果做逆快速傅里叶变换得到粗糙面的高度起伏。由于粗糙表面被认为由大量的谐波叠加而成［10］，谐波的振幅是独立的高斯随机变量，其方差正比于特定波数的功率谱密度S(k)。假设要产生的二维随机粗糙表面在X和Y方向上的长度分别为lx和ly，等间隔离散点数分别为M和N，相邻2点间的距离分别为Δx和Δy，则粗糙面上每一点的高度可表示为：

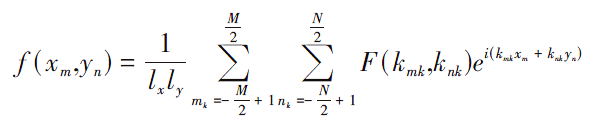
（4）

其中，

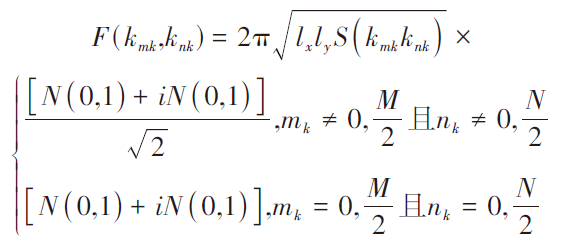
（5）

其中，离散波数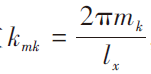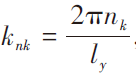，，N(0,1)表示均值为0，方差为1的正态分布随机数。S(kmkknk)为服从高斯分布的粗糙面的功率谱函数。

3.2  实际表面的高度分布

采用某三维扫描仪［11］（扫描精度高、数据量大，能在光学扫描过程中产生极高密度数据）捕获表面的三维物理分布，实现对材料的三维建模。对轮廓仪进行基本的校正，让其左右相机对焦于所测材料的平面，并调整好曝光度与清晰度。将标定板置于材料平面进行标定，将所测材料贴上标定点并置于平面上，这里以瓷砖为例，待测样本如图1（a）所示。从不同角度扫描瓷砖，然后对所得数据进行拼接，得到瓷砖的三维模型，导出为stl文件并处理［12］，扫描拼接后的结果如图1（b）所示。

图1 瓷砖实物与轮廓仪扫描结果对比

提取其分布参数，借助分布拟合工具拟合粗糙表面的高度分布特性（见图2）。从图2可以看出，瓷砖表面的高度服从均值为0.028mm、标准差为0.135mm的高斯分布。依据式（1），拟合的标准差即为表面的均方根高度。

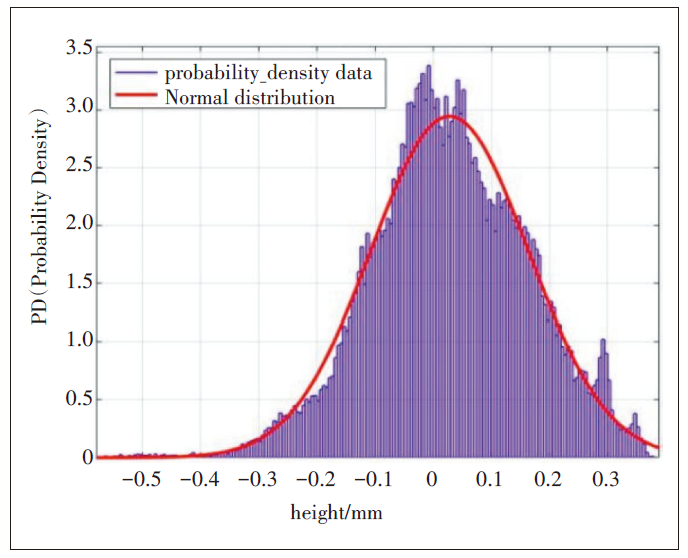
图2 瓷砖表面高度分布拟合

基于测量数据和式（2）~（3），计算得到表面在X与Y方向的相关系数ρ(R)，如图3所示。

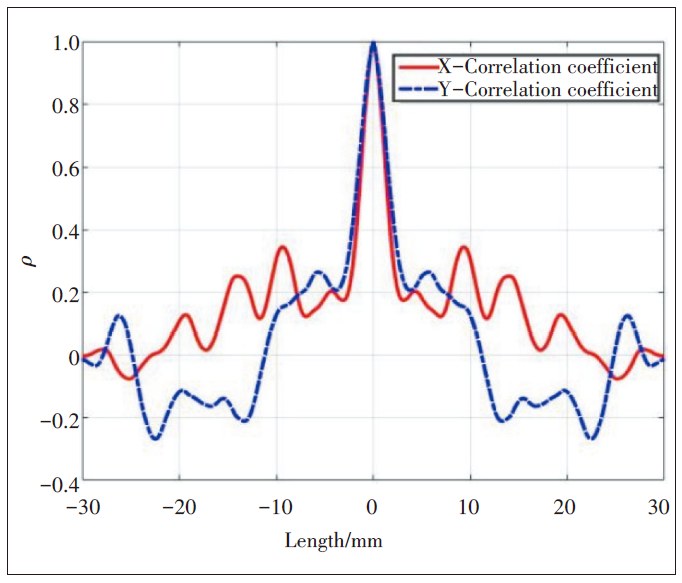
图3 瓷砖表面相关系数

将相关系数ρ(R)降为1/e时的R值称为相关长度l，即ρ(l)=1/e，记录X与Y方向的相关长度。计算得出2种材料的均方根高度与相关长度，如表1所示。

表1 材料的粗糙面统计参数

3.3  基于蒙特卡洛法生成随机粗糙面

依据式（4），通过蒙特卡洛方法[13]重建均方根高度为0.13533mm，相关长度分别为lx=1.80mm、ly=2.24mm的三维粗糙表面（见图4）。

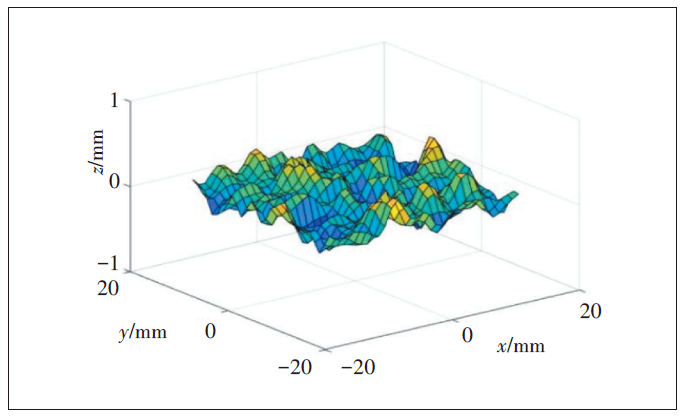
图4 重建的随机粗糙面

0 4   

粗糙表面散射特性

Feko是一款基于积分方程方法求解麦克斯韦方程组任意结构通用的三维电磁场仿真软件。Feko支持对外部导入的三维模型进行仿真，可以设置模型的材质、激励源频率和角度、求解算法等参数，还能在不同维度上对比仿真结果，能够很好地满足实验需求，其电磁计算结果的准确性得到了行业的认可。

4.1  仿真设置

瑞利判据常用来判断一个表面是否是粗糙的，瑞利判据公式如下：

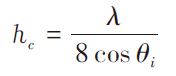
（6）

式中：

λ——波长

θi——入射角

h0——粗糙表面最大高度差，若h0大于hc，则认为表面是粗糙的，反之则可认为它是光滑的

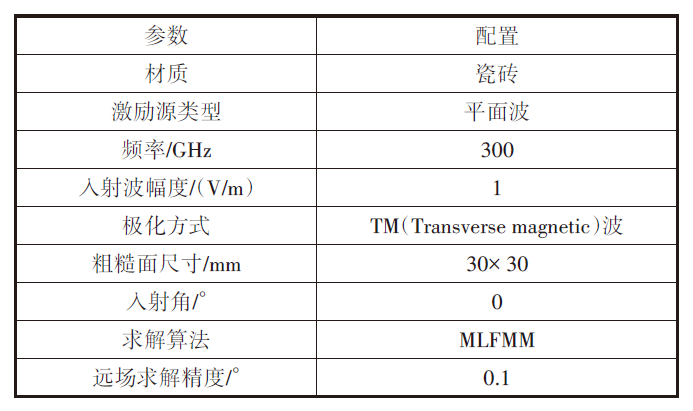
导入材料粗糙面，增加并选择所需的参数与材质，进行网格剖分，重新划分网格面，提升粗糙面的精度。然后采用多层快速多极子方法（Multi Level FastMultipole Method，MLFMM）［14］，基于分组思想，将规模为N的分组逐层计算单元间的相互作用，对内存的需求正比于N×log（N），极大节约了计算资源，非常适合电大尺寸结构的辐射与散射问题，依靠Feko软件的高性能进行计算，在保证精度的前提下能够极大降低工作量。最后设置对应频率的激励源与远场参数进行求解，具体参数参考表2。

表2 仿真参数配置

4.2  结果比较

为了对比不同材质粗糙面的远场散射特性和相同材质粗糙面的远场散射特性，对不同获取途径的粗糙面进行全波仿真，得到远场的散射电场分布如图5所示。比较图5（a）与图5（b），2个粗糙表面上的散射波瓣形状基本一致。对于粗糙表面而言，在该配置下尽管部分能量被散射到各个方向，但散射波瓣基本聚集在镜面反射方向周围。为更清楚地对比其散射电场分布情况，图6是测量得到的瓷砖粗糙面和生成得到的瓷砖粗糙面的入射面散射电场在笛卡尔坐标系的结果。

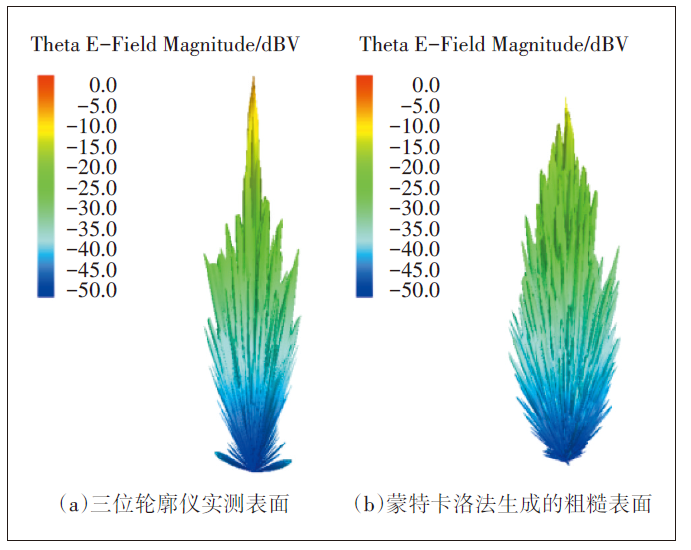
图5 粗糙面远场散射（3D）

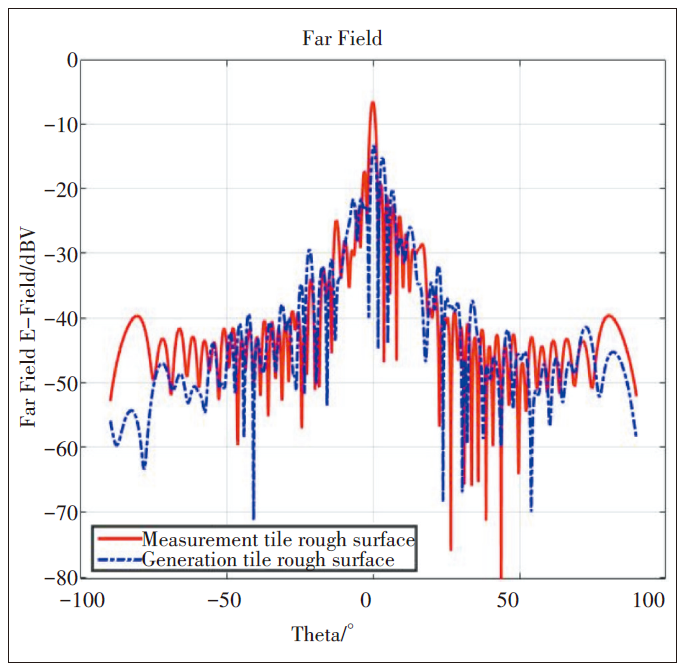
图6 测量瓷砖与生成瓷砖粗糙面远场

散射特性对比

首先，两者远场散射特性的包络曲线整体趋势变化大致相同，远场电场幅值在Theta为0时达到最大，随着Theta绝对值的增大逐渐减小；其次，两者的波瓣均为狭窄的陡峰，形状较为相似。这说明通过蒙特卡洛法重建的粗糙表面上散射电场的波瓣形状和变化趋势与实际表面基本相同，验证了用蒙特卡洛方法建立的理想粗糙面来代替实际粗糙面进行全波仿真的可行性。

0 5   

总  结

本文比较了由轮廓仪实际测量得到的粗糙表面和基于蒙特卡洛法建模生成的粗糙表面在太赫兹频段下的散射特性，通过测量的实际粗糙面与建立理想粗糙面的仿真对比，得到了如下结论。

a）实际粗糙面的高度分布服从正态分布，证明了基于蒙特卡洛方法对粗糙面进行建模的合理性。

b）通过对比2个粗糙面在相同频段下的散射电场分布，证明了使用蒙特卡洛方法建立的理想粗糙面以替代实际粗糙面来研究太赫兹频段粗糙表面散射特性的可行性。

对于未来太赫兹频段的研究，粗糙面的散射始终是一个重要的研究课题，理想粗糙面的仿真对于实际应用有很大意义［15］，在一些不便于实际测试的研究环境下，电磁计算仿真方法可以提供理想的测试环境，在一定程度上为实验提供可靠的数据。

       审核编辑 ：李倩