

浅析STAR-CCM+多重网格法
电子说
描述
随着网格尺寸的增加,雅可比、高斯-赛德尔或 ILU(不完全 LU)等传统迭代求解算法的收敛速度明显降低。 反过来,收敛缓慢会导致计算时间呈二次性增加。为加速求解器收敛,采用代数多重网格 (AMG) 法。多重网格法的概念基于以下事实:迭代求解算法可有效减少其波长对应于网格单元尺寸(高频误差)的数值误差分量。 但对于此类方法,长波长(低频)误差的降幅相当缓慢。
在连续粗糙化的线性系统的层次结构上,多重网格法通过迭代过程减少低频误差。代数多重网格衍生粗糙层方程组,而不参考基础网格几何。粗糙网格方程从精细网格系数的算术组合衍生得出。几次迭代之后,多重网格算法将计算从精细线性系统传递到粗糙线性系统。 这些迭代也称为平滑迭代,因为误差函数稍后将会平滑(即不含误差的高频分量)。
由于求解过程传递到更粗糙的线性系统,因此误差现在相对网格单元尺寸而言频率增高并可有效减少。 在更粗糙的线性系统上,为减少精细线性系统求解的误差,定义了缺陷方程。多重网格算法采用以下步骤:
- 聚结网格单元,形成粗糙网格级别。
- 将残差从精细级别传递到更粗糙的级别(称为限制)。
- 将校正从粗糙级别传递回更精细的级别(称为延长)。
-
多重网格循环
多重网格方法支持通过在粗糙网格序列上使用简单校正扫掠,显著加速高斯-赛德尔等基本迭代格式的运行。粗糙级别访问策略可能会对该算法的效率产生很大的影响。AMG中有两个循环策略,即固定和可变:
-
固定循环
完整的多重网格循环表示递归应用由以下步骤组成的单一循环:
- a) (预)平滑;
- b) 限制;
- c) 再循环;
- d) 延长;
- e) (后)平滑。
这些步骤将应用于一系列连续粗糙化的网格或方程组。平滑表示将任意数量的迭代松弛扫掠应用于当前精细级别上的方程,计算一组新校正。限制是指将现有残差向下传递到应用了新循环的下一个最粗糙级别。随后,结果校正将延长,即传递回同样应用了平滑的当前精细级别。有以下三种类型的固定循环:
- F 固定循环
- V 固定循环
- W 固定循环
- 可变循环
对于非刚性线性系统,此类循环是一种更经济的循环策略。每次在给定网格级别上扫掠后都会监视残差,而非按规则模式使用所有多重网格级别。如果残差减少率超出给定阈值,会继续在更粗糙的级别上求解。如果给定级别上的残差降幅超过指定阈值,则求解将转到更精细的级别。任何级别允许的扫掠数将进一步受到限制。
V 循环
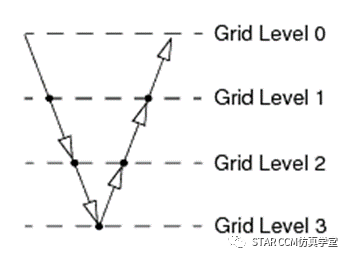
V 循环是最简单的固定循环类型,只有两个分支。 在第一个分支中,用户对最精细的级别执行大量松弛扫掠并将残差传递到下一个级别。 然后,对粗糙级别相继重复该操作,直至达到最粗糙的级别为止。粗糙“网格”通常仅包含几个“网格单元”。在最粗糙的级别上完成扫掠之后,使用得到的解校正下一个更精细级别上的求解。先在该级别执行一些松弛扫掠,然后重复此过程,直至达到最精细的级别为止,图 显示了此过程。
W 循环
对于刚性方程组,V 循环有时不能满足需要,进行更多粗糙迭代非常有用。W循环会增加粗糙松弛扫掠数,如图 所示。

F 循环
F循环是W循环的一种变体,此循环如图示,涉及的粗糙级别扫掠数少于W循环,但仍多于 V 循环。

-
基于贪婪算法的配电网网格负荷预测与规划2023-09-22 883
-
网格和密度的聚类算法在CRM中的应用2009-01-01 621
-
基于多重网格方法的快速电源网格分析法2009-05-06 727
-
网格划分原理与实例2010-09-11 697
-
基于网格法的NURBS自由曲线速度场规划2017-01-07 766
-
奇异摄动问题的移动网格算法2018-01-03 636
-
多重网格格子Boltzmann方法2018-01-24 793
-
基于数据驱动的任务并行多重网格应用2021-05-13 813
-
可提高网格建模的非线性引导滤波算法2021-06-03 730
-
从零开始学Star-CCM+仿真与应用2022-10-19 6225
-
STAR-CCM+中K-Epsilon湍流模型应用建议2023-05-19 6895
-
Simcenter STAR-CCM+流体仿真软件2024-11-12 3435
-
【Simcenter STAR-CCM+】通过快速准确的CFD仿真加速空气动力学创新2024-12-27 1996
-
【Simcenter STAR-CCM+】通过真实条件下的多物理场CFD仿真提高产品性能2025-03-12 772
全部0条评论

快来发表一下你的评论吧 !

