

浅谈卷积神经网络中的平移等变性映射
人工智能
描述
卷积神经网络(CNN)具有平移等变性的观点在某种程度上深入人心,但很少有人去探寻其原因或者理论根据。这篇文章将对这个问题进行系统地讲解,为后续进一步研究CNN的其他等变性和不变性设计夯实基础。
介绍
在机器学习中,我们通常关注模型的灵活性。我们希望知道选择的模型实际上能够完成我们想要的任务。例如,神经网络的通用逼近定理使我们相信神经网络可以近似任何所需精度的广泛类别的函数。但完全的灵活性也有缺点。虽然我们知道我们可以学习目标函数,但也存在许多错误的函数,它们在我们的训练数据上看起来完全一样。如果我们是完全灵活的,我们的模型可能会学习其中任何一个函数,一旦我们移开了训练数据,我们可能无法进行泛化。因此,需要对网络的灵活性加以限制。卷积神经网络是减少灵活性的一个著名成功案例。相较于早期的MLP网络,CNN的卷积牺牲了一部分灵活性,但实现了图像数据的平移等变性,这对于图像处理是十分重要的性质。
什么是平移等变性映射
简而言之,等变性映射是保留变换的代数结构的映射。作为一个特殊情况,平移等变映射是一种映射,当输入被平移时,会导致一个映射发生相应的平移,如下图所示:
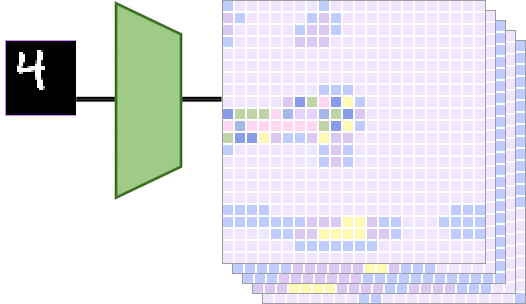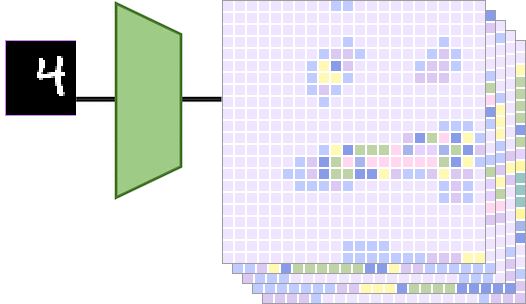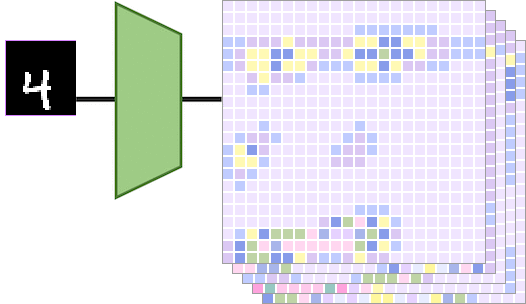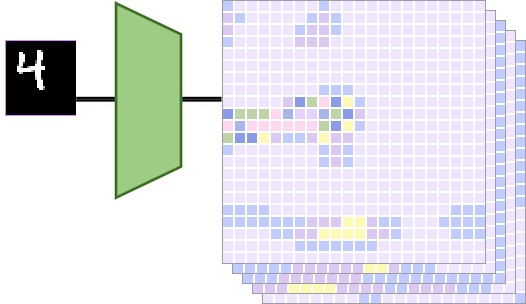
当左边的输入图像被平移一定的量时,输出特征图也会被相同的量进行平移。具体而言,如下图所示,
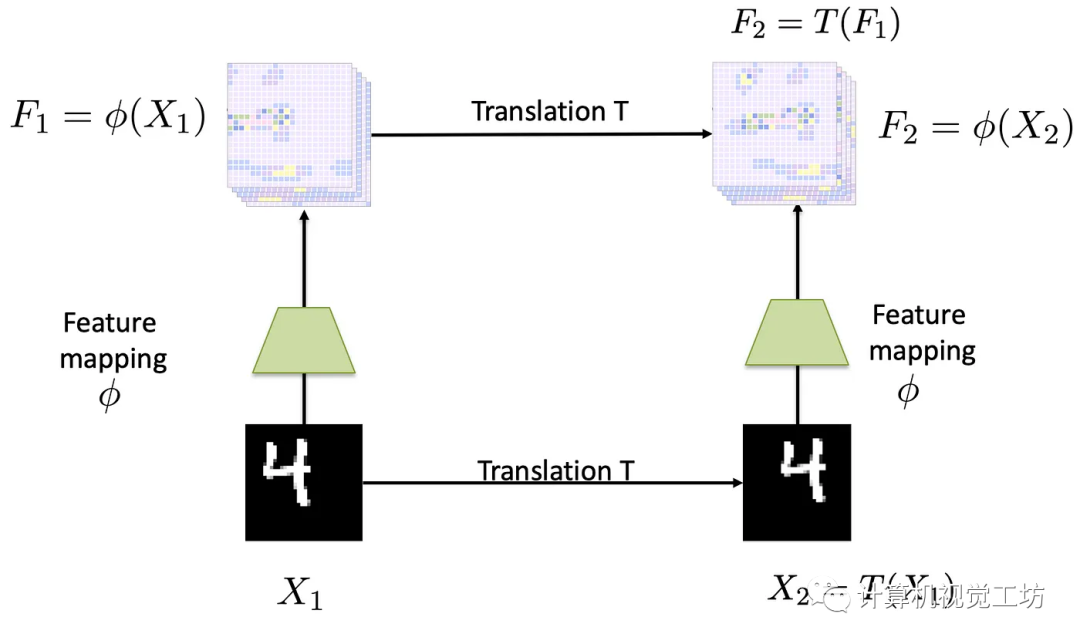

输入图像显示数字“4”,向右平移得到另一个输入图像。和分别是通过平移等变映射计算得出的特征图。在这种情况下,通过将传递给得到的特征图相当于对特征图做相同的平移得到的特征图。
卷积的平移等变性证明
首先让我们写下卷积的定义:
本质上,这定义了一个相关性(Correlation)而不是卷积(Convolution)。然而,在深度学习领域中的惯例是将其称为卷积,这里我们将沿用这个惯例。在这里,和都有个通道。为了简洁,本文中我们取。
现在,我们的目标是,给定一张图像,我们将用滤波器对其进行卷积。然后,我们想验证对于任何平移,以下两个操作是相同的:
将平移,然后将结果与进行卷积。
将与进行卷积,然后将结果平移。
编辑:黄飞
-
卷积神经网络的基本概念、原理及特点2024-07-11 3094
-
卷积神经网络通俗理解2023-11-26 1846
-
卷积神经网络的应用 卷积神经网络通常用来处理什么2023-08-21 6128
-
卷积神经网络原理:卷积神经网络模型和卷积神经网络算法2023-08-17 2201
-
卷积神经网络简介:什么是机器学习?2023-02-23 25380
-
卷积神经网络模型发展及应用2022-08-02 13209
-
卷积神经网络一维卷积的处理过程2021-12-23 1789
-
卷积神经网络的优点是什么2020-05-05 3538
-
什么是图卷积神经网络?2019-08-20 2318
-
卷积神经网络如何使用2019-07-17 2745
全部0条评论

快来发表一下你的评论吧 !

