Mahony算法常见的姿态融合算法

 

1 前言

Mahony算法常见的姿态融合算法，根据加速度计、陀螺仪、以及磁力计，融合计算机体四元数，计算速度快、精度较高。本文介绍六轴融合，即根据加速度计和陀螺仪数据，计算姿态。
我们需要计算的是机体的姿态。计算角度可以通过角速度积分，也可以通过加速度正交分解，但这两种方法都存在缺陷。角速度的误差会随着积分不断增大，而加速度存在高频噪声，因此希望融合两种数据。

2 算法

2.1 重力对齐误差

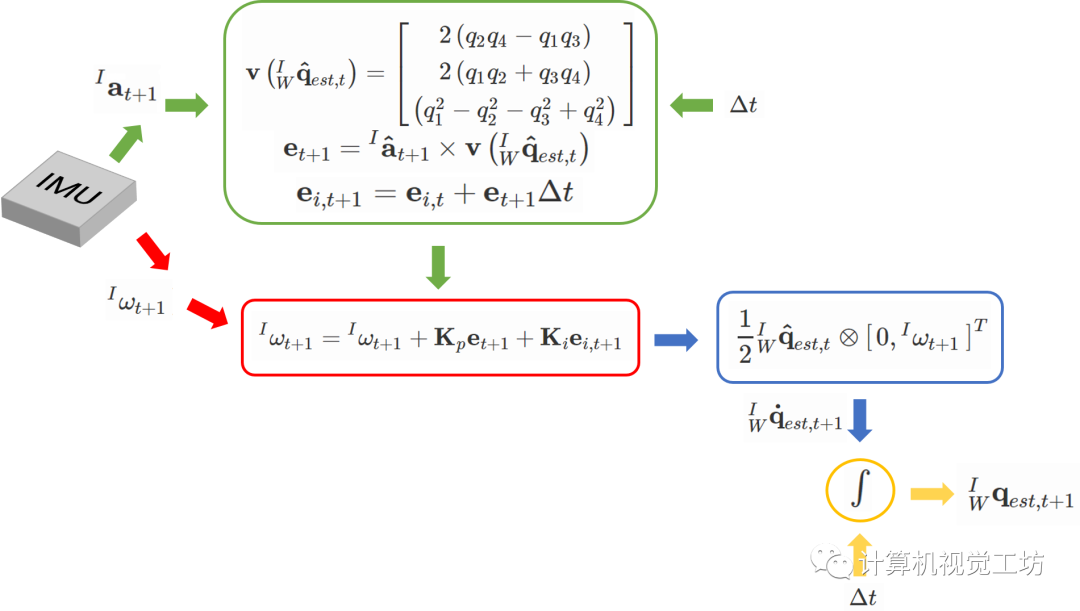
首先要指出的是，Mahony算法假设加速度计测量的加速度完全由重力提供，即物体本体运动产生的加速度可忽略不计。在这一假设下，我们假设当前时刻机体的姿态为，则将重力向量的表示转到机体坐标系下，应该为：，这里表示四元数对应的旋转矩阵：

进一步地，带入，得到

我们计加速度计测量得到的加速度，如果此时没有误差，应该有，但实际两个向量并不重合，存在一定的误差 。

为表示出，可以利用向量的叉乘：。因为叉乘的定义为：，当归一化为单位向量时，反应的就是角度。这里更准确的写为，下一时刻{t+1}时的误差为：

其中 为根据当前{t}时刻估计的角度四元数。再记这个误差的积分量为：

误差的积分量也参与了后续计算。

2.2 角速度融合

此时已经计算出加速度计观测出的误差了，记陀螺仪提供的角速度为，则把陀螺仪角速度的误差加上上述的误差，采用控制中常用的比例-积分控制器思想，

得到纠正的角速度。

讨论：为什么用叉乘？

陀螺仪由于本身精度问题，测量的角速度存在误差，在积分过程中这个误差会一直累加，我们要做的就是去消除或是补偿这个误差，因为加速度计长期的测量值是准确的，所以可以用加速度计来进行修正。如何找到一个另一个角速度量纲的值来修正陀螺仪的角速度值呢？这里明明只有陀螺仪可以测量角速度！这时候前面提到的向量叉积得到的误差向量就帮上大忙了，这个误差向量不就是反映出了角度变化量吗。算法巧妙的将加速度相关量转化为角度相关量，因而可以用这个角度值乘一个系数来修正陀螺仪的角速度，因为在偏差角度很小的情况下，我们可以将陀螺仪角速度误差和加速度计求得的角度差看做正比的关系，也就说明陀螺仪积分误差和向量叉积存在正比关系。[2]

欢迎关注微信公众号「3D视觉工坊」，加群/文章投稿/课程主讲，请加微信：QYong2014，添加时请备注：加群/投稿/主讲申请

方向主要包括：3D视觉领域各细分方向，比如相机标定|三维点云|三维重建|视觉/激光SLAM|感知|控制规划|模型部署|3D目标检测|TOF|多传感器融合|AR|VR|编程基础等。

2.3 计算下一时刻四元数

此时我们已经获取了下一时刻纠正后的角速度 ，这时候需要计算下一时刻的角度。
我们知道[3]四元数对时间的导数与角速度的关系为 ，即有

此时，再采用欧拉积分[4]，即可得到下一时刻姿态与当前时刻姿态的关系：

从而完成了下一时刻姿态的计算。

3 核心代码解析

我们以Matlab代码为例，结合上述内容进行介绍：

 

function obj = UpdateIMU(obj, Gyroscope, Accelerometer)
    q = obj.Quaternion;             % 当前时刻的四元数
    % 归一化加速度计测量数据
    if(norm(Accelerometer) == 0), return; end   % handle NaN
    Accelerometer = Accelerometer / norm(Accelerometer); % normalise magnitude

    % 计算重力在当前四元数位姿下的分量，即上述公式(2)
    v = [2*(q(2)*q(4) - q(1)*q(3))
            2*(q(1)*q(2) + q(3)*q(4))
            q(1)^2 - q(2)^2 - q(3)^2 + q(4)^2];

    % 计算重力分量与加速度计的测量误差，上述公式(3)
    e = cross(Accelerometer, v); 
    if(obj.Ki > 0)
        obj.eInt = obj.eInt + e * obj.SamplePeriod;     % 计算误差的积分，公式(4)
    else
        obj.eInt = [0 0 0];
    end
    
    % 角速度融合，公式(5)
    Gyroscope = Gyroscope + obj.Kp * e + obj.Ki * obj.eInt;            
    
    % 公式(6)
    qDot = 0.5 * quaternProd(q, [0 Gyroscope(1) Gyroscope(2) Gyroscope(3)]);

    % 欧拉积分计算下一时刻四元数，公式(7)
    q = q + qDot * obj.SamplePeriod;
    obj.Quaternion = q / norm(q); % 结果归一化
end

 

4 完整代码获取

官方C++/Matlab/C#代码：https://x-io.co.uk/open-source-imu-and-ahrs-algorithms/
官方python代码：https://github.com/xioTechnologies/Fusion/tree/main/Python
第三方python姿态解算库：https://ahrs.readthedocs.io/en/latest/filters/mahony.html

　　

      审核编辑：彭静