你需要了解的RC放电电路

在之前的RC 充电电路教程RC常数的影响及充电电路中，我们了解了电容器如何通过电阻器充电，直到达到等于 5 个时间常数(称为 5T)的时间量。然后，只要对其施加恒定电源，它就会保持充满电。

如果这个充满电的电容器现在与其直流电池电源电压断开，则在充电过程中积累的存储能量将无限期地保留在其极板上(假设是理想电容器并忽略任何内部损耗)，保持电压存储在其连接两端终端在一个恒定的值。

如果电池被短路更换，当开关闭合时，电容器会通过电阻R自行放电，因为我们现在有一个 RC 放电电路 。当电容器通过串联电阻放电时，电容器内部存储的能量被提取，电容器两端的电压Vc衰减到零，如下所示

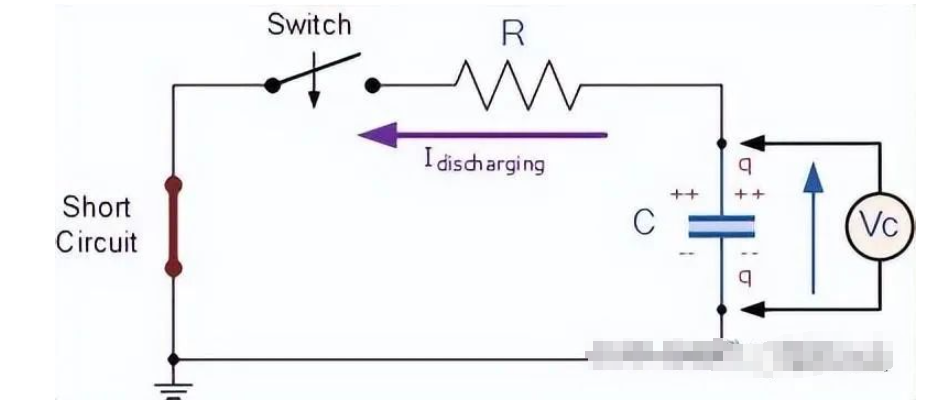
RC放电电路

正如我们在上一教程中看到的，在RC 放电电路中，时间常数 ( τ ) 仍然等于63%的值。然后对于最初充满电的 RC 放电电路，经过一个时间常数1T后电容器两端的电压下降了其初始值的63%，即1 – 0.63 = 0.37或其最终值的37% 。

因此，电路的时间常数表示为电容器放电至其充满电值的63%以内所需的时间。因此，RC 放电电路的一个时间常数为板两端的电压，代表其最终值的 37%，其最终值为0(完全放电)，在我们的曲线中，它给出为0.37Vs。

当电容器放电时，它不会以恒定速率失去电荷。在放电过程开始时，电路的初始条件为：t = 0、i = 0和q = Q。电容器极板上的电压等于电源电压且V C = V S。由于电容器板两端的电压在 t = 0 时处于最高值，因此最大放电电流流过 RC 电路。

RC 放电电路曲线

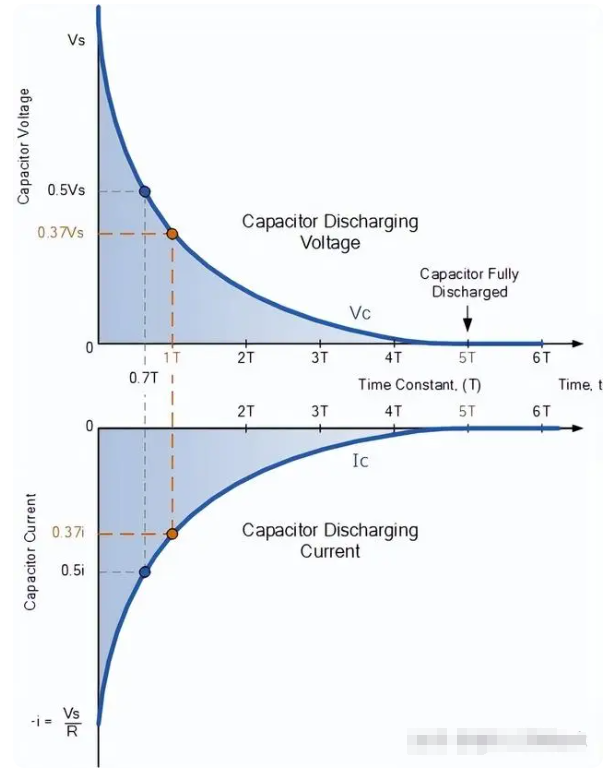
当开关第一次闭合时，电容器开始放电，如图所示。RC 放电曲线的衰减率在开始时比较陡峭，因为放电率在开始时最快，但随后随着电容器以较慢的速度释放电荷而呈指数下降。随着放电的继续，VC降低，导致放电电流减少。

我们在前面的 RC 充电电路中看到，电容器两端的电压C在0.7T时等于0.5Vc ，最终在5T时达到稳态完全放电值。

官方的

电容俩端随时间增加后的残留电压：

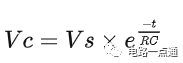
电容器完全充电至 10 伏。计算开关首次闭合时以下 RC 放电电路的RC 时间常数τ 。

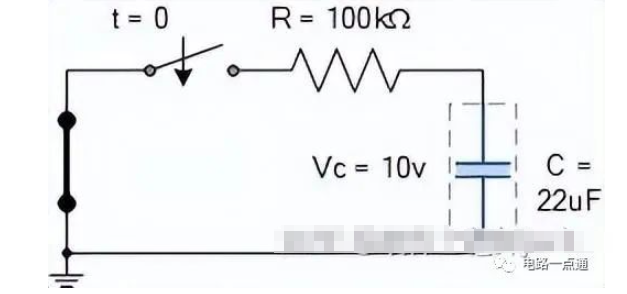
时间常数τ可使用公式T = RC以秒为单位计算得出。

因此时间常数τ给出如下：T = RC = 100k x 22uF = 2.2 秒

a)时间常数为 0.7 时电容器两端的电压值是多少?

在 0.7 时间常数 ( 0.7T ) 时，Vc = 0.5Vc。因此，Vc = 0.5 x 10V = 5V

b) 1 个时间常数后电容器两端的电压值是多少?

在 1 个时间常数 ( 1T ) 时，Vc = 0.37Vc。因此，Vc = 0.37 x 10V = 3.7V

c)电容器自身“完全放电”需要多长时间，(等于 5 个时间常数)

1 时间常数 ( 1T ) = 2.2 秒。因此，5T = 5 x 2.2 = 11 秒

审核编辑：汤梓红