排序算法之“归并算法”介绍

在说这个题目之前先来说说一个排序算法 “归并算法”

归并算法采取思想是分治思想，分治思想简单说就是分而治之，将一个大问题分解为小问题，将小问题解答后合并为大问题的答案。乍一看跟递归思想很像，确实如此，分治思想一般就是使用递归来实现的。但是需要注意的是：递归是代码实现的方式，分治属于理论。接下来看一副图理解下：

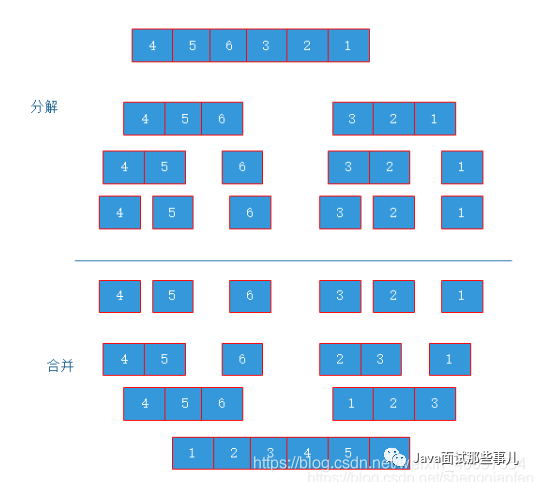
说完它的思想：我们再来分析下时间复杂度。归并算法采用的是完全二叉树的形式。所以可以由完全二叉树的深度可以得知，整个归并排序需要进行log2n次。

然后每一次需要消耗O{n}时间。所以总的时间复杂度为o{nlog2n}。归并排序是一种比较占用内存，但是效率高且稳定的算法

贴上代码：

 

static void Main(string[] args)
        {
            int[] arr = new int[] { 14,12,15,13,11,16 ,10};
 
            int[] newArr = Sort(arr, new int[7], 0, arr.Length - 1);
            for (int i = 0; i < newArr.Length - 1; i++)
            {
                Console.WriteLine(newArr[i]);
            }
 
            Console.ReadKey();
        }
 
        public static int[] Sort(int[] arr, int[] result, int start, int end)
        {
            if (start >= end)
                return null;
            int len = end - start, mid = (len >> 1) + start;
            int start1 = start, end1 = mid;
            int start2 = mid + 1, end2 = end;
            Sort(arr, result, start1, end1);
            Sort(arr, result, start2, end2);
            int k = start;
            //进行比较。注意这里++是后执行的，先取出来数组中的值然后++
            while (start1 <= end1 && start2 <= end2)
                result[k++] = arr[start1] < arr[start2] ? arr[start1++] : arr[start2++];
            //将每个分组剩余的进行复制
            while (start1 <= end1) 
                result[k++] = arr[start1++];
            //将每个分组剩余的进行复制
            while (start2 <= end2)
                result[k++] = arr[start2++]; 
            for (k = start; k <= end; k++)
                arr[k] = result[k];
            return result;
        }

 

说完了归并算法回到题目上来 首先分析下 题目给定的是两个已经排好序的数组合并，关键字“合并”，“两个”，正好符合我们的归并算法，并且已经分类好了，只需要去合并就可以了。

来看下几张图。

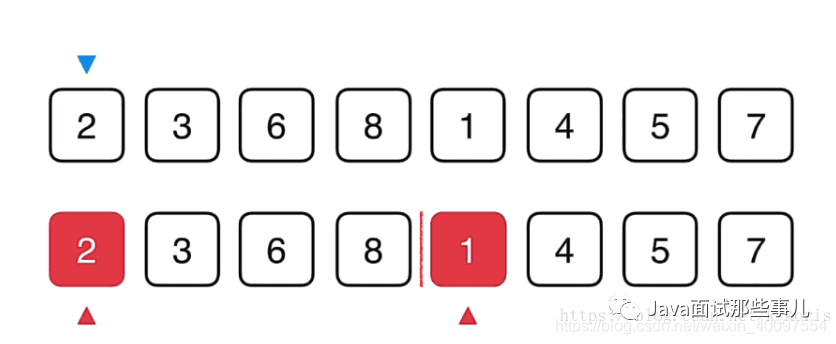
蓝色的箭头表示最终选择的位置，而红色的箭头表示两个数组当前要比较的元素，比如当前是2与1比较，1比2小，所以1放到蓝色的箭头中，蓝色的箭头后移，1的箭头后移。

然后2与4比较，2比4小那么2到蓝色的箭头中，蓝色箭头后移，2后移，继续比较.......

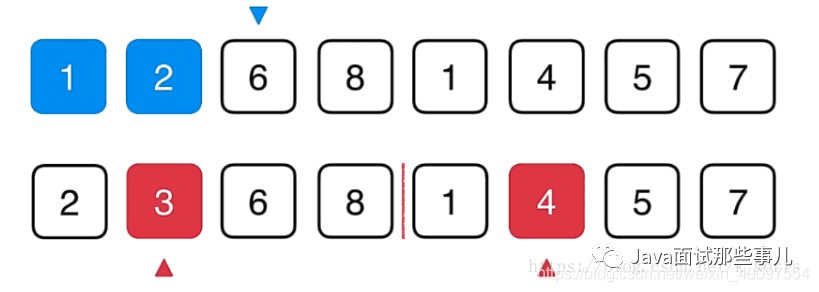
归并思路就是这样了，最后唯一需要注意的是那个先比较完的话，那么剩下的直接不需要比较，把后面的直接移上去就可以了，这个需要提前判定一下。 

贴上代码：

 

static void Main(string[] args)
        {
            int[] arr1 = new int[] { 2, 3, 6, 8 };
            int[] arr2 = new int[] { 1, 4, 5, 7 };
            int[] newArr = Sort(arr1, arr2);
            for (int i = 0; i < newArr.Length - 1; i++)
            {
                Console.WriteLine(newArr[i]);
            }
 
            Console.ReadKey();
        }
 
        public static int[] Sort(int[] arr1,int[] arr2)
        {
            int[] newArr = new int[arr1.Length + arr2.Length];
            int i = 0, j = 0, k = 0;
            while (i < arr1.Length && j < arr2.Length)
            {
                if (arr1[i] < arr2[j])
                {
                   
                    newArr[k] = arr1[i];
                    i++;
                    k++;
                }
                else
                {
                    
                    newArr[k] = arr2[j];
                    j++;
                    k++;
                }
            }
 
            while (i < arr1.Length)
                newArr[k++] = arr1[i++];
            while (j < arr2.Length)
                newArr[j++] = arr2[j++];
            return newArr;
        }
    }

 

 

　　

      审核编辑：彭静