光学系统的空间像原理

  实际上，许多光学系统是把空间的物点成像在一个像平面上，称为平面上的空间像，如望远物镜、照相物镜等属于这一类。 空间中的物点分布在距离光学系统的入射光瞳不同的距离上，这些点的成像原则与平面物体的成像相同。

如图1所示，B1,B2,B3,B4为空间的任意点，点P为入射光瞳中心，点P'为出射光瞳中心，A'B'为像平面，称为景像平面。在物空间与景像平面相共轭的平面AB称为对准平面。

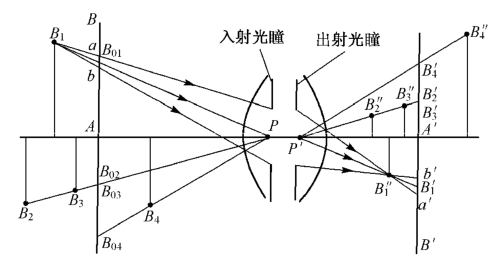
图1：光学系统的空间像示意图 点B1,B2,B3,B4与入射光瞳中心点P的连线分别为这些点的主光线。这些点在像空间的共轭点分别为B1″,B2″,B3″,B4″。通过这些点的主光线与景像平面A'B'分别交于点B1',B2',B3',B4'。

显然，位于同一主光线B2P上的两点B2和B3在景像平面上的对应点B2'和B3'重合在一起。因此，点B2和B3与点B2'和B3'在对准平面上的主光线方向的投影相共轭。

所以空间点在平面上的像可以这样得到：以入射光瞳中心点P为透视中心，即以点P为投影中心，将空间点B1,B2,B3,B4沿主光线方向向对准平面上投影，则投影点在景像平面上的共轭点B1',B2',B3',B4'便是空间点的平面像。

当光瞳有一定大小时，由点B1发出的充满入射光瞳的光束与对准平面交为弥散斑a'b'，在景像平面上的共轭像也是一个弥散斑ab，为空间像点B1″在景像平面上的投影。

同理，所有位于景像平面以外的空间点都可在对准平面上产生一个弥散斑，同样在景像平面A'B'也可得到其共轭像。

由图1可知，ab或a'b'的大小与入射光瞳的直径有关，入射光瞳的直径减小，这些弥散斑也随之减小。当入射光瞳的直径小到一定程度时，弥散斑ab可看作一个点，其共轭像αb'也可看作一个点。

同样对于点B2,B3,B4在景像平面上得到的弥散斑也由于入射光瞳减小而可认为是点像B2',B3',B4'，因而可以在景像平面A'B'上得到对准平面以外空间点的清晰像。

如上所述，物方空间点成像相当于以入射光瞳中心为投影中心，以主光线为投影线，使空间点投影在对准平面上，再成像在景像平面上。

或者在像空间以出射光瞳中心为投影中心，各空间像点沿主光线投影在景像平面上，也可形成空间物点的平面像。

如果入射光瞳位置相对于物方空间点（即景物）位置发生变化，则景像也随之变化。

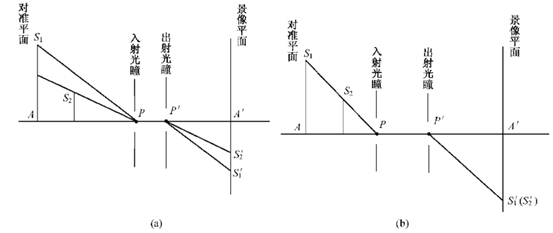
  图2：入射光瞳位置变化形成透射失真的示意图

如图2所示，同样的景物在图2(a)中S1'和S2'是分开的：而图2(b)中由于入射光瞳位置的变化，S1'和S2'重合在一起。显然，投影中心前后移动，投影像的变化和景物是不成比例的，这种现象叫做透视失真。

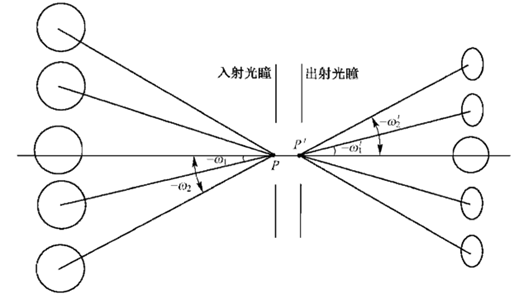
  图3：广角物镜拍摄球状物体时产生的景像变形

用广角物镜拍摄物体时，若物体为一系列球状体，如图3所示，它们对入射光瞳中心均张以相同的圆锥状立体角，顶点为入射光瞳中心，这些圆锥状光束的共轭光束也为圆锥状。每一个圆锥状光束的轴线以不同的角ω'交于景像平面，ω'的最大值为物镜像方全视场角的一半。由图3可知，锥状光束在景像平面上的截面将随ω'的不同而不同，该现象称为景像畸变，圆形变成椭圆形，越在视场边缘，这种现象越严重。  

　　

      审核编辑：彭静