

时序逻辑电路设计之同步计数器
描述
时序电路的考察主要涉及分析与设计两个部分,上文介绍了时序逻辑电路的一些分析方法,重点介绍了同步时序电路分析的步骤与注意事项。 本文就时序逻辑电路设计的相关问题进行讨论,重点介绍时序逻辑电路的核心部分——计数器。
计数器的分类
所谓计数器,就是在技术脉冲的驱动下,一次进行加1或者减1计数的时序逻辑电路。 总体来说,由上文时序逻辑电路的分析中可以得知,时序逻辑电路包括同步电路与异步电路两种,因此计数器也要分为同步计数器和异步计数器,计数器又因计数顺序不同分为加法计数器与减法计数器,每种计数器的计数规则不同又出现了进制.... 这样的不同造成了在设计计数器时组合电路的设计与触发器的选型都有着很多的不同,因此熟悉各种类型的计数器时实现计数器设计的基础。
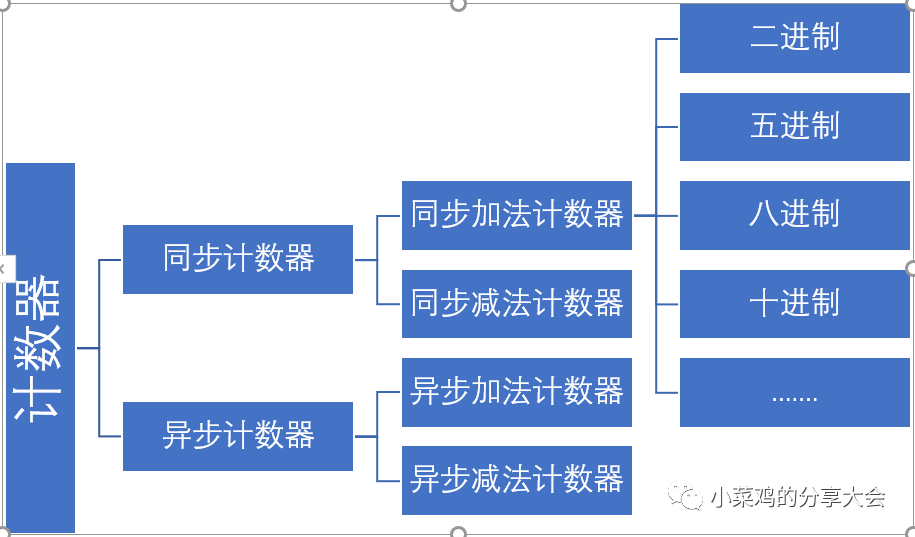
同步计数器
同步计数器的设计核心就是利用几个同步的触发器和一定的门电路将需求的真值表循环输出,这里需要注意的是,每一位数都是由一个触发器实现的,比如我要实现的是一个三位二进制数(也就是八进制),那么我一定需要使用3个触发器依次表示由高到低的三位数字,而且设计一定是由低位到高位进行,并且依据每一位的变化情况选择合适的触发器实现对应的功能, 因此选择触发器成了相当重要的一步。
从个人浅薄的设计经验来讲,一般的计数器都能够利用T触发器或D触发器来实现,并且相对于其他触发器能够达到最简的设计思路。 如果题目明确要求使用JK触发器,做法一是直接套用卡诺图化简的方法找每个JK对应的逻辑函数,然后利用JK触发器的特征方程搭建电路,二是把JK两端直接接在一起就成为了T触发器,这样的做法极大的简化了设计的过程,不需要繁琐的卡诺图化简和方程对应,其中便利可自行设计体会,如第七次实验内容的第三问。
同步三位二进制加法计数器
以三位二进制加法计数器为例进行简单的设计介绍,首先根据需求列真值表,这是设计所有计数器电路的第一步,如图
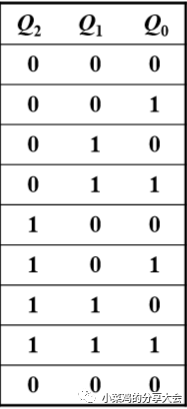
首先看Q0,很明显的观察到,每一个脉冲都会使Q0反转,也就是T'触发器的特性(这里直接体现了掌握各种触发器的特性的重要性,不熟练的小伙伴建议先去看看之前的关于触发器的几篇推文),所以第一个T'触发器的输出就是Q0。
接下来看Q1这一列,还是存在规律的反转,但是这里不要看他是每两个翻转一次这个事情,对于同步电路设计而言用处不大,而是要找这个反转和其他几个Q之间的关系,比如这里就是在Q0=1的情况下Q1才会反转。 在这里建议
一个暂时的设计原则:在同一个电路的设计当中,尽量所有的触发器都选择同样的一种,这样做的目的是减少思考量。 所以这里我们依然采用T触发器(T'就是T触发器的输入端T始终接1),那也就是说本来的T'触发器是来一个脉冲就要变化,现在的是要在Q0=1的时候再来脉冲才变化,所以就是在Q0=1的时候成为T'嘛,因此令T=Q0。
同理,我们看到真值表中的Q2只有在Q0和Q1同时为1的情况下才变化,所以T=Q1Q0,最后不要忘记进位端的设计,逢111进1,所以进位C=Q2Q1Q0.这样我们就完成了设计(因为这里没有无效态,所以不需要自启动检查)。 如图
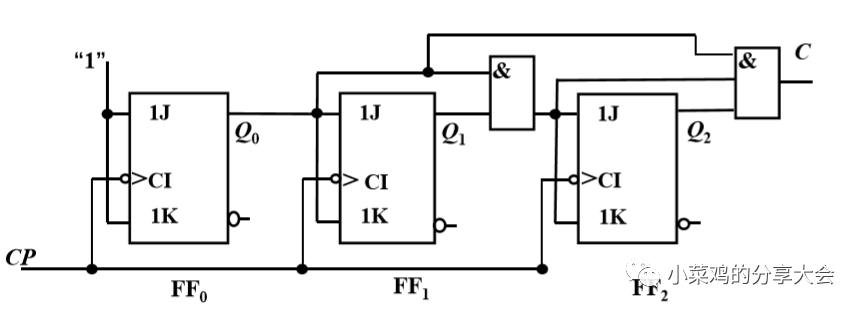
同步十进制加法计数器
上面介绍的三位二进制计数器正好满足了三位计数器所有的八个状态,即不存在无效态。 但是在很多的设计中,我们并不能使用所有的状态,存在的无效态我们需要将其跳过主循环并能够自启动,比如七进制,十进制,这里我们以十进制加法计数器作为例子进行介绍。
首先还是要列真值表,如图
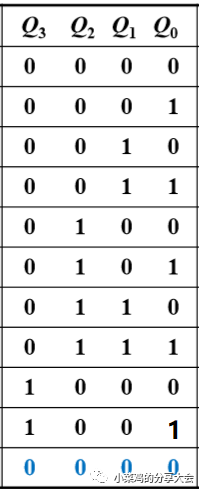
这里很明显的体现出来了状态的未完全使用。 四位二进制可以表述16个状态,即0000--1111,但是我们在这里只使用了前10位,即0000--1001,从1001直接回到0000,但是整体的设计思路和上一个没有很大的区别,仍然是从低位到高位依次设计。
首先观察到Q0依然是交替变化,所以仍然用T'。 其次Q1的大体变化仍然同上一个近似,不同点在于最后一个的变化,这时的Q0=1,但是Q1没有反转,这里需要意识到的是不仅仅需要看低位的现态,还要看别的位的现态,找到最特殊的点,这里的特殊点就是Q3=1,之前在Q1变化的时候Q3都是0,因此T1不简单的等于Q0,而同时要保证Q3=0,即为T1=Q0Q3(非)。 剩余两个依次类推。 方程与电路如下:
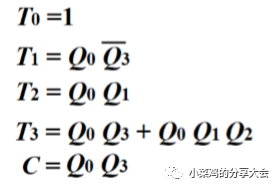
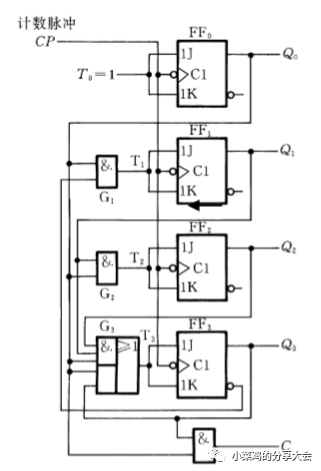
-
时序逻辑电路有哪些 时序逻辑电路和组合逻辑电路区别2024-02-06 13473
-
时序逻辑电路设计之计数器2023-05-22 6968
-
同步计数器和异步计数器是什么 同步计数器和异步计数器的主要区别?2023-03-25 29325
-
时序逻辑电路的精华——计数器2022-12-29 1812
-
计数器及时序电路2022-07-10 684
-
数字电路设计之同步时序逻辑电路2020-12-25 6444
-
时序逻辑电路分为几类2019-02-26 52336
-
时序逻辑电路的主要故障分析2018-04-09 6905
-
【FPGA开源教程连载】第三章 时序逻辑电路设计之计数器2016-12-21 5286
-
Multisim的时序逻辑电路设计仿真2012-02-10 2088
-
移位型计数器中反馈逻辑电路的设计2010-04-26 663
-
同步时序逻辑电路2009-09-01 1078
-
时序逻辑电路设计2009-03-20 5895
-
时序逻辑电路2008-09-24 3568
全部0条评论

快来发表一下你的评论吧 !

