

电驱动系统各传动轴轴承载荷工况的计算方法
电子说
描述
本文以常用汽车电驱动系统轴承为对象,首先分析了电驱动系统的结构特点,其次计算了电驱动系统中各传动轴的扭矩、转速以及轴承载荷;然后基于实际对象,运用MATLAB 语言,并采用Lundberg-Palmgren 模型计算了轴承疲劳寿命。最后采用疲劳损伤累积理论,计算分析了某电驱动系统轴承损伤,为电驱动系统的进一步研究提供可靠基础。
1 电驱动系统结构
常用汽车电驱动系统为“电机轴-输入轴-中间轴-输出轴”结构。工作中,电驱动系统以电机轴的转速和扭矩信号作为输入,再经过总成中减速器的输入轴、中间轴以及输出轴各轴的斜齿轮,降低转速增加扭矩,再通过输出轴输出。本文假设电机轴转速顺时针方向为正,即以前进挡位分析,其结构如图1 所示。
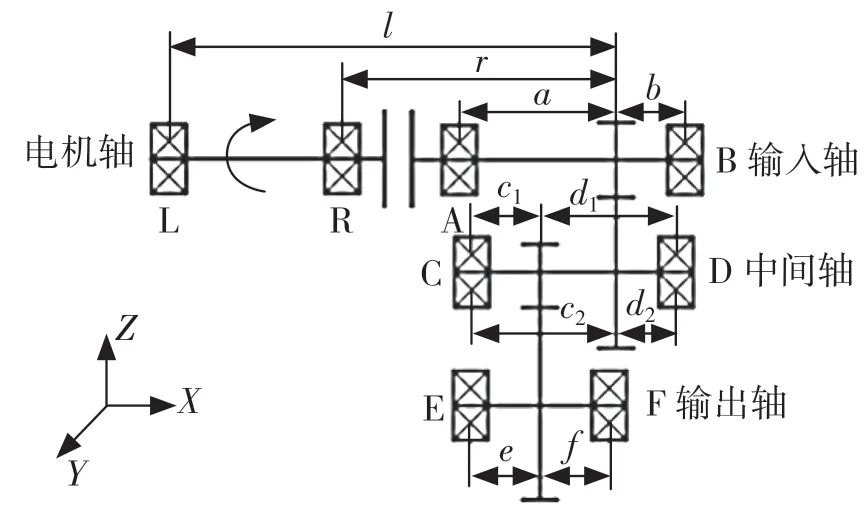
图1 汽车电驱动系统轴系结构简图
Fig.1 Structure diagram of shaft system of automobile electric drive system
图1 中,L 和R、A 和B、C 和D 以及E 和F分别表示电机轴、输入轴、中间轴以及输出轴上的左右端轴承,各轴承固定形式均为单向固定;l、r、a、b、c1、d1、c2、d2、e和f分别表示轴承与所在轴斜齿轮间的距离。
如图2 所示,轴系中各传动轴在空间上并不处于同一平面,这使得中间轴分别受到输入轴和输出轴斜齿轮两者的径向力不在同一方向上,所以在受力分解中间轴轴承的载荷时,需要首先考虑轴系各轴间的空间位置关系[3]。图2 中轴系空间位置角θ的表达式为
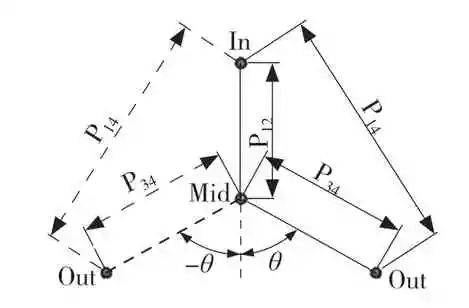
图2 汽车电驱动系统轴系空间位置简图
Fig.2 Spatial position diagram of shaft system of automobile electric drive system
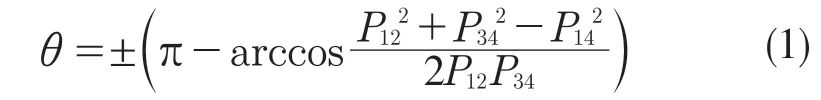
式中:P12,P14,P34——输入轴和中间轴、输入轴和输出轴以及中间轴和输出轴之间的空间距离。
2 轴承载荷计算 2.1 斜齿轮载荷计算
由于存在齿数比,轴承载荷计算需首先计算各个工况(轴上扭矩T、电机输出转速n)下斜齿轮的受力,才能进行载荷分配至轴承端。
斜齿轮圆周力Ft计算公式为

斜齿轮径向力Fr计算公式为
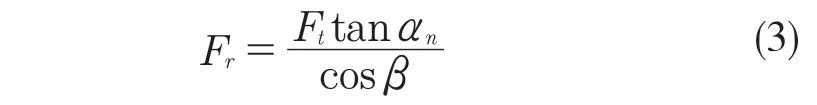
斜齿轮轴向力Fα计算公式为
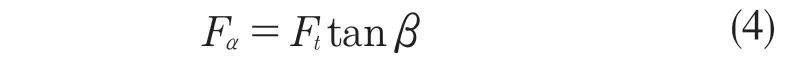
式中:T——该斜齿轮所在轴的扭矩,N·m;αn,d,β——斜齿轮压力角、节圆直径、螺旋角。
2.2 轴承载荷计算
2.2.1 电机轴轴承载荷计算
由于电驱动系统电机轴与输入轴常以联轴器相连,所以电机轴轴上扭矩为T,转速为n。忽略轴的挠曲对齿轮和轴承载荷的作用,电机轴轴承载荷主要考虑减速器输入轴斜齿轮所受扭矩作用,其轴承径向力由斜齿轮所受圆周力和径向力综合而成。由于连轴器的缓冲功能,认为电机轴上的两端轴承均不承受轴向力。电机轴轴承载荷如表1 所示。
表1 电机轴轴承载荷
Tab.1 Motor shaft bearing load

2.2.2 减速器轴系轴承载荷计算
由于齿数比,转速由电机轴传至输出轴会依次递增,而扭矩依次递增,各轴扭矩与转速如表2所示。基于力的平衡关系,可求出如表3 所示的减速器各传动轴轴承端所受载荷。
表2 减速器各传动轴扭矩转速
Tab.2 Torque and speed of each drive shaft of the reducer

表3 减速器各传动轴轴承载荷
Tab.3 Bearing load of each drive shaft of the reducer

其中,±或∓当T>0 时取上面符号,当T≤0 时取下面符号;{Ft;Fr;Fa}和{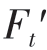 ;
;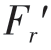 ;
;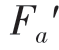 }分别表示斜齿轮1、2 和斜齿轮3、4 间的圆周力、径向力及轴向力;zx表示斜齿轮x的齿数。
}分别表示斜齿轮1、2 和斜齿轮3、4 间的圆周力、径向力及轴向力;zx表示斜齿轮x的齿数。
3 轴承疲劳寿命与损伤计算 3.1 轴承疲劳寿命计算
根据Lundberg-Palmgren 寿命理论[4,5],轴承疲劳寿命的基本计算公式为
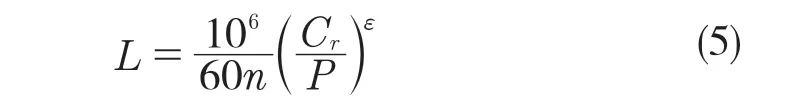
式中:C——径向基本额定动载荷;P——当量动载荷;ε——寿命指数,球轴承取3,滚子轴承取10/3。
轴承基本额定动载荷Cr以及当量动载荷P为
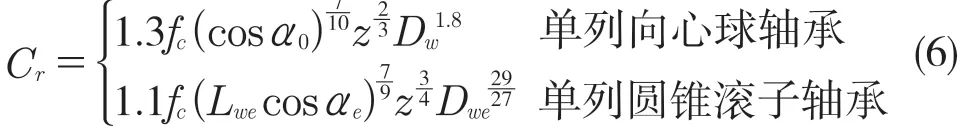
式中:fc——和轴承结构有关的修正系数[6];α0——球轴承接触角;αe——圆锥滚子轴承锥度角;z——滚动体数量;Dw——球轴承滚珠直径;Dwe——圆锥滚子轴承滚子等效直径;Lwe——滚子有效接触长度。
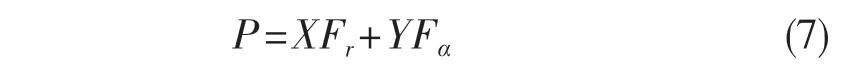
式中:X——径向动载荷系数;Y——轴向动载荷系数[6]。
3.2 轴承损伤计算
轴承疲劳失效为典型的损伤累积过程,在许多应用场合中,轴承承受随时间变化的循环载荷,而不是固定载荷,对于这类工况,可采用Palmgren-Miner 线性累计损伤法则[7,8]。
轴承在当量动载荷为P1的运转条件下,滚道的寿命L1,若在此工况下运转了N1转,则P1的运转条件下轴承的当量损伤为: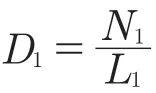 。若轴承经历一段随机道路载荷,依次在P1,P2,… ,Pn当量负荷作用下运转了N1,N2,… ,Nn转,则该随机道路载荷对轴承造成的损伤为:
。若轴承经历一段随机道路载荷,依次在P1,P2,… ,Pn当量负荷作用下运转了N1,N2,… ,Nn转,则该随机道路载荷对轴承造成的损伤为:
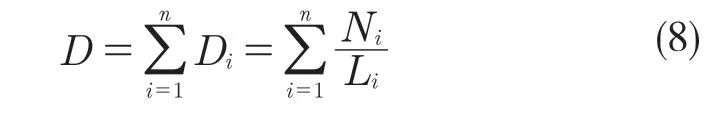
其中,n为轴承的一组运转条件,对应的每一种运转条件i,轴承所对应的疲劳寿命为Li转,但在此工作条件下轴承只运转了Ni转,Ni
4 实例分析
以某汽车电驱动系统总成为例,其轴系参数及轴承结构参数分别如表4 和表5 所示。
表4 电驱动系统轴系参数
表5 电驱动系统轴承结构参数
以图3 和图4 所示的实验场电机轴扭矩-转速载荷谱作为输入,将每1 s 作为一个稳态工况,即单个稳态工况下该轴承的损伤为
图3 电驱动系统电机轴转速载荷谱
图4 电驱动系统电机轴扭矩载荷谱
式中:n——该轴承所在轴的转速。
然后根据本文的计算方法,运用MATLAB 语言求解计算,各轴承损伤结果如图5 所示。
图5 电驱动系统轴承损伤计算结果
可以看出,轴承R、E 和F,即电机轴右端轴承和输出轴左右端轴承的损伤明显大于其他轴承。原因可能是电机轴承载的转速最高,且电机轴右端载荷比左端更大;而输出轴两端轴承虽然转速较低,但是承受载荷较大导致损伤较高,结果符合工况真实情况。
5 结论
本文总结了电驱动系统各传动轴轴承载荷工况的计算方法,且考虑到了轴系结构、空间位置的影响,具有较好的实用性和通用性,能够为电驱动系统轴承工况研究提供参考。
基于试验场载荷,结合L-P 和Miner 理论,计算了电驱动系统各传动轴轴承的疲劳寿命以及损伤。该方法充分考虑到汽车电驱动系统载荷谱的高随机性特点,能够为汽车电驱动系统轴承的选型、轴系结构优化等提供帮助。
本文未考虑轴承实际运行中会承受倾覆力矩,该力矩对轴承疲劳寿命有一定影响,因此对于电驱动系统轴承损伤的计算分析有待进一步研究。
Tab.4 Electric drive system shafting parameters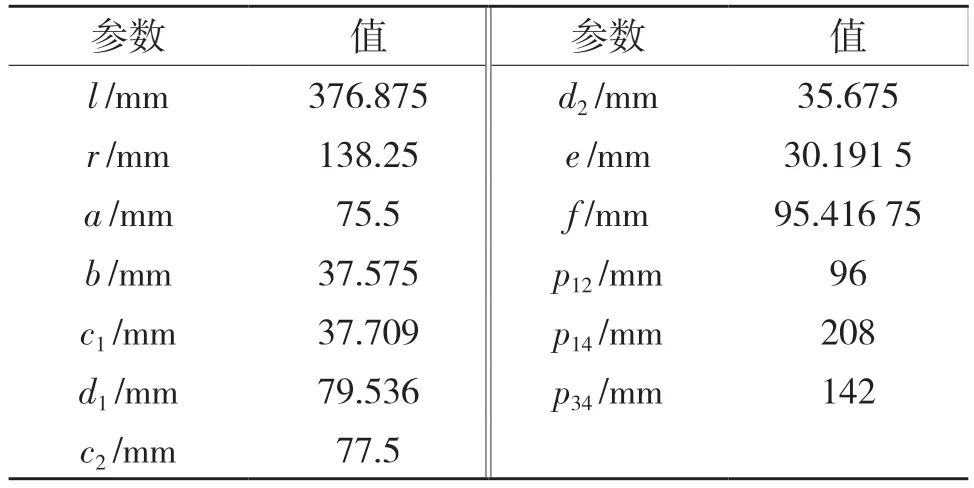
Tab.5 Electric drive system bearing structure parameters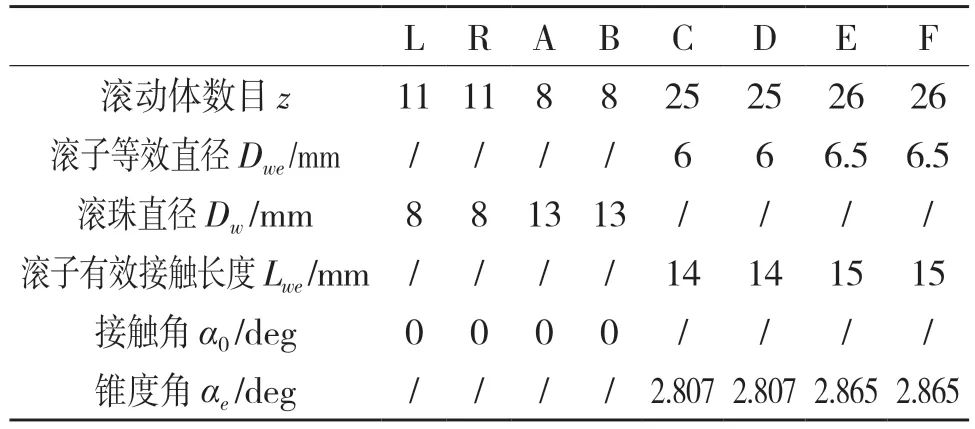
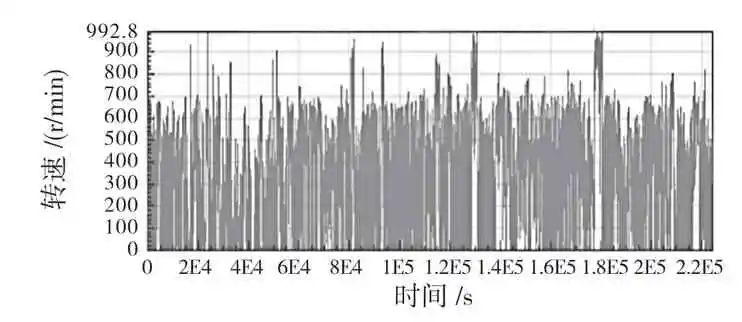
Fig.3 Motor shaft speed load spectrum of electric drive system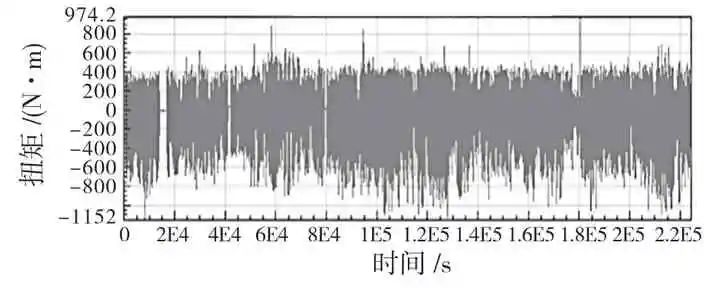
Fig.4 Torque load spectrum of electric drive system motor shaft
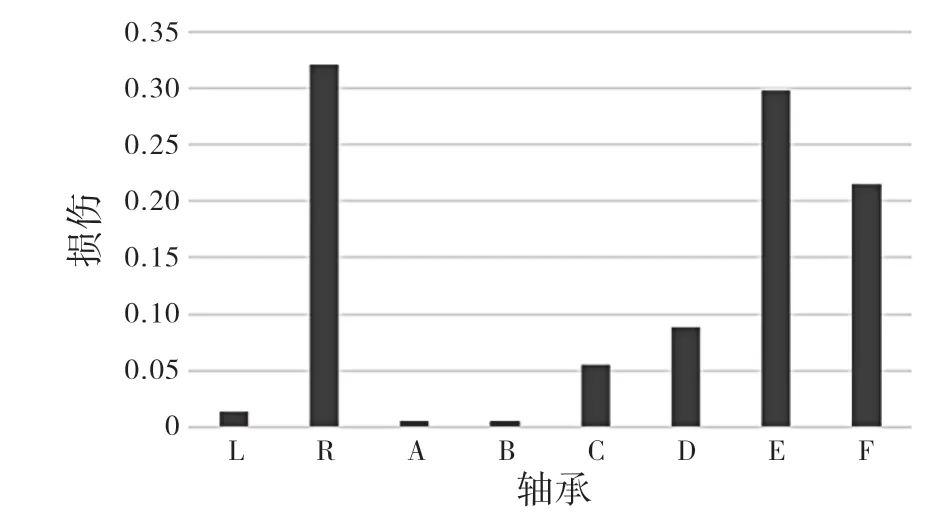
Fig.5 Calculation results of bearing damage of electric drive system
-
双电伺服主传动轴电机控制软件的开发研究2025-06-18 204
-
鄂破皮带轮传动轴磨损是如何修复的2024-02-04 455
-
浅析汽车传动轴结构、工作原理2023-10-23 2748
-
浅谈带式输送机传动轴磨损修补方法2023-05-22 505
-
传动轴磨损严重会怎样?怎么修补?2022-07-01 585
-
传动轴磨损的修补方法介绍2022-04-13 1403
-
压力机传动轴轴承位磨损原因及修复方法2021-06-04 1745
-
压力机传动轴轴承位磨损的修复工艺2021-04-14 946
-
修复碎煤机传动轴轴径磨损的方法是怎样的2021-03-21 885
-
汽车传动轴工作原理2019-11-04 10045
-
传动轴坏了有什么影响2018-10-22 47951
-
基于Cortex_M3的齿轮传动轴损伤动态监测系统的设计与实现2017-09-28 758
全部0条评论

快来发表一下你的评论吧 !

