最专业最全面天线原理汇总1

天线作为微波系统的重要组成部分，也应该成为每个通信工程师完善基础理论的重要一环，从公众号创建之初，目的就在于尝试建立更加完善、多元化的电磁知识体系，借此帮助读者在解决愈发复杂的系统问题时，能够多一份笃定与从容。

这篇文章将兼顾体系和细节，兼顾科普与专业，兼顾理论与实践，系统而通俗的介绍关于天线的种种，希望能够助力天线萌新入门进阶，辅助天线工程师查漏补缺。受限于作者专业和认知水平，文中所述如有偏颇，还请斧正。

2.内容涉及

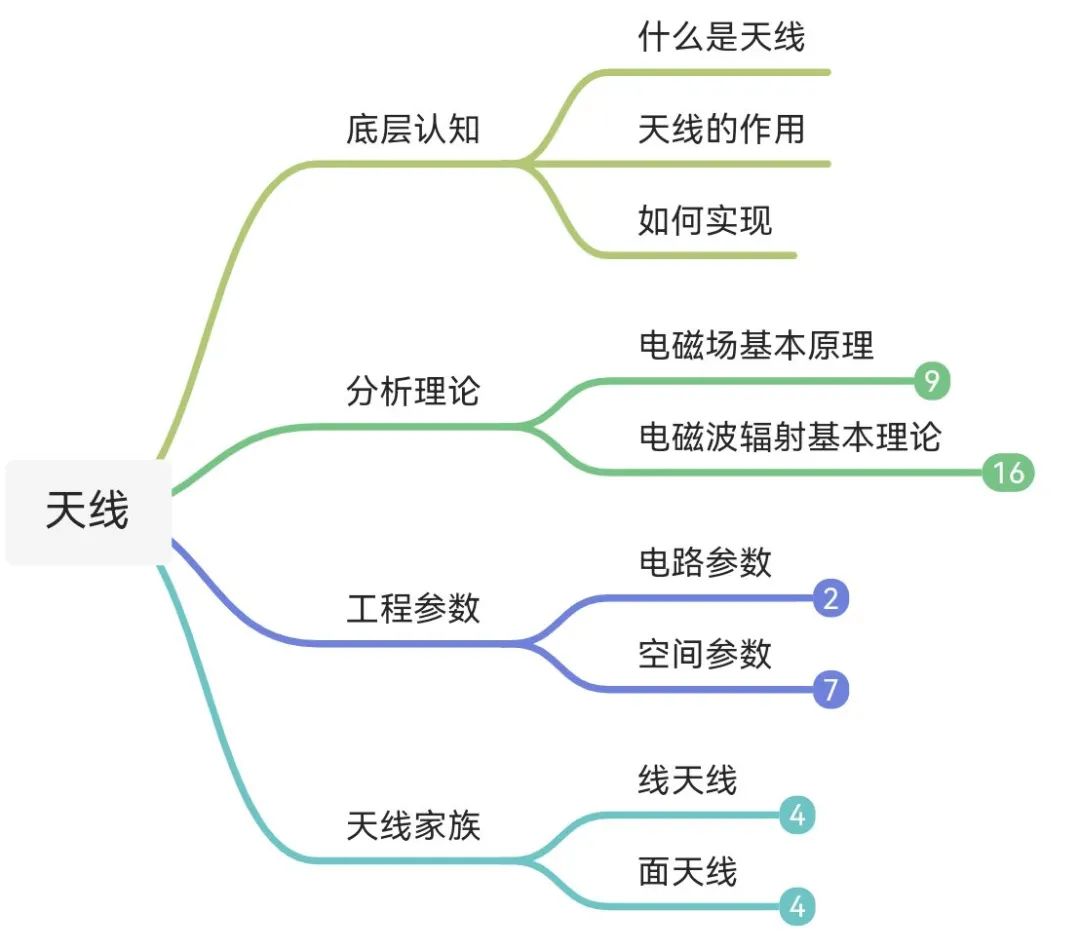
本文将从四个方面展开：

**1. 底层认知：**无论你是从事天线设计的工程师，还是仅仅对天线略感兴趣的门外汉，你应该对天线有一个最基本的认知：那就是“什么是天线？天线的作用是什么？其又是如何实现这样的作用的？”，其作为“底层认知”，是打开“天线世界”大门的钥匙；

**2. 分析理论：**天线作为一个发展有百余年历史、高度工程化的微波器件，它的分析和设计都离不开坚实的“数理基础”，这可分为两大理论群：

1）以maxwell方程为基础，结合系列引申原理，组成的电磁场的基本原理，其为一切电磁问题分析的基础；

2）以四种基本辐射单元分析理论构成的电磁波辐射基本理论，它们如同天线分析这座乐高大厦的积木块，极大的简化了分析过程；

**3. 工程参数：**什么样的设计才是好的设计，光靠“感性认知”可不行，你需要专业的评估参数以及量化的指标，该部分内容将介绍评估天线设计优劣的几种重要的工程参数，其包括天线作为微波系统终端的“电路参数”以及作为空间电磁波辐射始端的“空间参数”；

4. 天线家族： “分析理论”和“工程参数”的地基搭建好了后，我们就开始正式操刀分析一众天线的辐射特性和机理。文章依据天线结构特征，分为线天线和面天线两大类介绍八种常见天线的分析方法和辐射机理，分析将基于天线几个主要工程参数，并结合天线上电流及近场分布，将尽可能以最直观的方式展示每种天线的特点和辐射机理。

---

一、底层认知

在日常生活中，天线的身影随处可见，小至家用路由器、手机设备上的天线，大到通信基站甚至于射电望远镜的天线。天线可以被称为信息时代极为重要的组成部分。所以什么是天线？它有什么用？又是如何实现这些作用的？

各种常见天线

正如村头的广播喇叭是声音传输系统的终端，将电线中处于电信号状态的声音转换为空间自由传播的声波；又如神经树突是神经系统的终端，将神经细胞上的感觉电信号转换为自由状态的神经递质。 天线是微波系统的终端 ，通过将束缚于电缆上的微波信号转化为自由空间传播的电磁波，从而实现无线通信，它是 微波系统与自由空间的纽带 。

声音传输系统的终端

神经系统的终端

天线是微波系统的终端

不失一般性，我们以天线家族中较为简单的偶极子天线为例，介绍天线是如何将束缚状态的电磁波信号转换为自由辐射的电磁波信号。我们家里常用的路由器上面的几个天线通常就是偶极子天线的变种。

路由器天线

如图所示，处于平行双导线中的电磁波信号被束缚于导线周边，仅可以沿着平行导线的走向进行长距离传输，就如同火车被束缚于铁轨之上一样。

高铁被束缚于铁轨

当平行传输线逐渐劈叉，本来束缚于其间的电磁波就“兜不住”了，开始向自由空间辐射，其过程如下图所示。（图片摘自公众号“无线深海”）

偶极子天线辐射机理

---

二、分析理论

天线分析理论包括2方面内容：1）：电磁场的基本原理；2）电磁波辐射基本理论。

• 电磁场的基本原理

电磁场的基本原理主要涉及天线分析的相关基本理论：

1）maxwell方程组；2）格林函数与叠加原理；3）互易原理；4）惠更斯原理；5）对偶原理；6）巴比涅原理；7）镜像原理；8）缩比原理。

• 电磁波辐射基本理论

电磁波辐射理论主要介绍四种基本辐射模型：

1）基本电振子辐射；2）基本磁振子辐射；3）基本缝隙辐射；4）基本面元辐射。

这四种基本辐射模型是形式多样、结构迥异的天线辐射分析的基础。 理论介绍的重点是基本电振子辐射分析过程，后续三种基本模型的分析过程与基本电振子均有着千丝万缕的联系。

基本分析理论

1. 电磁波的基本原理

• Maxwell方程

1758年，库仑通过实验得出了“库仑定律”，其最直观的物理现象规律就是“电荷的同性相斥，异性相吸”，同时也给出了“排斥力”或“吸引力”与电荷量大小之间的定量关系，从而引出了“电场”概念，即 一个电荷对另一个电荷的力作用是通过该电荷在周围空间产生的“电场”来实现，电荷量越大，产生的电场就越强 ，对另一个电荷的作用就越强烈，这其实和“气场”是一样一样的，强大的人会在周围产生强大的气场，从而影响周围的人，能力越强，气场越强。

1820年，奥斯特发现了 电流的磁效应，即 运动的电荷(电流)可以在其周遭的空间产生磁场 ，其后数月，毕奥和萨伐尔以及安培给出了磁场与电流的定量关系，即毕奥-萨伐尔公式和“安培环路定理”。

1831年，法拉第通过实验发现了“磁生电”现象，即电磁感应定律： 变化的磁场可以产生电流 ，其后天才物理学家麦克斯韦引入了 “位移电流” 的概念，说明变化的电场也可以产生磁场，即“电生磁”。

至此，电与磁的关系基本明朗：电荷产生电场，电荷的移动（电流）引起电场的变化，变化的电场又会产生磁场，变化的磁场又会产生电场……，如此循环往复， 电场与磁场的互相激发，从而以电磁波的形式向无穷远处传播 。

麦克斯韦在总结前人试验结果的基础上，凭借着他坚实的数学功底， 定量的统一了“电”与“磁” ，这就是被誉为最伟大的物理公式——Maxwell方程，它的诞生为后续整个电磁大厦的建设奠定了最为重要的基础，作为微波器件之一的天线，其辐射特性的分析的全部理论自然基于此展开。

• 格林函数与叠加原理

如图所示，格林函数是点源在空间产生的电磁场分布（即波动方程的解）。当点源的场（即格林函数）已知，则任意源分布的解可以由叠加原理获得。

我们可以用LED小灯泡光场分布来进行类比，一个小灯泡在空间中产生光强可以表示为格林函数，那N个小灯泡组成的LED阵，在空间产生的光强就可以表示为每个小灯泡产生的光强进行叠加。

一盏小灯泡

N盏小灯泡

• 互易原理

电磁场的互易定理是关于两组源的定理。在一定的介质条件下，两组源的互易关系成立：1） 天线A受到一给定激励后在天线B终端获得的电流，等于天线B受到同一激励时在天线A终端获得的电流 ；2）同一天线用作 辐射时的辐射特性 ，包括远场方向图，天线实效长度和天线输入阻抗等，同于该天线用于 接收时的接收特性 。

互易定理在实际工程中广泛应用，比如天线测试中，很多实际工程中作发射用的天线，实际测试中却不方便继续测试其发射电磁波，此时，可以将其作为接收天线，测量其辐射特性，依据互易定理，测试结果是相同的。

天线测试

需要说明的是，互易定理的成立对于介质特性有一定要求，对于不满足要求的材料（铁氧体材料或等离子体材料），互易定理不成立。****（具体见《天线工程手册》）

• 惠更斯等效原理

惠更斯等效原理表明，如果闭合体的表面S上的场已知，则S以外的场可由S面上的场进行计算，即：S内真实源在S面外产生的电磁场分布可以用S面上的等效源等效产生。即如下两个图的在虚线外产生的电磁场分布“E”和“H”是一致的。等效原理可以帮助我们更为简单的分析诸如喇叭天线，抛物面天线等形式的面天线。

等效原理

• 对偶原理

麦克斯韦方程组中，只要引入磁荷密度和磁流密度 , 则上文中经典的麦克斯韦方程则转化为具有完全对称性的广义形式，相应的场也具有类似的电磁对应关系。

对偶关系

依据“电”与“磁”的对称关系，碰到任何电磁关系式，将等式中的虚线上方的电磁参量全部替换为虚线下方的参量，等式依旧成立。

• 巴俾涅互补原理

巴俾涅互补原理描述了具有互补结构和对偶源的两电磁场问题的解之间的相互关系。在天线工程中，常利用巴俾涅互补原理从已知天线的辐射特性方便地导出其互补天线的辐射特性。在散射分析中，亦有类似的用途。

无限大导体电屏上的缝隙天线与互补的电振子天线的辐射特性互补，这种方法可以被用于分析缝隙天线的辐射特性。

• 镜像原理

在很多辐射－散射问题中，源的附近存在着电尺寸很大的金属板。这时，金属上方的辐射场可根据镜像原理求解。

在镜像原理中，当抽掉无限大理想导电（导磁）平面后，在下半空间不仅要有对应的镜像源，同时要有对应的镜像散射体。镜像散射体与原散射体位置、形状以无限大导电（导磁）平面为对称。

需要说明的是， 镜像原理仅对真实源存在的半空间的场分布是等效的，对于镜像源存在的半空间的场不等效 ，电流和磁流分别以垂直方式和水平方式放置于无限大PEC和PMC上时，其镜像源的特征如下图所示。

不同源的镜像

• 缩比原理

在分析电磁问题时， 我们时常关心目标的电尺寸（ ）而非物理尺寸 ，这主要因为缩比原理，它描述了具有不同物理尺寸但保持相同电尺寸的两个辐射－散射问题中场分布的相似性，这也正是室内使用缩比模型代替全尺寸模型进行RCS测试的理论依据。

缩比原理成立的条件是： 需要保持介质电特性参数（介电常数与磁导率）不随频率变化 。在实际的辐射－散射问题中，若在介质中电导率为0，金属结构中电导率趋于∞，则材料的介电常数可以视为不随频率变化，这时，缩比模型中辐射方向图、天线输入阻抗等都和真实尺度下的方向图和天线输入阻抗非常接近。利用场的缩比原理，可以在实验室内对大尺度辐射－散射问题的场分布进行较为准确的模拟研究。

但是， 当介质为有耗媒质，即电导率不为0，或天线馈线中金属导体的电导率不是∞，随着频率的变化，材料的介电常数也会相应的发生变化，这时缩比原理不成立 ，利用缩比原理测量导致的输入阻抗较之方向图误差也要大一些。

2. 电磁波辐射基本理论

天线分析理论构成

依据Maxwell方程求解空间电磁场分布的方法有两种，一种是 “直接法” ，另一种为**“间接法” 。所谓 “直接法” ，就是直接依据目标体上“电流”和“磁流”分布，计算空间电磁场的分布。而所谓的 “间接法”**，就是通过引入中间变量 磁失位“A” 和 电标位“ ”，来简化波动方程，完成中间变量的求解后，再通过电场“E”和磁场“H”与位函数的微分关系，完成电场和磁场分布的求解，其 基本思想就是将一个复杂的求解问题通过分步求解的方式来降低求解难度。 其具体实现为：

若场域中只存在电荷源和电流源，则有：

那么磁场B可以表示成为一个矢量的旋度，即为：

带入maxwell方程组，则有：

或

旋度为0，则可以定义一个标量电位的梯度代替上式括号中的复矢量，从而有：

至此，我们就建立电磁场“E”、“H”与中间变量“A”和“”的关系，利用该关系，可以将maxwell方程中的“E”和“H”全部替换掉，从而建立“A”和“”满足的波动方程：

可知，中间变量满足的波动方程的形式要比“E”和“H”满足的波动方程的形式简单很多，该方程的解可以借助“格林函数”快速求出：

求出中间变量的空间分布后，利用“E”、“H”与中间变量的关系，即可求解出空间中电磁场的分布。

• 基本****电振子的辐射

• 场的分布形式

基本电振子：又名电流元或电偶极子，指的是无限小的线性电流单元，即其长度l远小于工作波长。