

超级源随SSF稳定性补偿分析(一)
描述
先来名词解释,SSF:Super Source Follower,也就是大家常说的超级源随。
SSF稳定性补偿这个话题分两篇文章介绍。 第一篇文章分析常见SSF结构的稳定性和频率特性,结论肯定是不好。 第二篇文章介绍一种SSF稳定性补偿方案。
SSF应用场景:
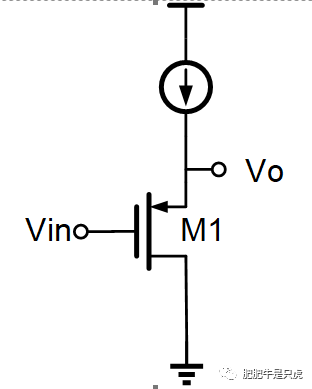
上图为普通源随,其DC输出阻抗为1/gm1,通常是是一个相对的低阻点。
在诸如部分LDO应用中(见下图),我们需要一个理想Buffer来隔离输出传输管Gate端的大寄生电容,我们期望Buffer输出阻抗足够低,从而使得N2处的极点处于高频处(带宽之外),以改善系统稳定性。
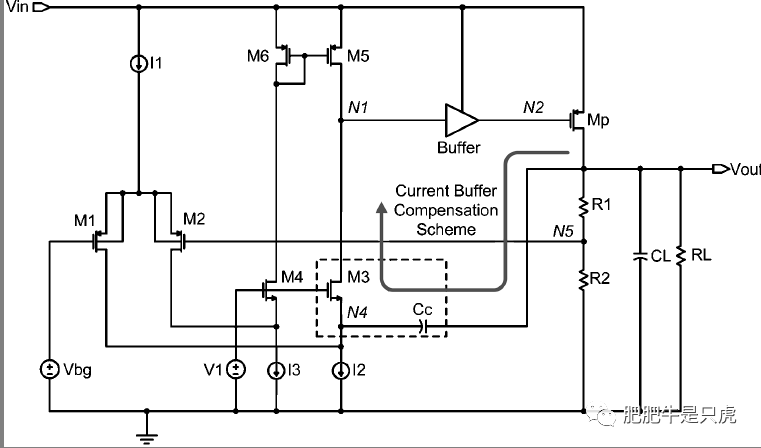
普通源随的输出阻抗1/gm1的值与偏置电流相关,为了得到比较低的阻抗,需要较大的偏置电流和较大的MOS尺寸。 另一方面,较大的MOS尺寸又会带来较大的寄生电容,进而影响带宽。
SSF可以在不显著增大偏置电流的情况下,通过引入一个local feedback环路,大大降低源随的输出阻抗。
SSF常见结构的稳定性分析:
SSF常见结构见下图,这里需要说明的是,R1可以是一个电阻,也可以是一个电流源的等效内阻。
说明:在小信号分析过程中,忽略MOS的沟道电阻(足够大)
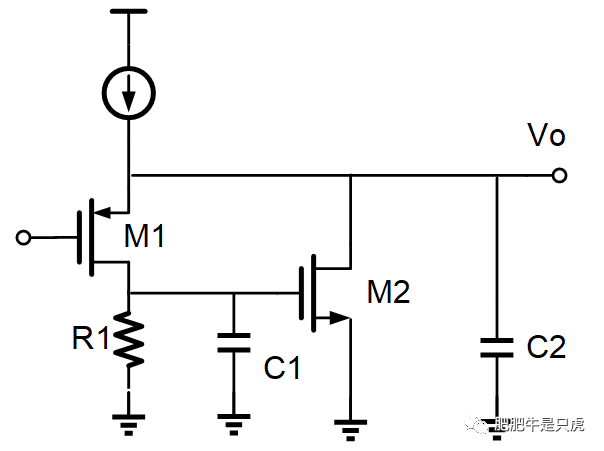
1:等效Gm(s)的推导
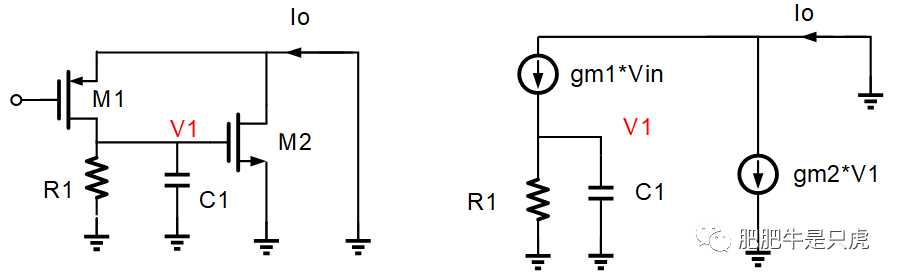
推导过程省略,直接写结果:
Gm(s)=gm1+gm1GM2R1/(1+秒)R1C1)
2:等效输出阻抗Zout(s)的推导
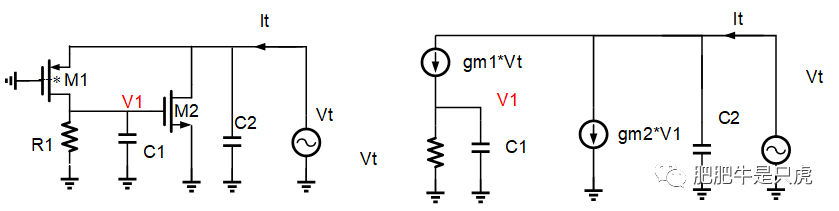
推导过程省略,直接写结果,写成导纳的形式:
痛风=gm1+gm1GM2R1/(1+秒)R1C1)+s*C2
3:闭环增益的推导:
联合上面Gm(s)和gout(s)的表达式,可以得到闭环增益的表达式

4:闭环稳定性分析:

很显然,上述推导出来的结论并不能保证p1<
令闭环增益分母as^2+bs+c=0 , 可以得到两个解(也就是2个极点),初中数学我们知道,当b^2-4ac>0时,两个根为实根,系统为过阻尼系统,根据此条件得到以下结论:C1>4C2*gm2/gm1
为了维持系统的稳定性,C1的取值居然比C2要大很多,此时,闭环系统近似为一个单极点系统,其闭环带宽为gm1/C2,和常规Source Follower一样,所以这个补偿方案很不合理。 我们需要寻求更加合理的稳定性补偿方案,这就是接下来下篇文章的工作。
-
 jf_32520285
2024-08-30
0 回复 举报重极点位置与零点位置接近吧,为什么还需要补偿呢 收起回复
jf_32520285
2024-08-30
0 回复 举报重极点位置与零点位置接近吧,为什么还需要补偿呢 收起回复
-
 jf_87862142
2024-06-29
0 回复 举报是开环增益吧 1条回复 收起回复
jf_87862142
2024-06-29
0 回复 举报是开环增益吧 1条回复 收起回复 -
 CDongJ
0
这个ss结构本身就是一个反馈系统
CDongJ
0
这个ss结构本身就是一个反馈系统
-
电压跟随器的稳定性分析2025-02-17 1642
-
电阻器的热稳定性分析2024-12-04 1422
-
如何对基于MOSFET的VI电流源进行稳定性仿真?2024-07-31 559
-
运放稳定性的判断原理的补偿原理?2024-05-06 1915
-
怎么分析电路的稳定性?2023-09-17 3315
-
超级源随SSF稳定性补偿分析(二)2023-05-23 7010
-
AN-593:ADP3178密勒补偿式线性调节器的稳定性分析与暂态分析2021-04-24 827
-
开关电源环路稳定性分析2020-05-31 3916
-
开关电源增益稳定性分析2018-10-22 2126
-
LDO稳定性分析2011-11-01 861
-
影响电力系统电压稳定性的因素分析2010-10-14 901
-
电感的稳定性2009-08-22 1818
-
电阻的稳定性2009-06-15 2456
-
高稳定性参考电压源电路图2009-04-14 1130
全部0条评论

快来发表一下你的评论吧 !

