超级源随SSF稳定性补偿分析(二)

update内容：

（1）Gm(s)小信号图中M1的小信号电流方向反了，虽然不影响计算结果，还是更正过来；

（2）增加“模型仿真验证”这部分内容，通过建模仿真验证推导的相关结论

本文介绍一种SSF稳定性补偿方案，并推导其闭环特性，给出相关参数的设计指引。

基本结构：

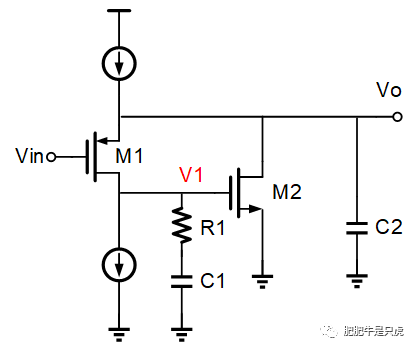
在节点V1引入一个RC串联支路，从直观上来看会引入一个零点-1/(R1*C1)，用于抵消环路中的某个极点。

Gm(s)的推导：

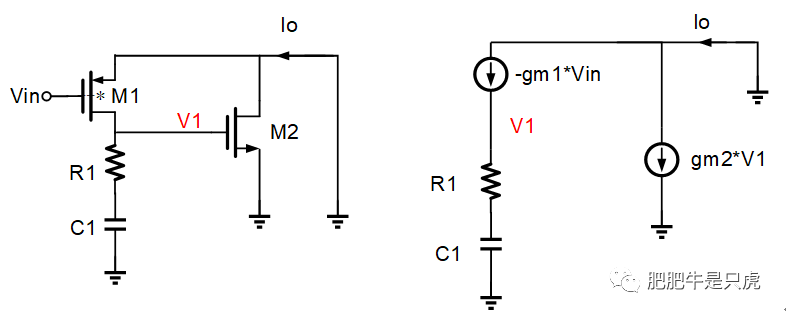
对照小信号图，可以直接写出结果：

Gm（s）=gm1+gm1GM2（R1+1/（sC1））

zout(s)的推导：

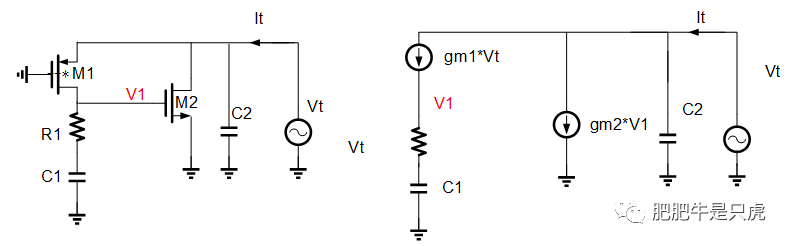
对照小信号图，可以直接写出结果，这里还是用导纳吧，后面的推导似乎更简洁一点：

痛风=gm1+gm1GM2（R1+1/（sC1））+sC2

闭环增益A(s)的推导：

联合上面Gm(s)和gout(s)的表达式，可以得到闭环增益：

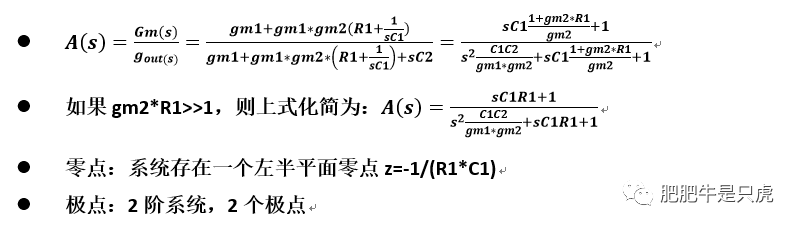
闭环稳定性分析：

零点和主极点抵消，整个系统近似为一个单极点系统，闭环带宽为gm1/C2A2，其中A2=gm2R1。 这个带宽明显比常规Source Follower的带宽gm1/C2要大得多。

通过引入Local Feedback，我们成功地将带宽从gm1/C2扩展A2倍，为了得到更好的效果，A2=gm2*R1要足够大。

接下来关于R1和C1的取值问题，初中数学我们知道，要想闭环系统两个极点都是实根，必须满足时b^2-4ac>0，此时系统为过阻尼系统，可以得到以下结论：

C1>4C2/(A1A2)，其中A1=gm1R1，A2=gm2*R1, 相对于C2，C1是一个比较小的值

需要注意的是，我们在计算中忽略了V1节点的寄生电容Cp，C1在取值过程中需要保证C1>>Cp

小信号模型验证：

搭建小信号模型，通过仿真验证前面推导的相关结论，在次之前先把前面推导的基本结论先列举一下：

p2=-gm1/C2*A2；p1=z1=-1/(R1*C1)

以上零极点表达式成立的前提条件是A2=gm2*R1>>1，仿真过程中至少保证A2>10

闭环带宽: 理论上与C1取值无关，C1取值范围：C1>4C2/(A1A2)

仿真Bench见下图，各个参数的取值见上表

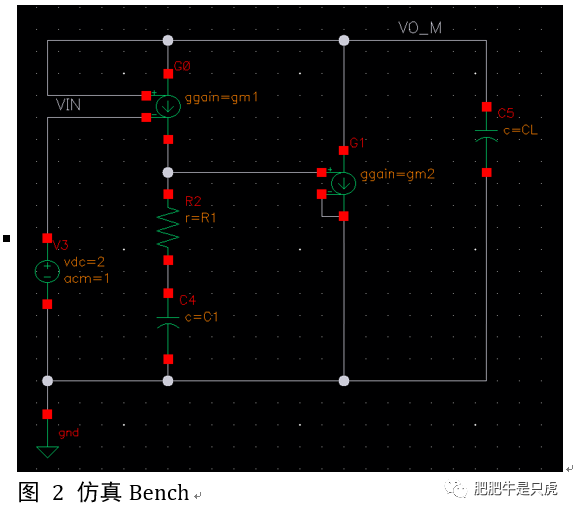
先通过仿真观测R1和闭环带宽之间的关系，从前面的推导可知，带宽=gm1/C2(gm2*R1)，R1和带宽成正比。

仿真结果见下图，仿真结果显示，闭环带宽完全和R1成正比，R1越大，闭环带宽越高。

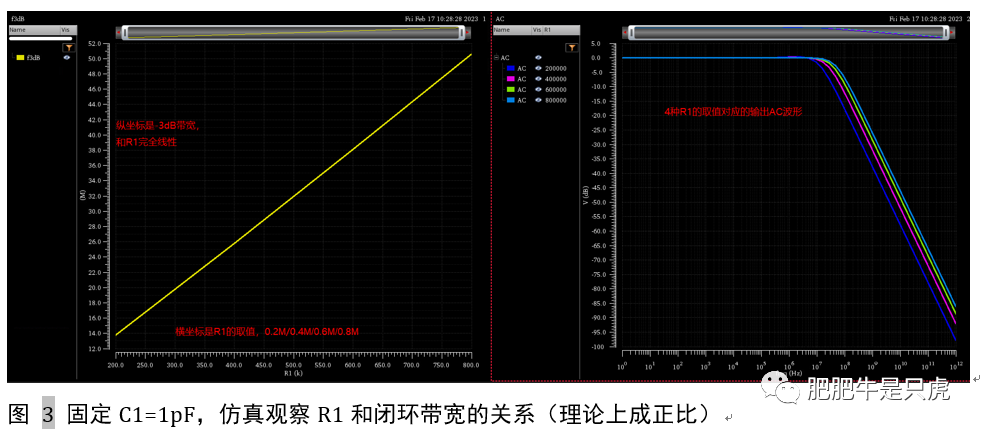
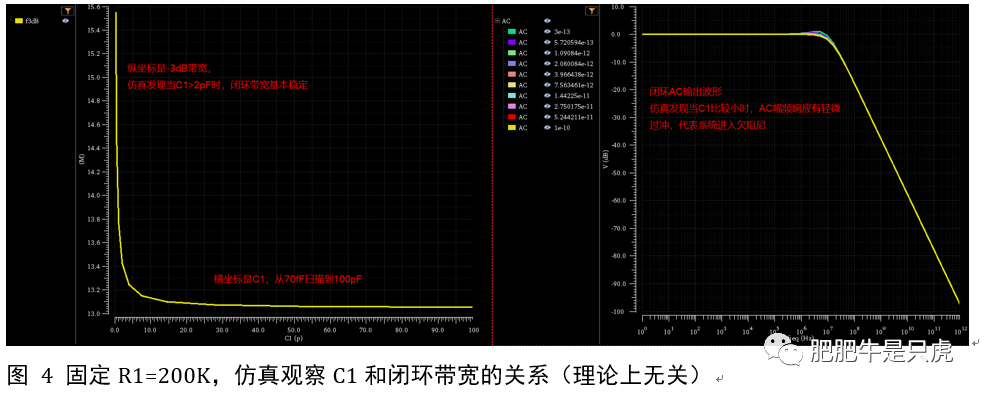
然后通过仿真观测C1和闭环带宽之间的关系，从前面的推导可知，带宽=gm1/C2(gm2R1)，C1理论上和带宽无关，但是需要注意的是，需要满足约束条件C1>4C2/(A1*A2)。

仿真结果见下图，仿真结果显示，只要C1足够大（>2pF），闭环带宽与C1无关的结论是成立的。但是也应该注意到，系统临界阻尼状态对应的C1和理论计算还是有所出入，造成这个计算误差的原因应该是在计算关系式b^2-4ac>0时，系数b和a做了A2>>1的近似。在设计的时候可以将C1适当取大一点，pF级。However，这个其实不太重要，系统即便是进入轻微欠阻尼状态，也不是什么大问题。

除了小信号模型，我还用真实电路进行了验证，结果都很相近。

总结：

我们推导了SSF补偿方案，给出了设计指引，并建模通过仿真对相关结论进行了确认。

RC串联支路补偿方案有效

R的取值和闭环带宽成正比，带宽越高，LDO 传输门Gate端极点频率越高

C的取值和闭环带宽无关，仅仅需要满足一定的约束条件，取值范围非常大