

正反馈系统稳定性分析
描述
我们常见的环路大部分都是负反馈环路,对于负反馈系统的稳定性,我们有相应的稳定性判据。
如果环路是正反馈系统,系统是否一定不稳定?
最常见的Widlar电流源电路其实就是一个正反馈系统。
正反馈系统模型
下图为一个正反馈系统,开环系统是一个单极点系统,其开环传函为:
Ao(s) = Ao/(1+s/p1),极点=-p1,为LHP极点。
输出Vo作为反馈信号和输入信号Vin叠加,形成一个正反馈系统
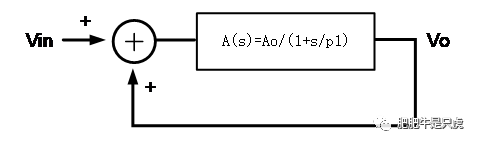
我们尝试推导闭环传函,Ac =Ao(s)/(1+Ao(s)),将Ao(s)的传函代入可得闭环传函为:
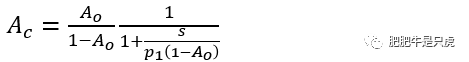
观察上述闭环传函,,有以下结论:
1.闭环DC增益:Ao/(1-Ao)
2.闭环极点:-p1(1-Ao)
正反馈系统稳定性分析
对于一个闭环系统,我们可以根据其极点位置来判断其稳定性:如果其极点位于LHP,则系统稳定;如果其闭环极点位于RHP,则系统不稳定。
回到这个正反馈系统,其闭环极点=-p1(1-Ao),这个正反馈系统的稳定性分为2种情况:
如果Ao>1,闭环极点>0,为RHP极点,系统不稳定
如果Ao<1,闭环极点<0,为LHP极点,系统稳定
Matlab验证正反馈系统稳定性
借助matlab,用阶跃响应验证正反馈系统的稳定性,代码如下:

先考虑Ao<1的情况,根据前面的推导,此时正反馈是稳定系统。令Ao=0.5,其阶跃响应见下图,很明显阶跃响应是收敛的,系统稳定。
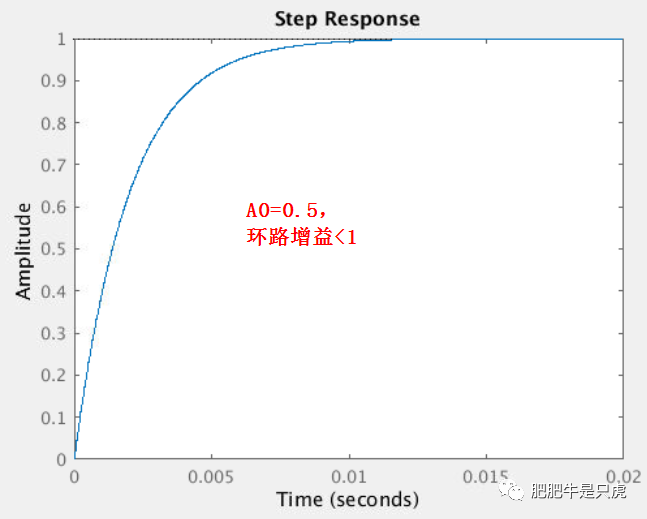
再来验证Ao>1的情况,根据前面的推导,此时正反馈是不稳定系统。令Ao=1.1,其阶跃响应见下图,很明显阶跃响应是发散的,系统不稳定。
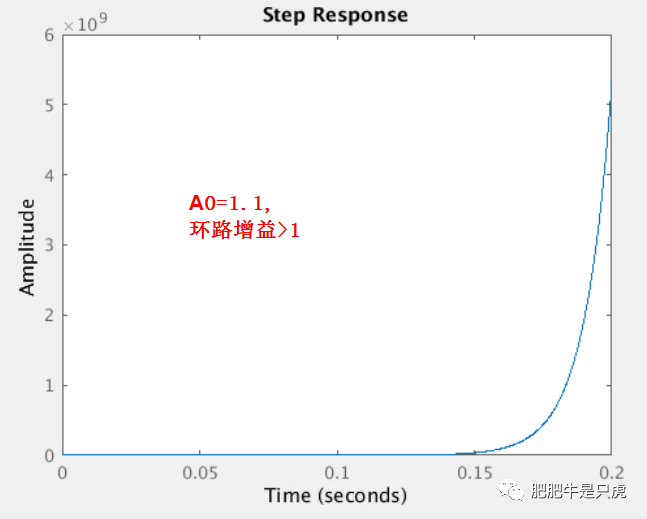
声明:本文内容及配图由入驻作者撰写或者入驻合作网站授权转载。文章观点仅代表作者本人,不代表电子发烧友网立场。文章及其配图仅供工程师学习之用,如有内容侵权或者其他违规问题,请联系本站处理。
举报投诉
-
正反馈调节与负反馈调节的区别2025-01-18 9332
-
buck电路的稳定性分析方法2024-11-21 2524
-
电压反馈运算放大器的稳定性分析2024-10-29 409
-
运放正反馈是不是比负反馈更加容易振荡啊?为什么啊?2024-09-05 859
-
TINA可以进行运放的稳定性分析吗?2024-09-04 285
-
模电中正反馈和负反馈的区别2024-07-30 5365
-
关于电源/负载电路组合的稳定性分析2021-05-11 2336
-
开关电源环路稳定性分析2020-05-31 3925
-
线性定常系统的瞬态响应和稳定性分析2016-09-01 1858
-
运放稳定性分析2016-02-19 973
-
LDO稳定性分析2011-11-01 862
-
基于电压电流反馈的调速系统稳定性分析2010-08-03 779
-
频率响应法-相对稳定性分析2009-07-27 3440
全部0条评论

快来发表一下你的评论吧 !

