

聚类分析中的机器学习与统计方法综述(二)
描述
在本节中,我们将阐述八种应用在单细胞转录组数据的聚类方法,并总结了这些方法的优点、局限性和时间复杂度等。一部分单细胞聚类的工具会使用多种聚类算法,因此会在多个类别中列出。
01
基于划分的聚类
基于划分的聚类方法主要是确定最佳的K个中心,将数据点划分为K个簇,其中心要么是质心(均值),称为k-means,要么是中心点,称为k-medoids。 k-means方法的思想是找到质心,以最小化每个数据点与其最近质心之间的欧氏距离的平方和。它具有时间复杂度低的优点。但是,它对异常值很敏感,并且用户必须预先指定聚类的数量K。对于将N个D维数据点聚为K个类,使用Lloyd 's算法的k-means每次迭代的时间复杂度为O(KND)。 以下是一些使用k-means聚类的单细胞转录组数据分析工具。SAIC在迭代聚类过程中使用k-means并结合ANOVA识别特征基因;SCUBA使用k-means将每个时间点的细胞分为两组,并使用间隔统计量来识别分叉事件;SC3的步骤之一是在细胞距离矩阵上使用k-means聚类(图3)。k-medoids方法是将原始N个数据点中的K个数据点识别为中心点,以最小化数据点到中心点的距离之和。它非常适用于以有意义的中心点作为聚类中心的离散数据。然而,与k-means类似,它对异常值很敏感,用户必须预先指定聚类的数量K。对于从N个数据点中选择最优K个点的组合问题,采用围绕中心点划分算法的k-medoids的时间复杂度为O(K(N−K)2)。
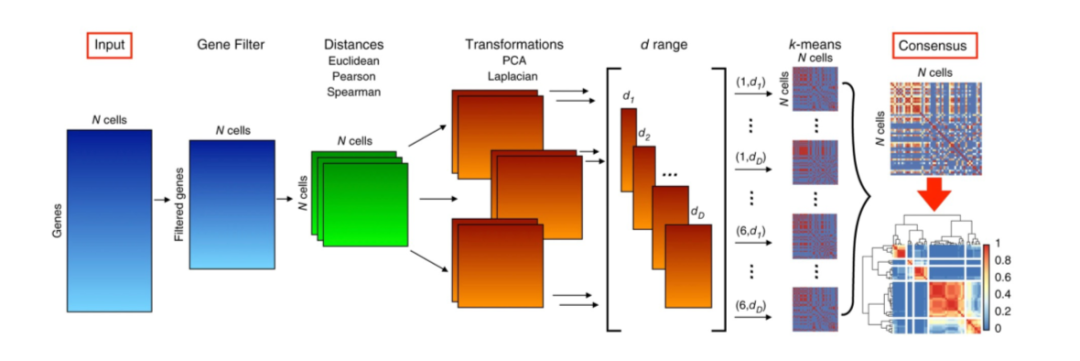
Figure 3. SC3聚类流程图
RaceID2用于利用单细胞转录组数据识别罕见细胞类型,结果表明用k-medoids取代k-means方法进行聚类可以明显改善聚类的结果。
02
层次聚类
次聚类是基因表达数据分析中应用最广泛的聚类方法。层次聚类在数据点之间构建层次结构,它根据层次树中的分支定义不同的类群。许多单细胞转录组数据的聚类算法都是基于层次聚类或将层次聚类作为分析的步骤之一。
层次聚类对数据本身的分布并没有过多要求,因此,它适用于许多不同形状的数据集;层次聚类的另一个优点是通过数据点之间的层次关系,可以用于发现其内在的关联,有助于对结果的解释。层次聚类主要有两种实现方法:聚合式(agglomerative)和分裂式(divisive)。 聚合式又叫“自下而上式(bottom-up)”的聚类,它从N个数据点开始,每一个数据点作为一个单独的类,在每一步中,类群依据它们之间的距离进行合并,直到所有类群在层次结构的根处合并在一起。分裂式又叫“自上而下式(top-down)”聚类,相比之下,该方法首先将所有数据点当成一个类群,然后每一步递归划分更小的类群,直到分成N个类群为止。无论是哪一种,层次聚类的一个显著缺点是时间复杂度高,运行时间非常久。此外,层次关系并不能提供数据点的最佳聚类划分,还需要一个额外的步骤来从层次树中决定最终划分的类群数量。 BackSPIN是一种双聚类算法,分别在细胞和基因的维度上应用层次聚类。BackSPIN使用SPIN迭代地拆分基因表达矩阵,直到在分支处不再满足拆分标准;cellTree通过在话题分布上构造最小生成树,从而在单个细胞之间构建层次结构;CIDR对PCoA获得的低维嵌入使用了层次聚类;ICGS采用层次聚类,将筛选后得到的一组基因的表达数据按表达水平和动态范围进行聚类,并进行配对相关分析;SC3对多个k-means聚类结果合并得到的一致性矩阵进行层次聚类;为了获得层次结构中的实际类群,DendroSplit通过衡量与原始表达数据的分离分数,使用动态拆分和合并分支来检测层次树中的类群。
03
混合模型
混合模型聚类基于的假设思想是,数据点是从几个混合的概率分布中采样,每个概率分布代表一个聚类。样本的聚类是通过从每个分布中学习其生成的概率来推断的。用于聚类的常见混合模型主要包括应用于连续型数据的高斯混合模型(GMM)和计数型数据的分类混合模型。
混合模型的优点包括严格的概率建模和在模型中引入先验知识的灵活性。然而,解决混合模型需要先进的优化或采样技术,具有较高的计算复杂度,并依赖于关于数据分布的假设的准确性。混合模型通常是用期望最大算法学习的,它可以推断混合参数和类分配似然性,也可以用抽样和变分方法学习图概率模型。此外,混合模型的时间复杂度取决于混合的分布,比如在GMM中,时间复杂度为O(N2K)。 BISCUIT基于层次狄利克雷过程混合模型(HDMM),并附加细胞特定的标准化和dropouts矫正。它的过程首先是应用HDMM对细胞建模,形成包含Dirichlet先验的混合系数、均值、Wishart先验的协方差矩阵的高斯混合模型,而细胞特定的缩放因子代表了技术变异。早先版本的Seurat能够将单细胞转录组数据与原位RNA测序相结合,用于单细胞的空间聚类。在双峰混合模型中,针对一组选定的标志基因,将单细胞转录组数据与二值化的原位RNA数据整合,然后通过双峰混合模型中单细胞转录组表达谱的后验概率将每个单细胞分配到不同的空间类群区域。
04
基于图的聚类
在基于图的聚类中,数据点被表示为图(Graph)中的节点,而节点间的边(Edge)由数据点之间的相似性表示。基于图的聚类基于一个简单的假设,即图中的密集社区(community)表示为密集的子图或谱成分,因此对于数据的分布并没有过于依赖。两种最常用的图聚类算法是谱聚类和团(clique)发现。
在谱聚类中,通过相似函数(如RBF核函数)建立相似性矩阵及其拉普拉斯图。通过计算拉普拉斯图的顶部特征向量,以便后续的k-means聚类。虽然可以使用更有效的方法来寻找固定数量的顶部特征向量,但寻找所有特征向量的时间复杂度为O(N3),因此,谱聚类并不适用于大数据集。当细胞类型作为先验已知时,基于TCC的聚类利用细胞间的Jensen-Shannon距离构建相似性矩阵进行谱聚类;未知时则应用近邻传播聚类。 在图论中,团被定义为每对节点都相邻的子图,因此,团代表了图中数据点的类群。由于在图中找到团是一个NP-hard问题,通常会使用启发式方法。SNN-Cliq利用单细胞转录组数据对细胞进行团簇检测。在稀疏图中团通常很少见,因此,SNN-cliq在SNN图中检测到的团一般是密集但是不完全连通的。
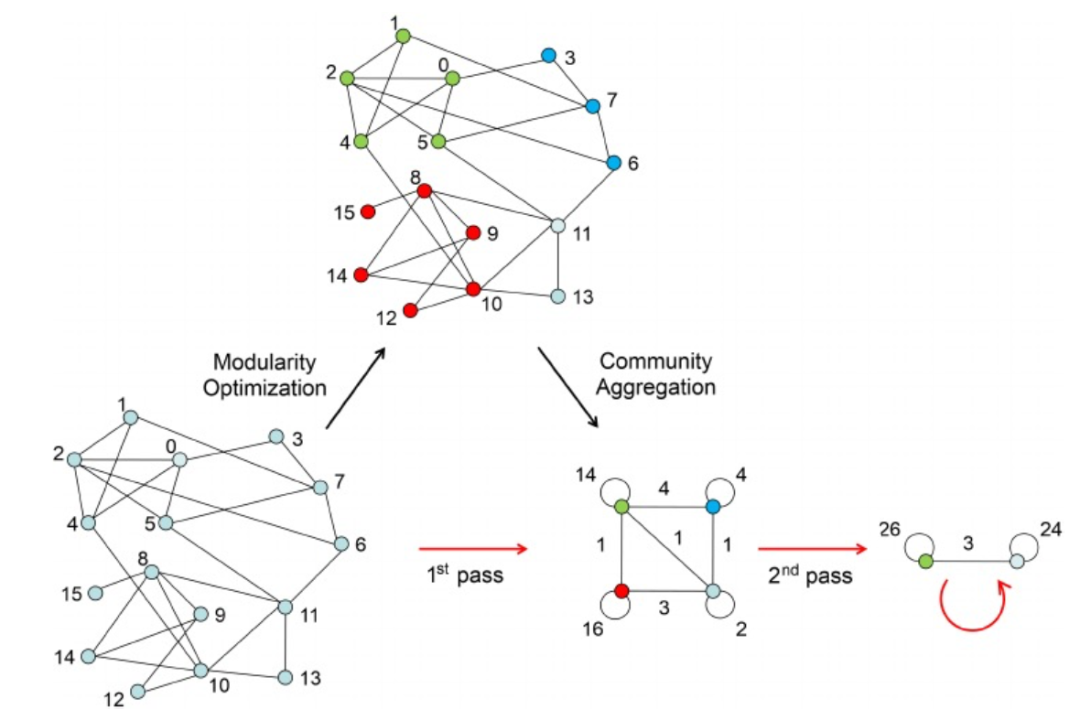
Figure 4. Louvain算法示意图
另一种常用于单细胞分析的基于图聚类的算法是Louvain算法(图4)。Louvain是一种社区检测算法,它比其他基于图的算法更具可扩展性,通过贪婪方式将节点分配给社区,并更新网络以获得低分辨率的聚类。Louvain的时间复杂度为O(NlogN)。Scanpy是一个集成了Louvain算法、提供了一个能够分析大规模单细胞转录组数据集的工具。Seurat在默认情况下也是利用Louvain算法在细胞SNN图上来发现细胞类型。
05
基于密度的聚类
基于密度的聚类将类群定义为一个空间中具有高密度数据点的区域。DBSCAN和密度峰值聚类是基于密度的聚类的两个例子。
给定一个数据点,将其作为中心以ε为半径划分出一个球形,球形内的数据点数量如果超过指定的阈值,那么这些数据点就被DBSCAN认为是一个类群。对每个数据点重复该过程,不断扩展,最终完成聚类。该方法具有效率高、适用于任何形状的数据的优点。然而,密度聚类对参数非常敏感,如果类群密度不平衡,结果会非常差。DBSCAN聚类的时间复杂度为O(NlogN)。基于密度的聚类通常用于单细胞转录组数据分析中的异常细胞识别,如GiniClust和Monocle2。 GiniClust是基于DBSCAN来发现罕见的细胞亚群,它使用基尼指数作为基因表达值变异性的衡量标准,以筛选高变基因,然后由DBSCAN对细胞聚类。密度峰值聚类考虑数据点之间的距离,而不是像DBSCAN那样考虑密度阈值,同时假设聚类的中心是聚类中数据点密度的局部最大值。密度峰值聚类的时间复杂度为O(N2)。在Monocle2中,就是对t-SNE空间内的细胞进行密度峰值聚类。
06
神经网络
Kohonen神经网络,也称为自组织特征映射神经网络(SOMs),运用竞争学习策略逐步优化网络进行聚类,使用随机梯度下降通过不断迭代训练数据点和每个中心的相似度来更新聚类中心。类群中心使用预定义的结构(如网格)进行初始化。SOM具有相当强的可扩展性,因为随机梯度下降不需要把所有的数据点保存在计算机内存中。此外,中心之间的预定义结构可以引入先验知识,并在类群之间提供可解释的关系。然而,SOM对参数异常敏感,比如用于更新权重的学习率。
SOM也已用于单细胞转录组数据的可视化和聚类。在一些研究中应用SOM在二维热图中直观的可视化相似关系。SCRAT为用户提供了可视化二维热图的选项,该热图反映了跨细胞群的基因之间的相关性。SOMSC利用SOM将高维基因表达数据折叠成二维,用于识别处于中间过渡状态的细胞以及拟时间排序。
07
集成聚类
集成聚类,也称为共识聚类,是一种广泛使用的策略。在该策略中,通过不同的应用场景(例如不同的聚类算法,相似的度量和特征选择/映射等)对同一数据集进行聚类,然后基于单个聚类结果之间的一致性,通过共识函数对它们进行合并。集成学习可以捕获不同数据或聚类模型中的多样性,并且已被证明比单一模型更健壮,并产生更好的结果。集成聚类的局限性是依赖于其他的数据转换和基本聚类方法。
SC3是一种用于单细胞转录组数据聚类的共识聚类方法。SC3首先通过三种不同的度量(斯皮尔曼、皮尔森和欧氏距离)来计算细胞间相似性,然后使用PCA和拉普拉斯转换进行分解,通过k-means对不同类型的低维嵌入进行聚类,接着用CSPA共识函数构建一致性矩阵,最后,利用该矩阵进行层次聚类。conCluster是另一种共识聚类方法,它使用多个不同的参数通过t-SNE和k-means进行了组合,然后将这些不同的组合连接起来,用于最后的k-means聚类。
08
近邻传播聚类
该聚类方法的主要思想是通过不同点之间的信息传递来选择聚类中心:吸引度(responsibility)用于描述一个数据点k作为数据点i的聚类中心的适合程度;归属度(availability)则描述了数据点i选择数据点k作为聚类中心的适合程度。近邻传播聚类的主要优点是不需要知道类群的数量。缺点是时间复杂度较高,对异常值敏感。当细胞类型数量未知时,基于TCC的聚类以该方式进行细胞的聚类。在SIMLR中也选项可以选择对数据进行该方法的聚类。
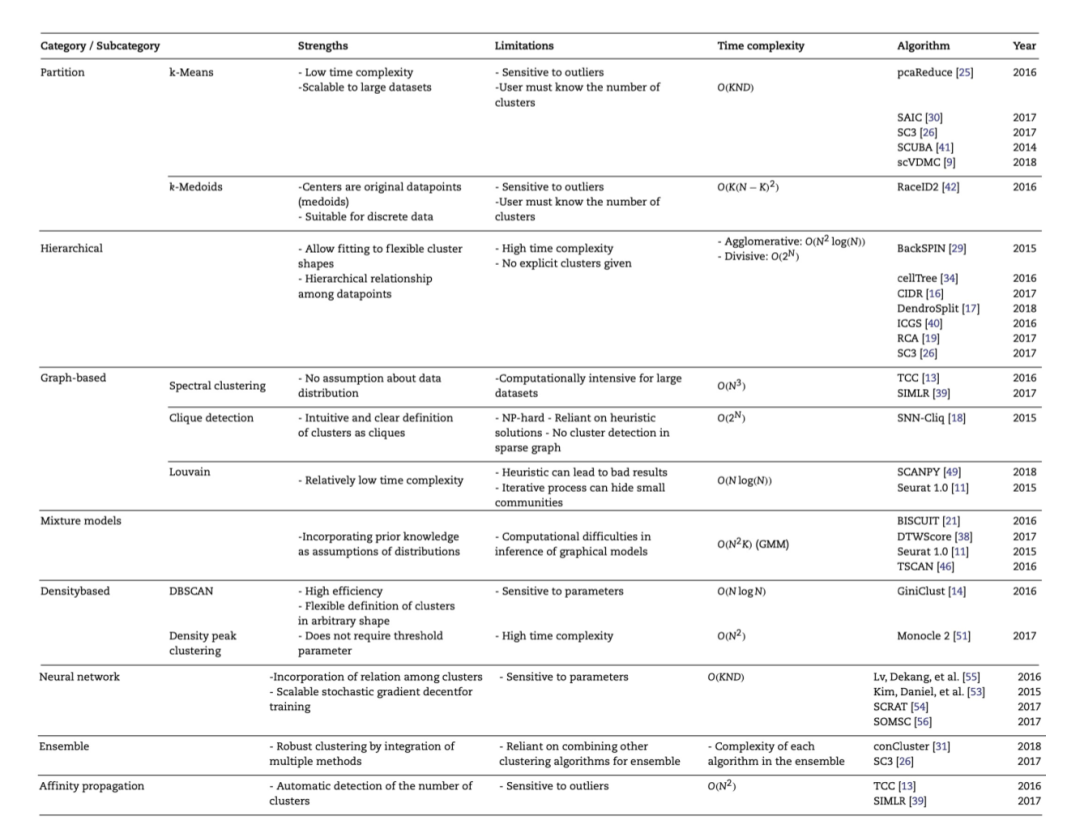
Table 1 聚类方法的分类及优缺点
审核编辑 :李倩
-
深度学习中的无监督学习方法综述2024-07-09 2690
-
聚类分析中的机器学习与统计方法综述(一)2023-05-19 1811
-
机器学习之分类分析与聚类分析2023-03-27 6582
-
机器学习之关联分析介绍2023-03-25 2646
-
水声被动定位中的机器学习方法研究进展综述2021-12-24 976
-
机器学习在卫星遥测分析建模中的应用综述2021-06-29 932
-
基于机器学习的哈希检索算法综述2021-06-10 829
-
基于Python的聚类分析及其应用简介2021-05-28 884
-
统计的学习方法2020-07-15 1721
-
Matlab提供的两种聚类分析2020-04-29 21629
-
机器学习入门宝典《统计学习方法》的介绍2018-11-25 5310
-
聚类分析方法有哪些2018-02-23 19082
-
基于主动学习的微博聚类分析2017-01-07 890
-
车联网建模和统计性质分析及其路由策略综述2016-03-24 719
全部0条评论

快来发表一下你的评论吧 !

