如何对spmv算法进行优化

主要是介绍如何对spmv算法进行优化。Spmv，即稀疏化的矩阵向量乘操作，关于稠密的矩阵向量乘操作，已经在上一篇文章中介绍过了。关于稀疏kernel的优化，是CUDA优化中最难的一部分，其难度在于稀疏特性千差万别，需要针对不同的应用、不同的数据选择不同的数据存储格式，然后再根据不同的数据特点进行特定的并行算法设计。而现实生活中，尤其是科学计算里面，基本上都是稀疏问题。在深度学习领域中，也一直有针对稀疏模型的研究，主要是针对推理方向，将模型进行剪枝之后，直接减少了计算量来达到对模型的加速目的。但实际上，为了保证模型的精度，稀疏度有限，且稀疏问题很难充分地利用硬件性能，导致了这一条路线其实并不好走。唠唠叨叨说了挺多，总之，稀疏kernel的优化是一个非常难的话题。本文会详细地介绍一下spmv。

一、前言

在说spmv之前，说一下稀疏格式。当矩阵中的绝大多数元素都是0时，需要一些特殊的格式来存储非零元素。这些格式也就是稀疏格式，常用的稀疏格式有：COO、CSR、DIA、ELL、HYB。深度学习领域还有blocked CSR、blocked ELL等。具体的稀疏格式总结见以下链接：

稀疏矩阵存储格式总结+存储效率对比:COO,CSR,DIA,ELL,HYB - Bin的专栏 - 博客园www.cnblogs.com/xbinworld/p/4273506.html

在本文中，使用CSR格式存储稀疏矩阵，后续所说的一系列优化也是针对CSR格式而言。说完了稀疏格式，现在再来说一下spmv，即稀疏矩阵向量乘。稠密的矩阵向量乘，即gemv已经在之前说过了。具体的操作即给定稀疏矩阵A和向量x，需要计算两者的乘积y。示意图如下。

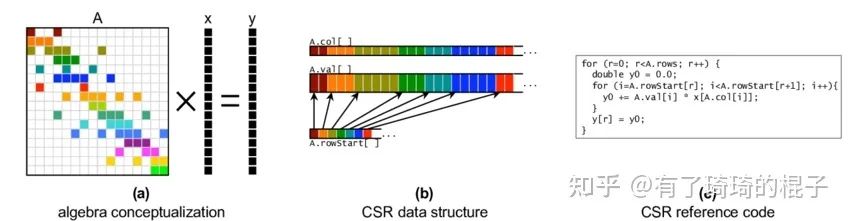
spmv介绍

二、并行算法设计

并行算法设计，主要是block和thread的设计，在这里主要参考了cusp的实现。有一个很重要的考虑是workload的分配。我们需要使用多少个线程来负责A矩阵中一行的计算？需要说明的是，在不同的数据特性下，需要采用不同的取值。如果这一行的元素非常多，那使用一个warp或者一个block，如果这一行只有一个元素，只需要一次乘加指令，那显然只能使用一个线程，毕竟用两个线程处理一个元素，怎么都不像正常人能干出的事。因而，我们假定一个参数，即THREADS_PER_VECTOR，来代表这个值。每THREADS_PER_VECTOR个线程为一组，他们需要负责A矩阵中一行元素的计算。

说完了这个核心思路，接下来看看每个线程需要干的工作。每个线程都要单独地对A矩阵的offset和index等进行读取，然后计算当前行的结果。如果每一行的元素特别少，比如这一行元素有4个，THREADS_PER_VECTOR就设为4，有8个元素就设为8，平均多少个元素，THREADS_PER_VECTOR就设为几，但上限是32。元素比32多的话，就多进行几个迭代即可。总之最多使用一个warp来处理一行元素。

至于如何得到一行元素有多少，row_offset数组长度除以y数组长度即可得。有必要在这里再提一句的是，这些参数的选择，以及对于不均衡的A矩阵元素如何处理，这些都是比较棘手的问题。有一大堆的论文在谈负载均衡和自动调参这两个事情，大家可以搜一下相关的论文瞅瞅。

讲完了思路，下面说一下具体的代码，如下：

 

template 
__device__ __forceinline__ float warpReduceSum(float sum) {
    if (WarpSize >= 32)sum += __shfl_down_sync(0xffffffff, sum, 16); // 0-16, 1-17, 2-18, etc.
    if (WarpSize >= 16)sum += __shfl_down_sync(0xffffffff, sum, 8);// 0-8, 1-9, 2-10, etc.
    if (WarpSize >= 8)sum += __shfl_down_sync(0xffffffff, sum, 4);// 0-4, 1-5, 2-6, etc.
    if (WarpSize >= 4)sum += __shfl_down_sync(0xffffffff, sum, 2);// 0-2, 1-3, 4-6, 5-7, etc.
    if (WarpSize >= 2)sum += __shfl_down_sync(0xffffffff, sum, 1);// 0-1, 2-3, 4-5, etc.
    return sum;
}

template 
__global__ void My_spmv_csr_kernel(const IndexType row_num,
                       const IndexType * A_row_offset,
                       const IndexType * A_col_index,
                       const ValueType * A_value,
                       const ValueType * x,
                       ValueType * y)
{
    const IndexType THREADS_PER_BLOCK = VECTORS_PER_BLOCK * THREADS_PER_VECTOR;
    const IndexType thread_id   = THREADS_PER_BLOCK * blockIdx.x + threadIdx.x;    // global thread index
    const IndexType thread_lane = threadIdx.x & (THREADS_PER_VECTOR - 1);          // thread index within the vector
    const IndexType row_id   = thread_id   /  THREADS_PER_VECTOR;               // global vector index

    if(row_id < row_num){
        const IndexType row_start = A_row_offset[row_id];                  //same as: row_start = Ap[row];
        const IndexType row_end   = A_row_offset[row_id+1];

        // initialize local sum
        ValueType sum = 0;

        // accumulate local sums
        for(IndexType jj = row_start + thread_lane; jj < row_end; jj += THREADS_PER_VECTOR)
            sum += A_value[jj] * x[ A_col_index[jj] ];

        sum = warpReduceSum(sum);
        if (thread_lane == 0){
            y[row_id] = sum;
        }   
    }
}

 

首先说一下传入的几个模板参数，IndexType代表索引类型，一般用int，如果矩阵十分巨大，可以考虑long long，ValueType代表数值存储的格式，科学计算一般都双精度，深度学习一般用单精度，或者fp16。推理甚至有一些int8这样的需求。THREADS_PER_VECTOR这个参数已经在前面说过了，VECTORS_PER_BLOCK则是代表一个block中有多少vector。我们尽可能地保证一个block有256个线程，所以VECTORS_PER_BLOCK = 256 / THREADS_PER_VECTOR。看完了模板参数，再看函数输入参数，分别是A矩阵的行数，A矩阵的CSR表示，有3个数组，然后是向量x和向量y。

接下来到了具体的kernel逻辑，首先计算了四个参数，需要注意的是thread_lane和row_id参数，thread_lane代表当前元素是当前组里面的第几个元素，row_id代表当前元素负责A矩阵中第几行的计算。接下来的逻辑也比较明了，先计算当前行对应的索引值，即row_start和row_end。定义sum变量来存储该行的计算结果，而后进行多次迭代，将每个线程对应的sum取出来，最后将sum元素进行warp的reduce_sum操作。最后将元素写到y向量中。

三、优化技巧

在上一节中已经把代码说完了，接下来盘点一下具体的优化技巧，以及优化中需要考虑的方方面面。 

1、合理的block和thread调整。我一直觉得这个点是优化中最重要的一点。核心就是THREADS_PER_VECTOR需要根据实际的数据进行调整。这一点主要是考虑到如果使用更多的线程处理的话，只有THREADS_PER_VECTOR个线程在工作，其他的线程都被浪费了。

2、Shuffle指令减少访存的latency。在不使用shuffle指令的话，只能通过shared memory完成最后的求和操作。从shared memory中取数比寄存器之间直接访问要花费更多的latency。因而要尽可能地使用shuffle指令。

3、对于global memory的合并访存。对于稀疏问题，由于CSR格式中的col数组和val数组不能保证地址对齐，因而针对global memory的合并访存其实是有一定的困难。我们可以仔细地来进行分析。当A矩阵行数比较多的情况下，spmv主要的访存有3部分，分别是A_value，A_col_index和x。其中，对于A_value和A_col_index的访存是连续的，但是由于地址不能保证对齐，所以访存效率大概率不会太高。而对于x的访存本身就是不连续的，因而cache命中率会显然易见地低。如何解决这些问题呢？对于A_value和A_col_index的访存问题，尚可以尝试对其进行数据填充，强制其地址对齐。而对于x的非连续访存问题，如何提高访存效率，这个问题就非常困难了。

4、关于向量化指令的使用。之前在进行gemm和gemv优化中大量地使用了float4这样的向量化访存结构。如何将向量化带到spmv中，这也是一个非常困难的问题。最大的根源是因为每一行的元素不确定，并且本身A中每行的元素就比较少，根本没有那么多数据去喂到LDS128指令上。

5、关于负载均衡的思考。CUDA上的负载均衡问题可以从两个角度考虑，一个是block之间的负载均衡，另一个是block/warp内，不同线程之间的负载均衡。关于spmv的负载均衡问题，可以参考一下Speculative Segmented Sum for Sparse Matrix-Vector Multiplication on Heterogeneous Processors。

四、实验与总结

最后，我们来说一下实验环节。实验主要用来说明两个问题，第一个是THREADS_PER_VECTOR参数对性能的影响，第二个是与cusparse的对比，用以观察不同数据下的性能表现。

实验一，从佛罗里达矩阵库里面选了一个稀疏矩阵，shyy41。平均一行有4.2个元素。我们在不同的参数下进行了实验，其结果如下：

THREADS_PER_VECTOR	spmv kernel耗时(ns)
2	4093
4	3969
8	4066
16	4368
32	4976

这个结果和预期的差不多，因为平均一行元素个数是4.2，所以THREADS_PER_VECTOR参数取4或8会有更好的性能表现。

实验二，从佛罗里达矩阵库里面随机选取了一些矩阵，其稀疏特性如下，矩阵旁边有x-y-z标识。x和y代表矩阵的行数和列数，z代表矩阵中的非零元个数。

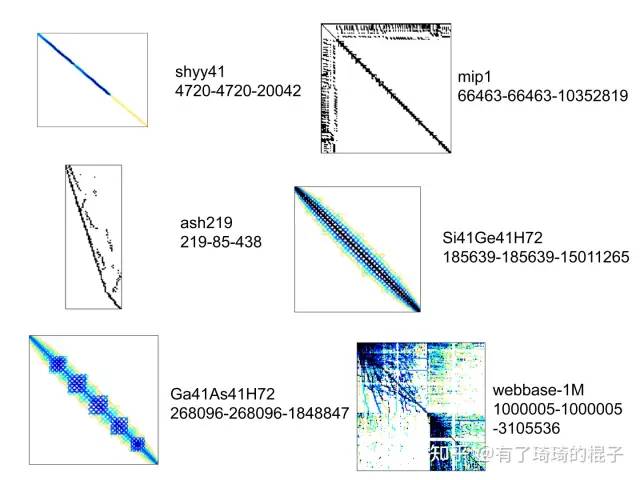
稀疏矩阵

性能表现如下，

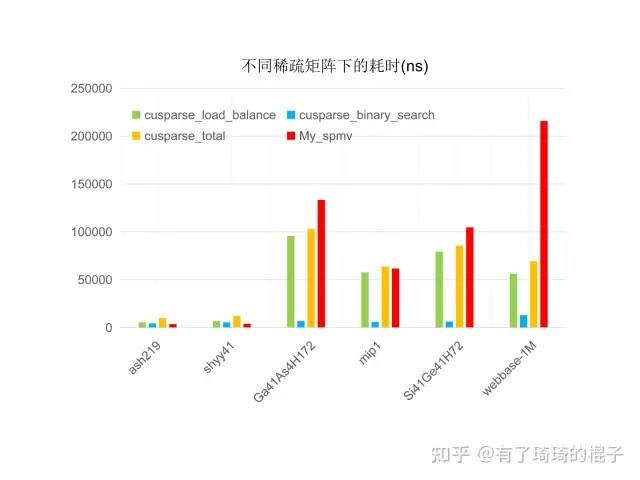
与cusparse的性能对比

结论：

1、先单独看cusparse的表现，库里面会调用两个kernel，分别是binary_seach和load_balance。这个名称简写了。总之，就是cusparse不管来的数据是啥，都会进行负载均衡，在数据量比较多的时候，额外的开销比较少，能够取到足够的效益。

2、如果是结构化的网格，即元素聚集在对角线附近，且每行的非零元都差不了太多的时候，我写的spmv会比cusparse快一些。如果每行的非零元方差特别大，cusparse中的负载均衡工作就发挥了威力，在web网络这种矩阵上能够比我的spmv快2-3倍。总之，在sparse问题中，负载均衡非常重要，我会在下一篇博文中说明如何在spmm中进行负载均衡。

总之，我们实现了spmv kernel，并对主要的优化技巧进行了解析和说明，然后大概地说了一下在spmv上需要注意的问题。通过实验评估了不同参数对性能的影响以及在不同的稀疏矩阵下同cusparse进行了比较，在部分矩阵上性能能够超越cusparse。但由于没有考虑负载均衡，在非均匀网格上，与cusparse有一定的差距。

      审核编辑：彭静