gemv优化总结

perfxlab 2023-05-25 760

描述

有朋友来信说：

1. “除了以NVIDIA（英伟达）为例，能不能谈点国产GPU优化的经验分享？”

2. “老讲国外的东西，你们能不能支持一下国产CPU和加速卡？“

这里解释一下原因：

1. N卡的资料和环境大家都比较好找，对于学习GPU并行优化编程的朋友比较友善。

2. 暂时受限于商业保密，我们相信后续会逐步开放起来，学习的平台和环境也容易找到。到时就可以分享一些国产CPU和加速卡的优化经验出来。

------ 正文分割线 ------

本文主要是介绍如何对gemv算法进行优化。gemv，即矩阵向量乘，即计算一个矩阵A与一个向量x的乘积，这是并行计算中的经典话题。个人感觉，gemv的优化核心是需要考虑不同shape的情况，然后针对型地进行优化。本篇文章会先介绍一下针对不同shape设计不同的并行算法，然后说明一下优化思路和相关优化技巧，最后说一下实验效果，在A矩阵列数为16 128的时候，我写的gemv能拥有超越cublas的性能表现。

一、前言

首先介绍一下gemv算法。给定矩阵A和向量x，gemv需要计算两者的乘积，示意图如下：

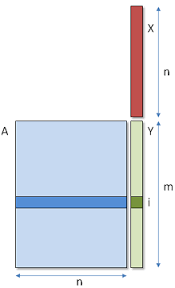
gemv

二、针对不同shape的并行算法设计

这次讲到并行算法设计，什么叫并行算法设计。每个人的理解都不太一样，在GPU中，我的理解就是：设计block和thread的workload，说白了就是要搞清楚一个block负责哪部分的计算，一个thread要负责哪部分的计算。而设计的原则就是尽可能地减少访存，提高数据的复用概率，然后让所有的处理器都满负荷地进行工作，不能浪费。

2.1 针对n=32

对于n=32的情况，我们将每个block设置为256个线程，4个warp，然后每个warp负责一行元素的计算。每个warp要对x进行访问，然后在warp内部进行一次reduce求和操作。

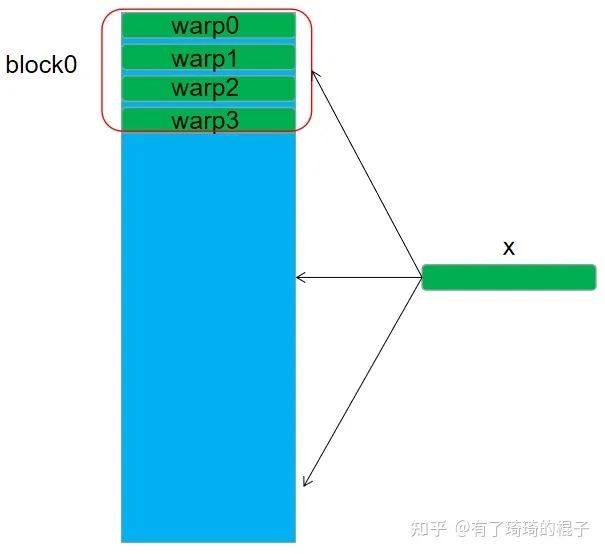
n=32

代码如下：

template 
__device__ __forceinline__ float warpReduceSum(float sum) {
    if (WarpSize >= 32)sum += __shfl_down_sync(0xffffffff, sum, 16); // 0-16, 1-17, 2-18, etc.
    if (WarpSize >= 16)sum += __shfl_down_sync(0xffffffff, sum, 8);// 0-8, 1-9, 2-10, etc.
    if (WarpSize >= 8)sum += __shfl_down_sync(0xffffffff, sum, 4);// 0-4, 1-5, 2-6, etc.
    if (WarpSize >= 4)sum += __shfl_down_sync(0xffffffff, sum, 2);// 0-2, 1-3, 4-6, 5-7, etc.
    if (WarpSize >= 2)sum += __shfl_down_sync(0xffffffff, sum, 1);// 0-1, 2-3, 4-5, etc.
    return sum;
}

// if N == 32
__global__ void Sgemv_v0( 
    float * __restrict__ A,
    float * __restrict__ x,
    float * __restrict__ y, 
    const int M,
    const int N) {
    // Block index
    int bx = blockIdx.x;

    // Thread index
    int tx = threadIdx.x;
    int ty = threadIdx.y;

    const int warp_size=32;
    int laneId= tx % warp_size;
    int current_row = blockDim.y * bx + ty;

    if(current_row < M){
        float res=0;
        int kIteration = N/warp_size;
        if(kIteration==0) kIteration=1;
        #pragma unroll
        for(int i=0; i< kIteration; i++){
            int current_col = i*warp_size + laneId;
            res += A[current_row*N + current_col] * x[current_col];
        }
        res = warpReduceSum(res);
        if(laneId==0) y[current_row]=res;
    }
}

2.2 针对n=128

对于n=128的情况，同样让warp负责一行元素的计算，但是因为每行的元素比较多，所以采用了float4进行向量化的访存。能够有更高的访存效率。

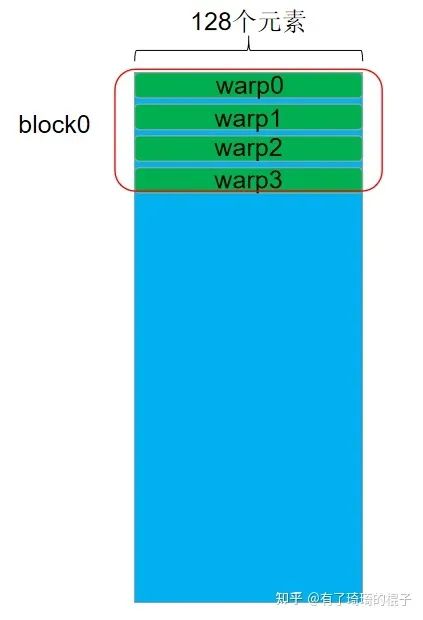
n=128

代码如下：

template 
__device__ __forceinline__ float warpReduceSum(float sum) {
    if (WarpSize >= 32)sum += __shfl_down_sync(0xffffffff, sum, 16); // 0-16, 1-17, 2-18, etc.
    if (WarpSize >= 16)sum += __shfl_down_sync(0xffffffff, sum, 8);// 0-8, 1-9, 2-10, etc.
    if (WarpSize >= 8)sum += __shfl_down_sync(0xffffffff, sum, 4);// 0-4, 1-5, 2-6, etc.
    if (WarpSize >= 4)sum += __shfl_down_sync(0xffffffff, sum, 2);// 0-2, 1-3, 4-6, 5-7, etc.
    if (WarpSize >= 2)sum += __shfl_down_sync(0xffffffff, sum, 1);// 0-1, 2-3, 4-5, etc.
    return sum;
}

// if N>= 128
__global__ void Sgemv_v1( 
    float * __restrict__ A,
    float * __restrict__ x,
    float * __restrict__ y, 
    const int M,
    const int N) {
    // Block index
    int bx = blockIdx.x;

    // Thread index
    int tx = threadIdx.x;
    int ty = threadIdx.y;

    const int warp_size=32;
    int laneId= tx % warp_size;
    int current_row = blockDim.y * bx + ty;

    if(current_row < M){
        float res=0;
        int kIteration = (N/warp_size)/4;
        if(kIteration==0) kIteration=1;
        A = &A[current_row*N];
        #pragma unroll
        for(int i=0; i< kIteration; i++){
            int current_col_vec = (i*warp_size + laneId);
            float4 current_val= reinterpret_cast(A)[current_col_vec];
            float4 current_x = reinterpret_cast(x)[current_col_vec];
            res += current_val.x*current_x.x;
            res += current_val.y*current_x.y;
            res += current_val.z*current_x.z;
            res += current_val.w*current_x.w;
        }
        res = warpReduceSum(res);
        if(laneId==0) y[current_row]=res;
    }
}

2.3 针对n=16

对于n=16的情况，让一个warp负责两行元素的计算。以warp0为例，0-15号线程负责第0行元素的计算，而16-31号线程负责第1行元素的计算。

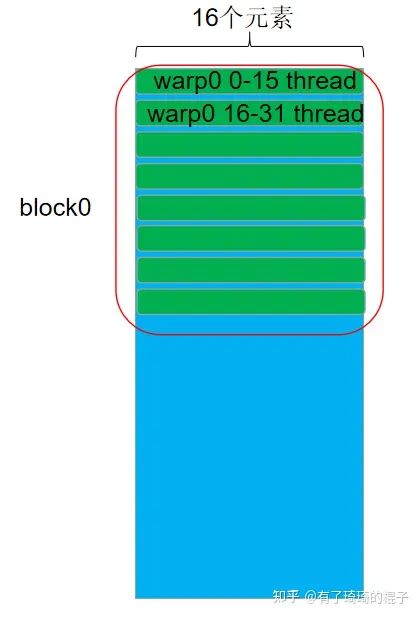
n=16

代码如下：

template 
__device__ __forceinline__ float warpReduceSum(float sum) {
    if (WarpSize >= 32)sum += __shfl_down_sync(0xffffffff, sum, 16); // 0-16, 1-17, 2-18, etc.
    if (WarpSize >= 16)sum += __shfl_down_sync(0xffffffff, sum, 8);// 0-8, 1-9, 2-10, etc.
    if (WarpSize >= 8)sum += __shfl_down_sync(0xffffffff, sum, 4);// 0-4, 1-5, 2-6, etc.
    if (WarpSize >= 4)sum += __shfl_down_sync(0xffffffff, sum, 2);// 0-2, 1-3, 4-6, 5-7, etc.
    if (WarpSize >= 2)sum += __shfl_down_sync(0xffffffff, sum, 1);// 0-1, 2-3, 4-5, etc.
    return sum;
}

// if N <= 16
template <
    const int ROW_PER_WARP
    > 
__global__ void Sgemv_v2( 
    float * __restrict__ A,
    float * __restrict__ x,
    float * __restrict__ y, 
    const int M,
    const int N) {
    // Block index
    int bx = blockIdx.x;

    // Thread index
    int tx = threadIdx.x;
    int ty = threadIdx.y;

    const int warp_size=32;
    int laneId= tx % warp_size;
    int current_warp_row = (blockDim.y * bx + ty) * ROW_PER_WARP;
    const int kWarp_size = warp_size / ROW_PER_WARP;
    int kLaneId = laneId % kWarp_size;
    int current_thread_row = current_warp_row + laneId / kWarp_size;

    if(current_thread_row < M){
        float res=0;
        int current_col = kLaneId;
        res += A[current_thread_row * N + current_col] * x[current_col];
        res = warpReduceSum(res);
        if(kLaneId==0) y[current_thread_row]=res;
    }
}

三、优化思路：

上一节说明了如何针对不同维度的n进行优化，这一节说明一下为什么要这么设计，以及这样的设计方式能够带来什么样的好处。主要考虑的因素有两个，如下：

3.1 尽可能地让warp中的32个线程忙碌

这个主要是针对n<32的情况，例如n=16，如果使用一个warp来负责一行元素的计算，那么warp中有一半的元素都是浪费的。所以让一个warp来负责多行元素的计算，这样让32个线程全部忙碌起来。

3.2 尽可能地提高访存效率

① global mem->register

将数据从global memory搬运到寄存器上时，最重要的就是考虑是不是进行了合并访存。在这里，我们只考虑矩阵数据在global mem中是地址对齐的，即n是2的多次幂。上述的三种并行实现中，warp中的32个线程都是连续地访问32个float或者128个float，因而满足了合并访存的条件，确保了global -> register的访存效率。

② shared mem->register

说到这里，可能会有读者好奇，上述的代码都没有用到shared mem。为啥要说这个点。我们可以再仔细看看上述的三种并行实现，以第2种为例，一个block中有4个warp，每个warp都需要对x进行一次global上的访存，所以一个block有4次访存。如果将x存储到shared mem中，4个warp都去访问shared mem上的x，这样的话，对于global的访存就从4次变成1次。直观上会有性能提升，但不幸的是，如果用shared mem的话，将global mem的数据搬运至shared mem需要有同步操作，这又会导致性能的下降。总的来说，使用shared mem并没有得到显著的提升，不过还是在这里说明一下。

③ 向量化访存

向量化访存就是一个老生常谈的话题了，说白了就是尽可能地使用128bit的访存指令，这个在reduce、sgemm、elementwise专题上说了很多，就不再多说。

四、实验与总结

笔者在V100上进行了实验，迭代1000次，用nsight进行了测试，性能数据如下：

sgemv	M	N	my_sgemv time(ns)	cublas(ns)	my_sgemv/cublas
v0	16384	32	10341	8386	81.1%
v1	16384	128	14284	15848	110.9%
v2	16384	16	6903	7576	109.7%

可以看出，在n=16以及n=128的情况下，都比cublas性能要好。n=32的情况要差于cublas。如果再加上向量化访存应该能够有更好的性能表现。由于我实在没时间再进行深入，有心的同学可以改改代码看看效果 :)。

审核编辑：彭静

打开APP阅读更多精彩内容