DM642上5/3提升小波的优化

在新的图像压缩标准JPEG2000中，采用9/7、5/3提升小波变换作为编码算法，其中5/3小波变换是一种可逆的整数变换，可以实现无损或有损的图像压缩。在通用的DSP芯片上实现该算法具有很好的可扩展性、可升级性与易维护性。用这种方式灵活性强，完全能满足各种处理需求。
1 提升算法
提升算法[1]是由Sweldens等在Mallat算法的基础上提出的，也称为第二代小波变换。与Mallat算法相比，提升算法不依赖傅立叶变换，降低了计算量和复杂度，运行效率相应提高。由于具有整数变换及耗费存储单元少的特点，提升算法很适合于在定点DSP上实现。
小波提升算法的基本思想是通过基本小波逐步构建出一个具有更加良好性质的新小波。其实现步骤为分解(split)、预测(predict)和更新(update)。
首先按照对原信号进行对称延拓得到新的x(n)。
分解是将数据分为偶数序列x(2n)和奇数序列x(2n+1)二个部分；
预测是用分解的偶数序列预测奇数序列，得到的预测误差为变换的高频分量：H(n)=x(2n+1)-{[x(2n)+x(2n+2)]>>1}
更新是由预测误差更新偶数序列，得到变换的低频分量： L(n)=x(2n)+{[H(n)+H(n-1)+2]>>2}
计算过程如图1所示。

2 基于DM642的优化策略
2.1 DM642的两级CACHE结构
DM642是一款专门面向多媒体处理领域应用的处理器，是构建多媒体通信系统的良好平台。它采用C64xDSP内核，片内RAM采用两级CACHE结构[4][5]，分为L1P、L1D和L2。L1只能作为CACHE被CPU访问，均为16KB，访问周期与CPU周期一致，其中L1P为直接映射，L1D为两路成组相关；L2可以由程序配置为CACHE和SRAM。
2.2 改进的算法结构
传统的小波变换都是对整幅图像作变换，先对每一行作变换，然后再对每一列作变换。用这种方式在DSP上实现该算法时效率比较低。因为DSP的L1D很小，只有16KB，不能缓存整幅图像，因此原始图像数据通常保存在速度较低的外部存储器上。这样CPU从L1D每读取一行数据时必然会产生缺失，大量缺失会严重阻塞CPU的运行，延长程序的执行时间。为了减少缺失的发生，必须将传统的变换进行改进。将原来对整幅图像的变换改为分块的变换，即每次从图像中取出一个块，先后完成行、列变换后再按照一定的规则保存到系数缓存中，如图2所示。

在这种方法中，SDRAM中的一个数据块首先传输到L2中，然后取到L1D中进行水平方向的提升，再对该块进行垂直方向的提升。这样，由于垂直提升所需的数据都在L1D中，避免了此处数据缓存缺失的产生，使总的缺失数大大降低。
2.3 数据传输
(1)SDRAM与L2间的数据传输
由于EDMA[6][7]数据传输与CPU运行相互独立，因此在L2中开辟两块缓存：EDMA在CPU处理InBuffA的同时将下一块数据传输到InBuffB，解决了CPU读取低速设备SDRAM引起的时延，如图3所示。

(2)L2与L1D间的数据传输
CPU首先访问第一级CACHE中的程序和数据，如果没有命中则访问第二级CACHE（如果配置L2的一部分为CACHE)，若还没有命中就要访问外部存储空间。在这个过程中，CPU一直处于阻塞状态，直至读取的数据有效。所以，在对L2中的数据块进行水平提升时，CPU读取每一行都会产生缺失。针对这种情况，TMS320C64x系列DSP为L1D提供了一种高速缓存缺失处理的流水处理机制。若连续多次未命中，CPU等待时间就会重叠，总体上减少了平均缺失造成的CPU阻塞时间。
因此，在CPU对数据进行水平提升前，利用缺失流水技术，将当前数据块全部读取到L1D中，随后再对该数据块进行水平提升，则不会再发生缺失，并可提高运算速度。
2.4 L1P与L1D性能优化
L1D是两路成组相关，每组8KB，总容量16KB。CPU一次处理的数据不应超过8KB，并且所有的原始数据都连续存储在同一CACHE组中；程序的中间过程数据保留在预分配的另一个CACHE组中。
数据读取到L1D之后，首先由8位扩展成16位，然后对这些数据进行水平提升，只要这些数据能保留在L1D中，随后进行的垂直提升就可以完全避免缺失。因此，数据块的大小是由中间过程数据决定的，所有中间过程数据加起来不能超过8KB，选取数据块是32×32。
当多个函数映射到L1P的同一个CACHE行时就会引起冲突缺失，所以必须合理放置这些函数。由于实现提升的全部函数加起来不超过16KB，因此，如果能将这些函数安排在一个连续的存储空间内，就可以完全避免由冲突引起的L1P缺失。可以在cmd[8]文件的SECTIONS中添加一个GROUP，然后将频繁调用的函数放到GROUP中：
SECTIONS
{
GROUP > ISRAM
{
.text：_horz
.text：_vert
.text：_IMG_pix_pand
…
}…}
2.5 程序优化
由前面的分析可知,对图像进行提升小波变换时,需要对其四个边界进行延拓。延拓方式采用图1所示的对称延拓，其中左边与上边需要多延拓一个点。而对图像中的一个块进行提升变换时，其延拓的应该是与该块相邻的四个块数据的边界数据，如图4所示。

边界延拓主要是用于计算高频系数。分析发现，水平提升时，当前数据块每一行的最后一个高频系数与下一个块在该行的第一个高频系数相同。所以只要把当前块的这些系数保存起来，在对下一块进行水平提升时第一个高频系数就不需要再进行计算，因此也就不需要再对其左边界进行延拓了。垂直方向的提升也是同样的道理。在程序中添加两个数组，分别用于存放当前块的每一行与每一列的最后一个高频系数。采用这种方法就可以降低程序的复杂度，提高执行效率，减少缺失的发生。
像素扩展函数pix_pand[9]是采用TI的IMGLIB算法库。水平提升与垂直提升函数均由作者用线性汇编语言编写，充分利用64x系列DSP的半字处理指令，采用半字打包技术，最大限度地提高程序的执行效率。
水平提升时，将每行的数据重新排序，变成如图5所示的结构。

使用C64x的ADD2、SHR2和SUB2等半字处理指令，将如下的两个运算并行执行：
 H(1)=B-[(A+C)>>1]
 H(2)=D-[(C+E)>>1]
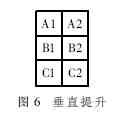
垂直提升时则可以安排多列的计算并行执行，如图6所示。
 H1(1)=B1-[(A1+C1)>>1]
 H2(1)=B2-[(A2+C2)>>1]
 

 

3 仿真结果
表1列出了CPU读取L1D时产生的缺失数。其中，水平方向的缺失不可避免。由于要对数据块的右侧和底部进行边界延拓，所以在水平方向的缺失数比传统方法略高；而在垂直方向上，该算法完全避免了缺失的发生。

表2列出了几种方法的计算性能。由于本文采用了多种优化技术，运算速度提高了4～10倍。试验证明这些方法十分有效。