

聊一聊门函数/脉冲函数的时频特性
电子说
1.4w人已加入
描述
今天聊一聊矩形脉冲,谈他只因为常见,工作中常用。
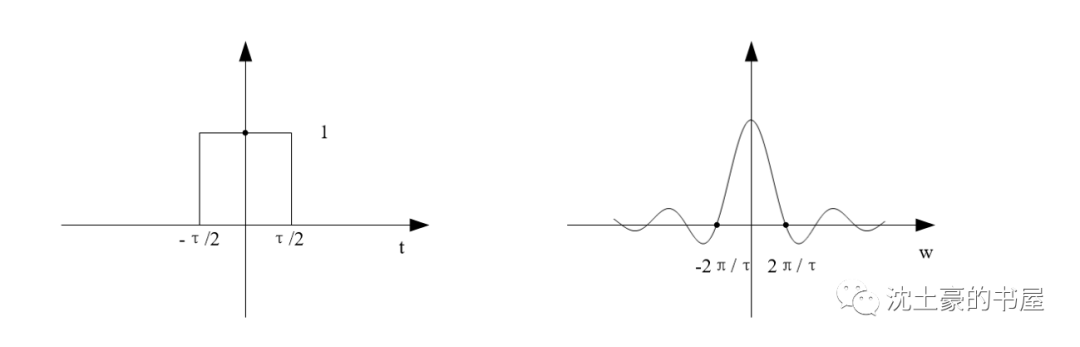
左图是个门函数,宽度为τ,高度为1,自变量t。
右图是门函数经过傅里叶变换的频谱密度函数
F(jw),自变量w。
两种变换对等,包含信号的所有信息量,仅仅是一种数学的变换域。
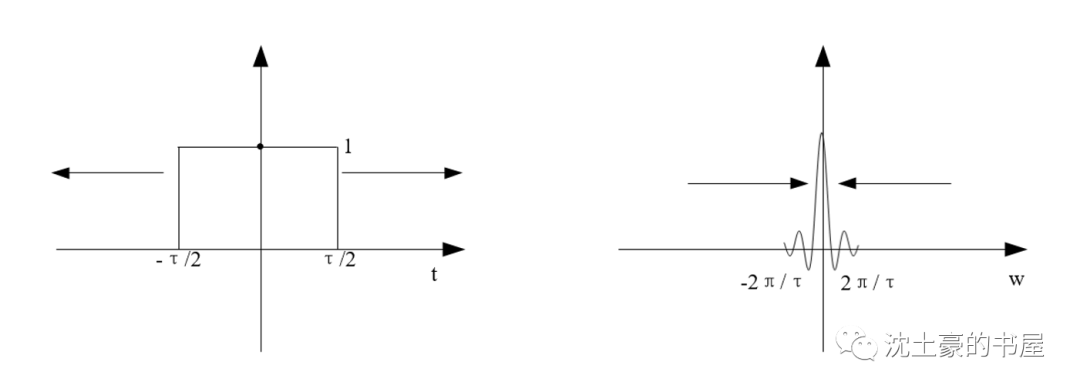
其傅里叶变换对如下式:
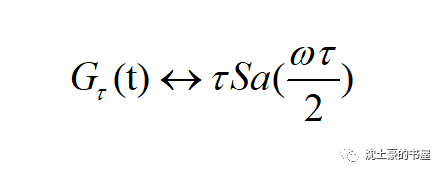
case1:
我们把门宽度缩小,即τ→0,或者很小很小,获得一个尖脉冲。(研究它的目的是尖峰噪声,都是小的脉冲,振荡的,时间宽度小的,尖刺的…)
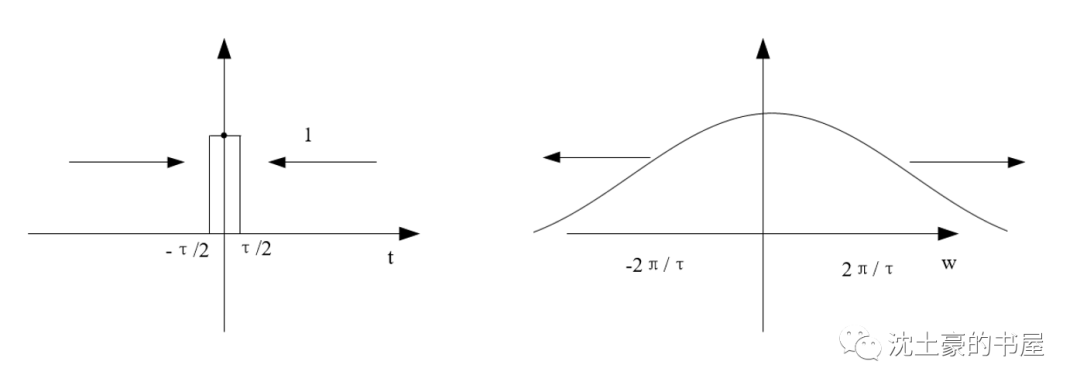
长的很像冲激函数吧~就高度不一样嘛
再看看冲激函数的FT,正好是1。
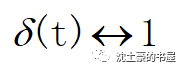
我们把门函数的FT即τSa(wτ/2),令τ趋于0,数无形时少直觉,右图一看,第一过零点直接趋于无穷大,Sa()函数中间凸起来的区域一条直线~不就长得像1吗?
case2:
我们把门宽度放大,即τ→很大,或者很大很大,获得一个直流信号。
再看看直流信号的FT,是个冲激。
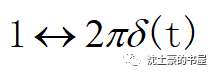
我们把门函数的FT即τSa(wτ/2),如果忽略前面的系数τ,并令τ趋于+∞。数无形时少直觉,右图一看,第一过零点直接趋于无穷小,Sa()函数中间凸起来的区域逼近于0~不就长得像冲激函数吗?
case3:
由尺度变换公式
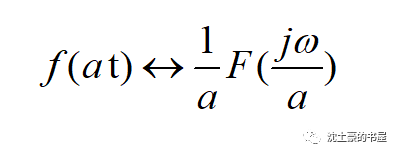
得
时域压缩信号,将会使得频谱密度函数频率轴伸展,信号的频率分量会 向高频扩散 。
时域扩展信号,将会使得频谱密度函数频率轴收缩,信号的频率分量会 向低频聚集 。
或者说:对于一个脉冲信号,信号越窄,频谱密度函数 收敛性变差 ,Sa()函数第一过零点带宽往后推,幅度较高的频率分量往后搬移。
以后应当有认知:
- 尖峰噪声具有高频特性,尖峰越窄,信号带宽越高。
- 时域观察即是尖峰噪声振荡周期/脉冲宽度。
- 频域观察即使频谱密度函数的分布情况。
REF ADI一张图

- 上图DCDC噪声,开关噪声脉冲窄,能量小,信号带宽高。
- 纹波噪声,振荡周期T大,脉宽大,能量较开关噪声大,信号带宽等于1/T。
声明:本文内容及配图由入驻作者撰写或者入驻合作网站授权转载。文章观点仅代表作者本人,不代表电子发烧友网立场。文章及其配图仅供工程师学习之用,如有内容侵权或者其他违规问题,请联系本站处理。
举报投诉
全部0条评论

快来发表一下你的评论吧 !

