

介绍一下FIR滤波器的使用
电子说
1.4w人已加入
描述
1. 滤波的目的
在信号的实时处理中,滤波是十分必要的,因为信号中难免会由于各种原因混入噪声,干扰我们对信号进行分析。
这里强调了“实时”,是因为在一些场景中,我们可能需要对信号进行离线的、交互式的分析,此时仅仅是对原始信号进行采集即可,无需软件 进行滤波,只需要硬件在采集信号时做一下抗混叠滤波即可,这种场景不是本文所关心的。
在更多的场景下,比如我们的运动手表、手环在处理ppg信号计算心率时,是会进行实时计算的,那么就会进行实时滤波处理:因为大多数人的心率频率在0.7~3.6Hz范围内,至少在这之外的频率会在计算心率之前滤除掉。
2. 信号模拟
比如我们要处理一个信号,但是我们仅仅关心信号100Hz以下的频段,这时我们就需要一个低通滤波器了,此时我们先模拟出一个包含5Hz和3000Hz频率成分的信号,假设信号采样频率为8192,采样时间为1秒,共计8192个点。信号生成和展示的代码如下:
import numpy as np
from numpy import cos
import matplotlib.pyplot as plt
pi = np.pi
t = np.linspace(0, 1, 8192)
signal = 3 * cos(2 * pi * 5 * t + pi/3) + 7 * cos(2 * np.pi * 3000 * t + 3/8*pi)
plt.figure()
plt.plot(t, signal)
plt.show()
我们生成了这样的一个信号:
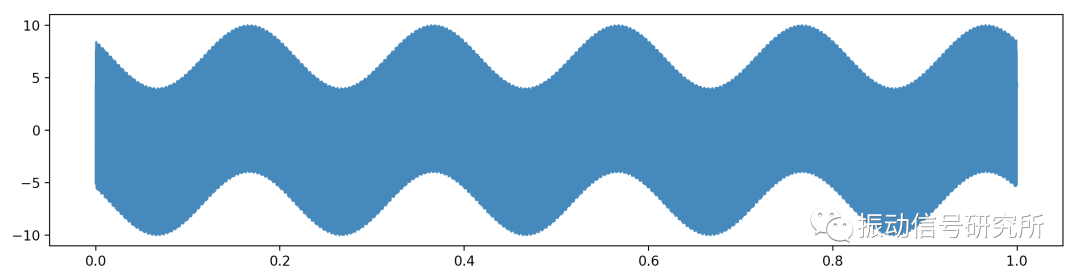
生成的信号
3. FIR滤波器系数生成
这一步可以使用matlab进行辅助,本文仅仅是想要一个截止频率为10Hz的FIR低通滤波器,步骤如下:
- 打开matlab;
- 点击"APP";
- 找到滤波器设计工具,并点击;
- 选择响应类型、设计方法、阶数等。
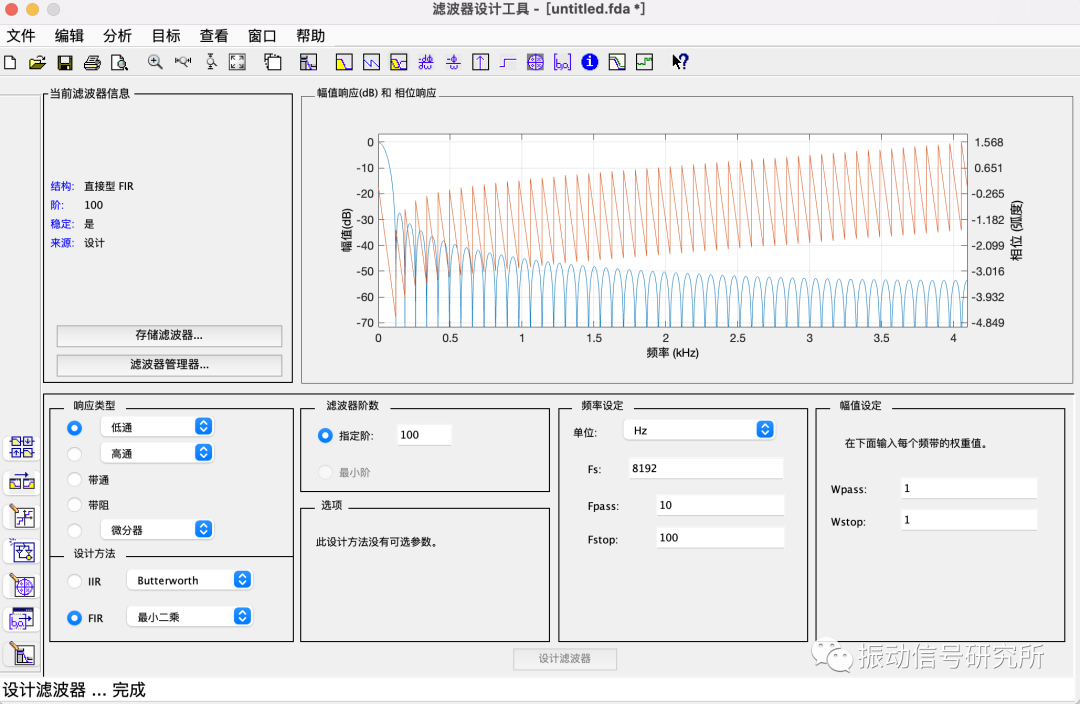
辅助设计界面
- 点击“文件” 、“导出”、“系数文件”,导出系数文件,我把导出的系数(FIR低通滤波系数仅有分子)画出来后如下图:
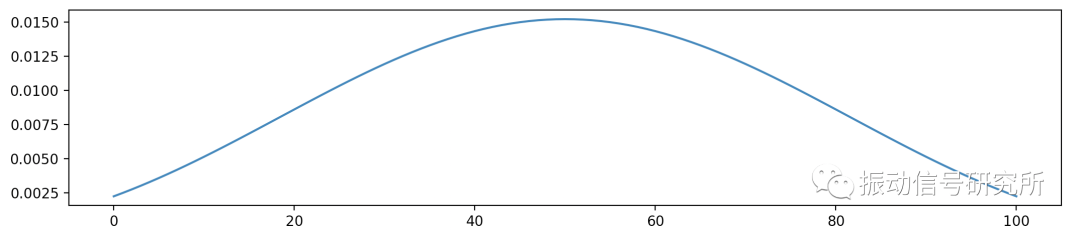
系数波形图
3. FIR滤波原理
采用FIR进行滤波,从操作上看是进行卷积操作,对上述滤波器的系数进行FFT变换即可窥见一斑:
import numpy as np
import matplotlib.pyplot as plt
# b = [......] 101个系数组成的列表,此处省略
delta_f = 1
plt.plot([delta_f * i for i in range(4097)], abs(np.fft.rfft(b, 8192))) # 单边FFT
plt.show()
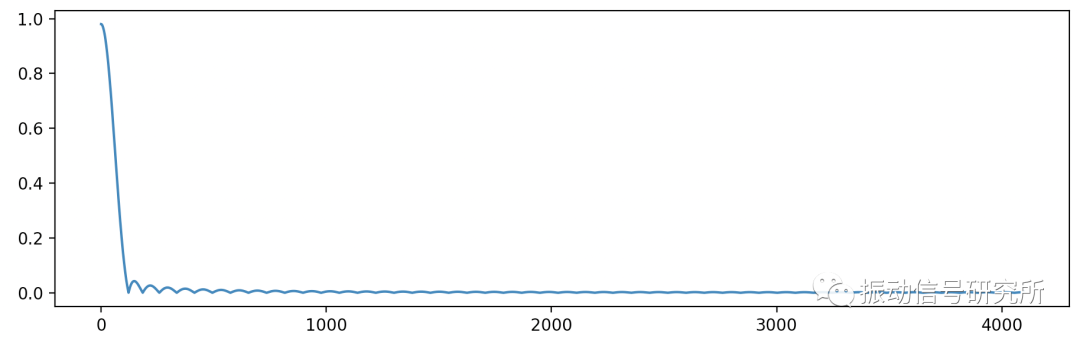
系数的傅里叶变换
这里得到的就是滤波器的幅频响应曲线,和滤波器辅助设计工具中所展示的幅频响应曲线是一致的。
4. 滤波计算代码与结果
把第二步生成的信号中高于100Hz的频率成分(即3000Hz的成分)滤除,得到的结果如下图所示,在结果的开头和结尾产生了失真,这是因为在卷积运算过程中,在刚开始和结尾计算时有效信息不足进行了补零操作导致的。
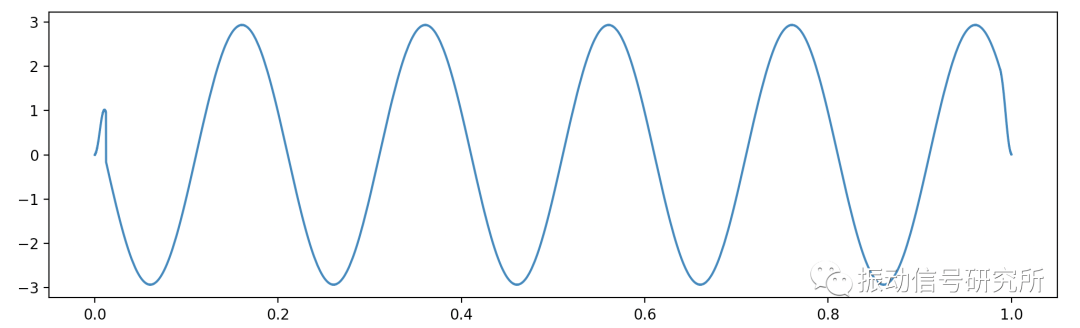
滤波的结果
这一步的运算代码如下:
import numpy as np
from numpy import cos
import matplotlib.pyplot as plt
from filter_coeff import b
pi = np.pi
t = np.linspace(0, 1, 8192)
signal = 3 * cos(2 * pi * 5 * t + pi/3) + 7 * cos(2 * np.pi * 3000 * t + 3/8*pi)
fir_len = len(b)
res = []
for i in range(len(signal)):
print(i)
temp = 0
if i < fir_len:
data = (fir_len-i) * [0] + signal[0:i].tolist()
elif i > len(signal) - fir_len:
data = signal[i:].tolist() + (fir_len - len(signal) + i) * [0]
else:
data = signal[i:i+fir_len]
for j in range(fir_len):
temp += b[j] * data[-j-1]
res.append(temp)
plt.figure()
plt.plot(t, res)
plt.show()
声明:本文内容及配图由入驻作者撰写或者入驻合作网站授权转载。文章观点仅代表作者本人,不代表电子发烧友网立场。文章及其配图仅供工程师学习之用,如有内容侵权或者其他违规问题,请联系本站处理。
举报投诉
-
IIR滤波器和FIR滤波器的区别2023-06-03 20502
-
FIR滤波器和IIR滤波器的区别与联系2022-12-30 5138
-
并行FIR滤波器Verilog设计2020-09-25 2567
-
FIR滤波器与IIR滤波器到底有什么区别2020-08-09 33699
-
如何设计低通FIR滤波器2018-08-23 5974
-
FPGA的FIR抽取滤波器设计详细教程2018-04-19 2746
-
FIR滤波器的FPGA设计与实现2017-12-21 1232
-
详解FIR滤波器和IIR滤波器的区别2017-05-03 2757
-
基于MATLAB的FIR滤波器设计与滤波2016-12-14 1396
-
fir_滤波器sourc2015-12-14 565
-
DSP in FPGA:FIR滤波器(一)2014-06-27 10738
-
高阶FIR正交镜像滤波器的设计2011-08-29 813
-
什么是fir数字滤波器 什么叫FIR滤波器2008-01-16 17573
全部0条评论

快来发表一下你的评论吧 !

