模拟无源滤波器设计(九)-Gaussian滤波器设计详解

 

文章详细对高斯滤波器的综合设计进行讲解，解释如何从时域无过冲推导出高斯滤波器的。并且深入探讨了高斯滤波器的零极点分布。最后介绍基于Matlab的滤波器设计软件，以低通、带通滤波器为例，展示其功能，并给出Github相关链接。

高斯滤波器特点和用途

高斯滤波器(Gaussian Filter)滤波器是具有最佳时域特性的滤波器，其幅频曲线具有高斯函数(Gaussian function)曲线分布特性，对阶跃响应无任何过冲，实际应用中高斯逼近滤波器和贝塞尔逼近滤波器特性非常类似，随着两者阶数增加两者表现将趋于一致，高斯滤波器的能够高保真的传输时域信号特点使得它在时域应用中很重要，比如示波器设备，雷达设备等。当然现在在数字图像处理中应用也非常广泛。

高斯滤波器逼近

约束

• 1, 是阶多项式(可实现性，在频率增益为0)
• 2, (低通定义，在频率为0的位置增益为1)
• 3, (定义低通半带宽)
• 4, 给定一个阶跃信号, 无过冲
• 5, 给定一个阶跃信号, 有最快上升沿(按阶跃信号导数所生成的钟形曲线的半宽度最小定义)

傅里叶变换

首先我们需要复习下连续时间傅里叶变换：

 

如下左图是一个脉冲信号，右图是这个脉冲信号的连续傅里叶变换结果。

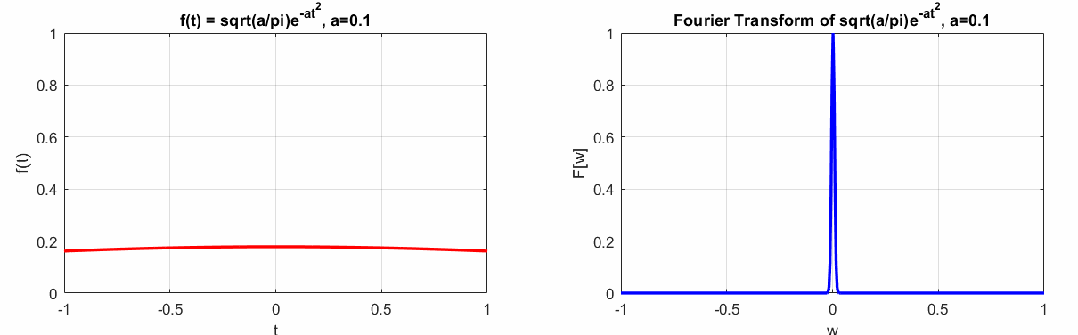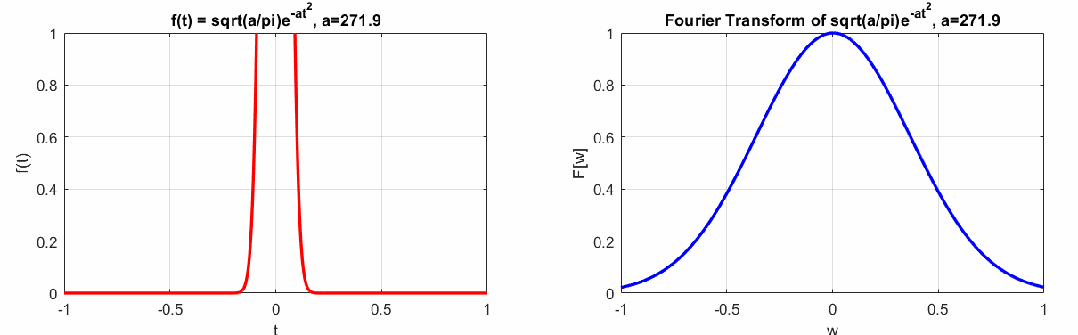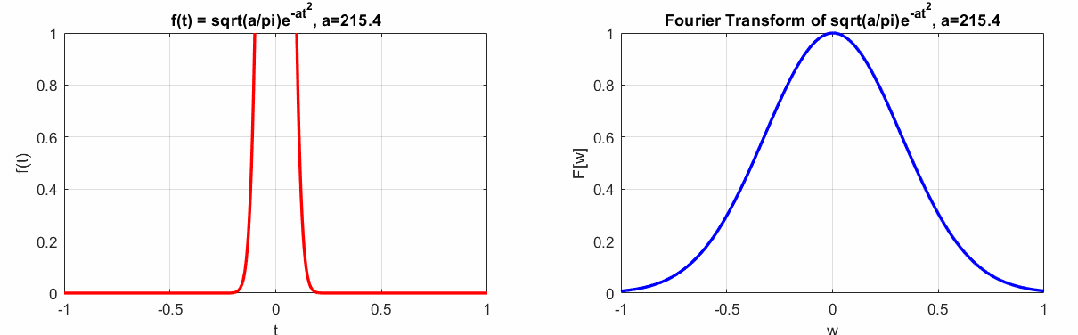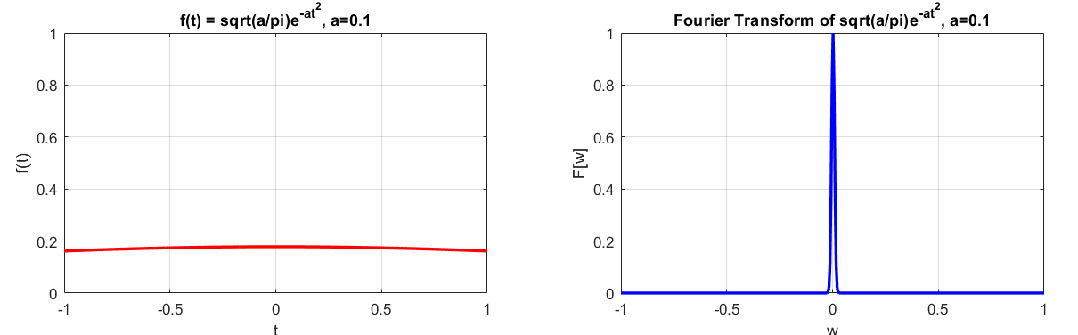
可以看到左边曲线和右边曲线的胖瘦关系相反，若左边时域脉冲信号越瘦，右边越胖，反之左边越胖，右边越瘦，这个特点即时间-频域的不确定性原理(类似海森堡动量-位置的不确定性原理)，即时频特性不能兼得(感兴趣的同学可以参考时频分析的相关书籍)。

时域阶跃到频响

从约束4可以看到一个阶跃信号无过冲，这是一个时域信号，而最后我们要求解的频域响应，所以这里必然要用到时域-频域转换，即前面提到的傅里叶变换，以下是一个阶跃信号如何变换为一个频域响应的：

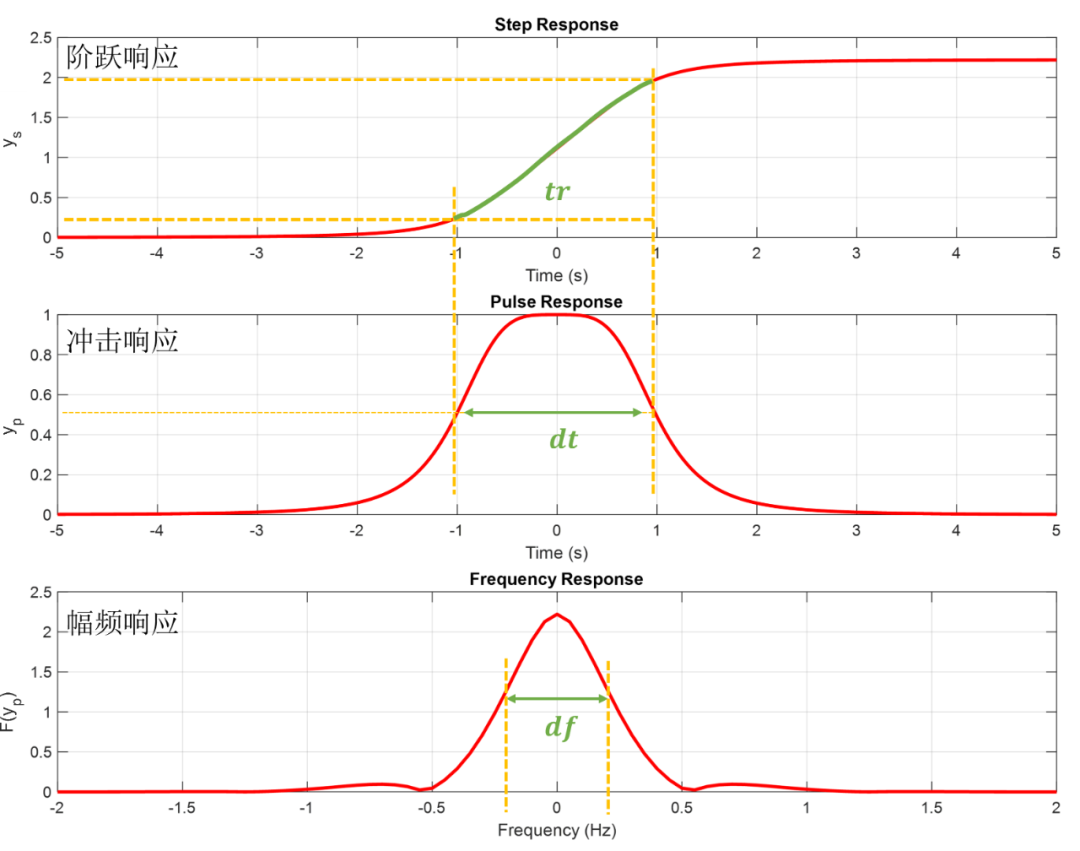
首先我们要对阶跃响应进行微分，即可得到冲击响应，然后运用连续傅里叶变换(式1)将冲击响应转换到频域，即可得到频响。

这里有一个重要的点是，阶跃响应的上升时间的计算，如图中的阶跃信号所展示的，表示上升时间，所对应了冲击响应的脉冲宽度，这里的时域脉冲宽度选择了脉冲的半时间宽度。而幅频响应的频域宽度代表了这个脉冲系统响应的带宽，这里的频域脉冲宽度选择了脉冲的半频域宽度(即-6dB截止频率点)。

有了上述铺垫，我们可以求解出一个无过冲的最佳时频滤波器了，从上面约束可以得到，当频域宽度一定情况下，我们希望得到的阶跃响应无过冲，并且上升时间(即冲击响应宽度)最小的系统函数，那么满足这样的系统函数是什么呢？

这要求，Gabor给出了答案(有关这个问题的讨论可以参考)，满足这个时频最佳响应的滤波器即高斯滤波器(Gaussian Filter)，即系统函数是:

 

换句话说：在给定的带宽下，其阶跃响应上升时间最短且无过冲的滤波器就是高斯滤波器。

注意这里的带宽和上升时间的定义与通常定义的不同。

高斯滤波器

高斯滤波器是一类特殊的理想滤波器，其地位和矩形滤波器(Rectangular Filter, 也叫理想滤波器, Ideal Filter, 砖墙滤波器, Brick-wall Filter, sinc滤波器)相当，是无法通过多项式直接拟合得到的，只能通过函数逼近的方式得到，现在我们总结下现有滤波器设计。

总共有两类滤波器综合如下(当然这个图还可以扩展)：

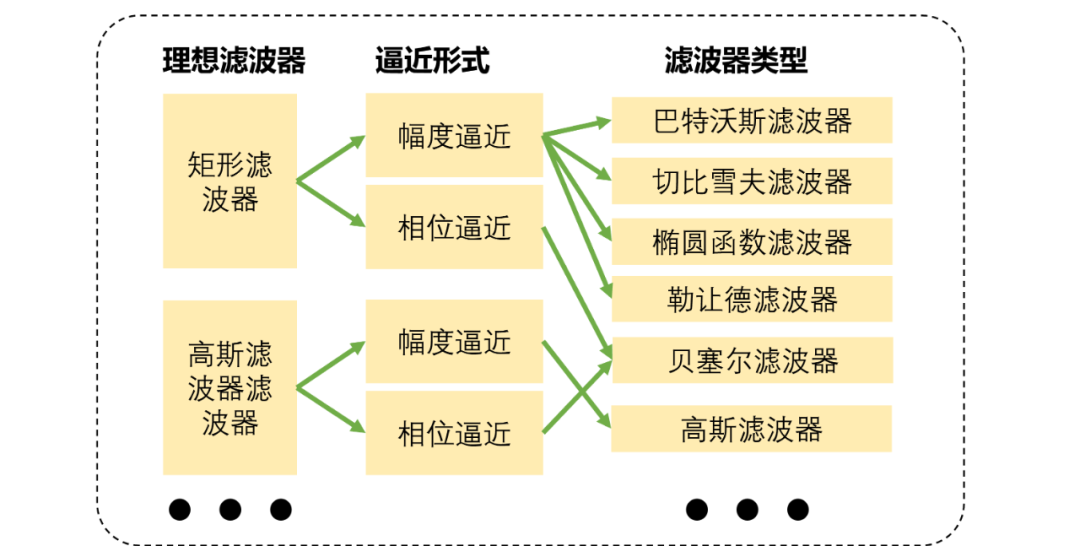
高斯滤波器综合全流程如下：

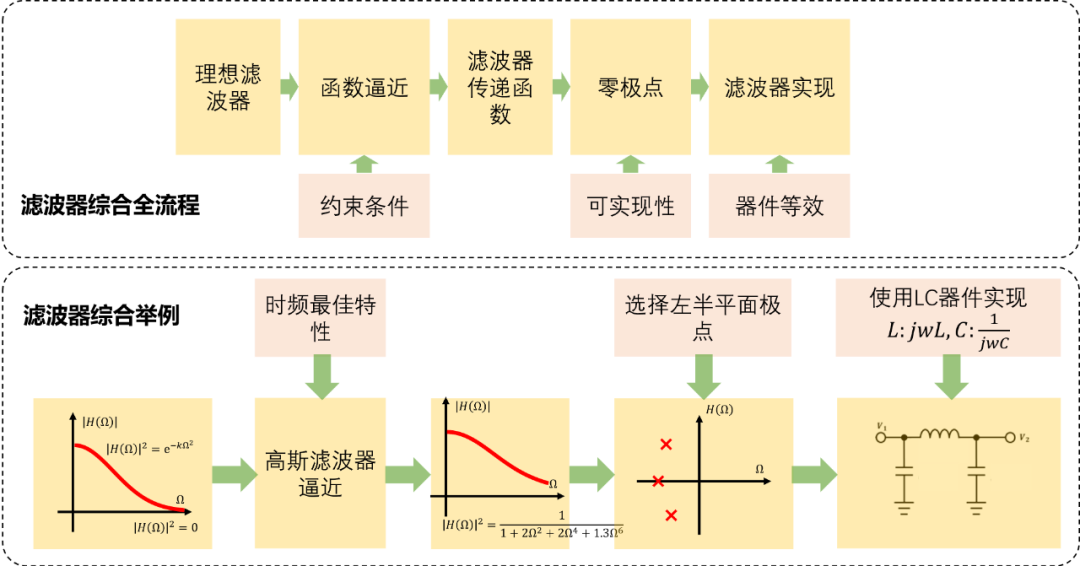
高斯滤波器逼近

高斯滤波器是理想滤波器，其原因可以用如下动图说明，图中高斯滤波器曲线是红色曲线(式2)，在对数-对数坐标系下这样高斯滤波器就是指数函数，而蓝色曲线是有理多项式逼近，在对数-对数坐标系下，高频范围是线性的。使用一个线性函数去逼近指数函数显然是不能完成的，所以无法使用有限阶的有理多项式来逼近高斯函数。

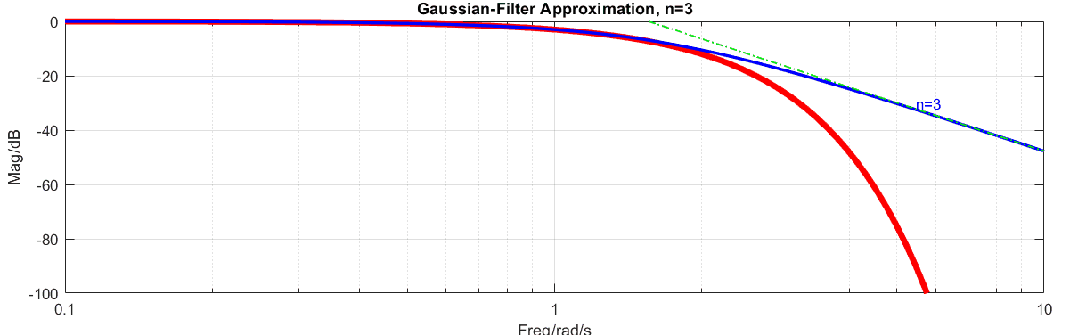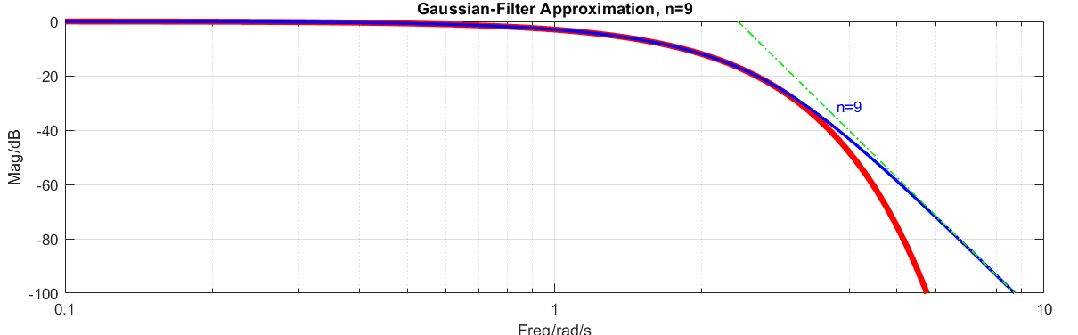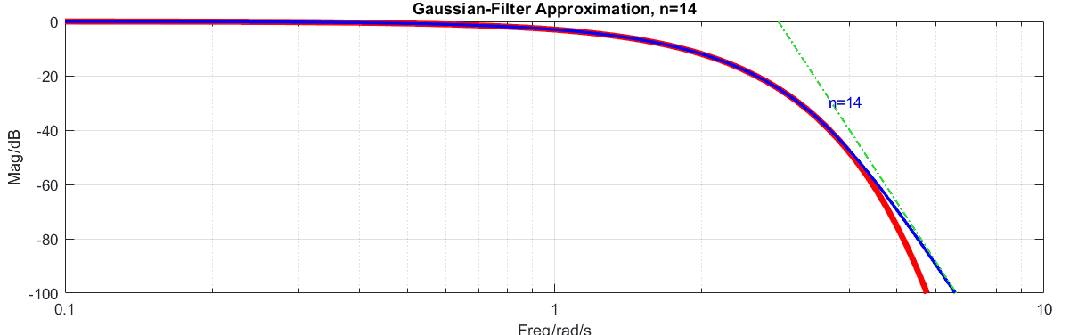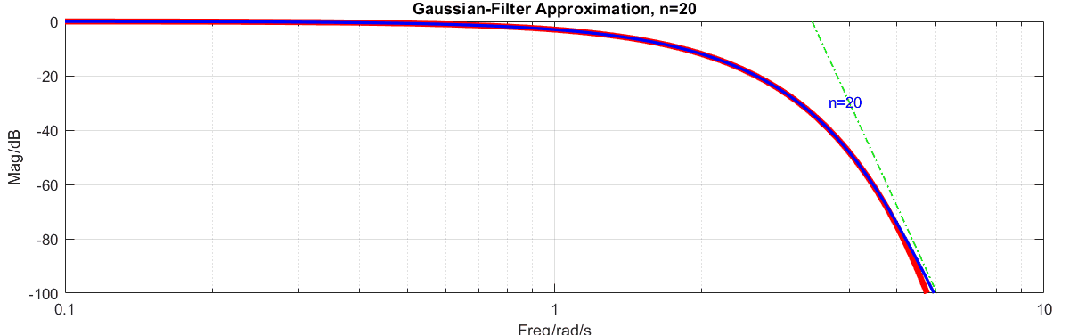
我们只能使用多项式尽可能的去逼近高斯滤波器，这里常用的方法是泰勒展开，公式如下：

 

当我们系统中要求频率在时为其截止点时：

 

令得到前7阶高斯滤波器系数为()：

滤波器阶数
1
2
3
4
5
6
7

在s平面取其左半边极点得到前7阶高斯滤波器系数为()：

滤波器阶数
1
2
3
4
5
6
7

前7阶高斯数滤波器极点为()：

滤波器阶数
1
2
3
4
5
6
7

同Bessel滤波器一样需要有高斯滤波器带宽修正系数：

滤波器阶数	2	3	4	5	6	7
极点修正系数

注：手机党可横屏查看表格

高斯滤波器零极点

和贝塞尔滤波器极点符合反斯托克斯线类似，高斯滤波器极点分布符合某个曲线，这个曲线公式为:

 

其中是实轴, 是虚轴，其来源于的泰勒展开部分展开式零点的渐进线——Szegő曲线，Szegő曲线分布（注意下图横坐标为虚轴，纵坐标为实轴）如下，其极点分布在一个水滴型曲线上，具体公式是(注意：这个是个近似公式，当越大，精确度越高)：

 

上式也可以化为和的形式：

 

这个公式只能在趋于无穷大时才和实际零点重合，而且趋近速度很慢，这里对其进行拟合得到一个新近似公式(若希望得到更高精度的逼近可以参考，关于指数函数泰勒级数求和零点分布问题也是一个研究热点)：

 

效果如下动图所示(其中New Fit：式8的曲线；蓝色曲线：Szego曲线的式6a；黑色的圆圈是Szego曲线的式6b，绿色盘面即指数泰勒展开式零点分布区域，红色点是不同n下的实际零点位置)：

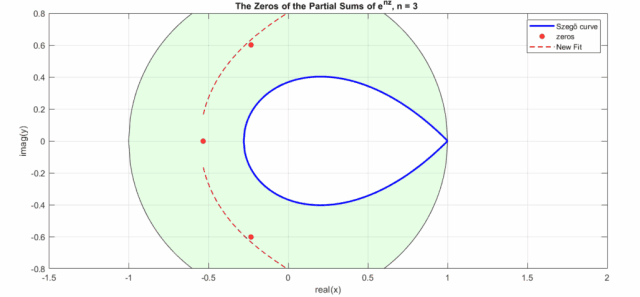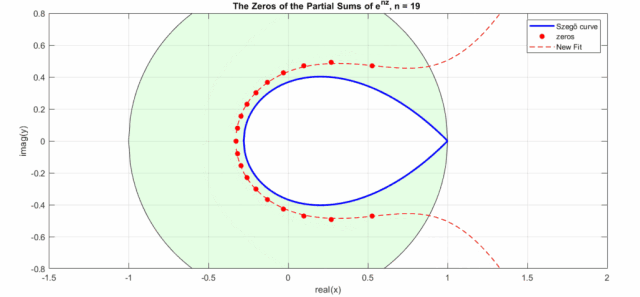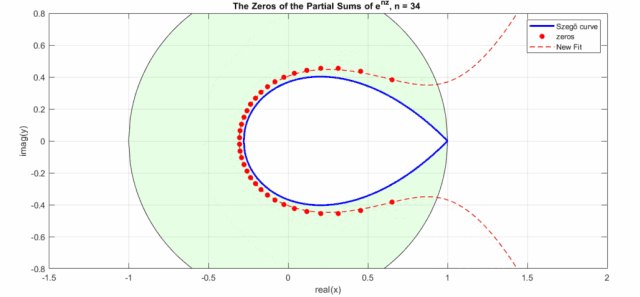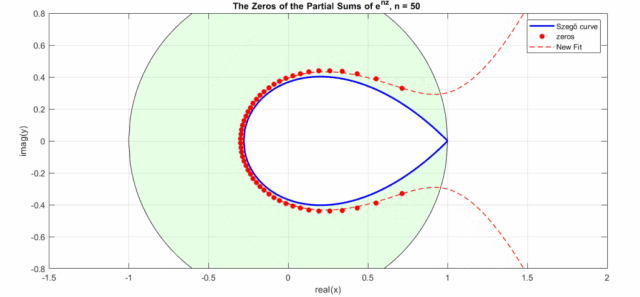
有了的零点，那么高斯函数的零点也就可以简单的通过来求解，即:

 

令且那么得到：

 

通过这个变换后可以将指数函数的零点转换为高斯函数的零点：

 

上面的公式有所以，平方后将零点映射到虚轴(这里是轴)的右半部分。

按照转换公式11，可以得到修正后的高斯函数零点为：

 

下图是修正后的高斯函数(式12)零点曲线图(注意，这里图横坐标为虚轴，纵坐标为实轴。蓝色为Szego曲线式6经过式11映射后的曲线，红色虚线式式12表示的曲线，红色点是高斯函数泰勒级数展开部分和的零点分布)：

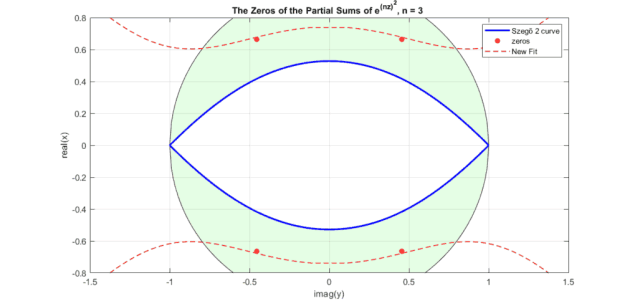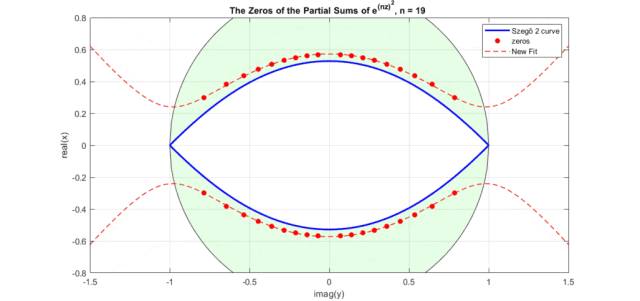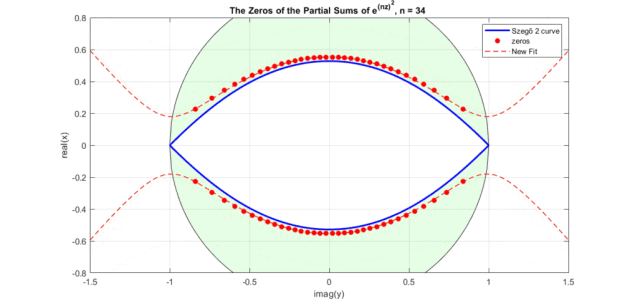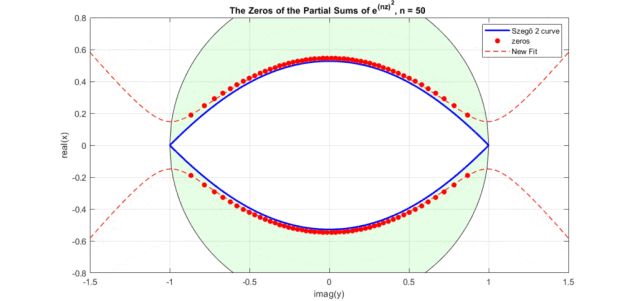
图中出现了和Bessel多项式零点非常相似的图形，是一个眼型曲线。

PS.通过平方，这个曲线变得更加对称了，而且对称点为原点。

下面是四种不同滤波器极点的对比(以上讨论是零点，滤波器中由于求了个倒数，故零点变极点)，在这里我们得到了一只完整的眼睛。蓝色曲线是切比雪夫I型滤波器极点分布，是瞳孔(Pupil)；品红色曲线是巴特沃斯滤波器极点分布，是眼球(Eyeball)；青色曲线是贝塞尔滤波器极点分布，是眼睑(Eyelash)；红色曲线是高斯滤波器极点分布，是眼皮(Eyelid)。

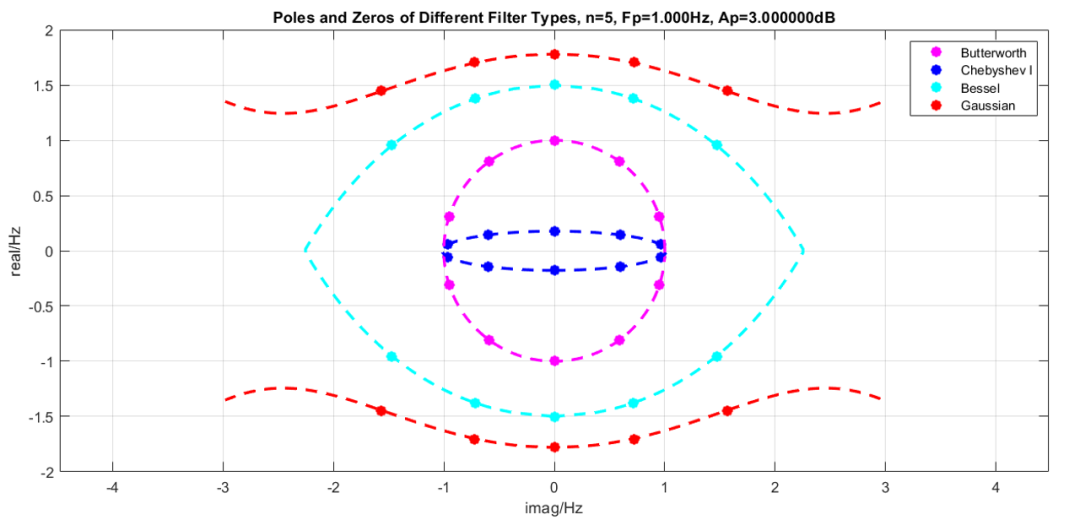
高斯滤波器的过冲

高斯滤波器在理想情况下无过冲，原因是高斯函数的逆傅里叶变换也是高斯函数，也是时域的冲击响应，高斯函数恒定大于0，即积分后无斜率小于0的点，所以没有过冲。但是使用泰勒展开高斯函数逼近后的滤波器却是有过冲的，如下图显示了不同滤波器的过冲(纵坐标改为对数用于不同滤波器的对比)：

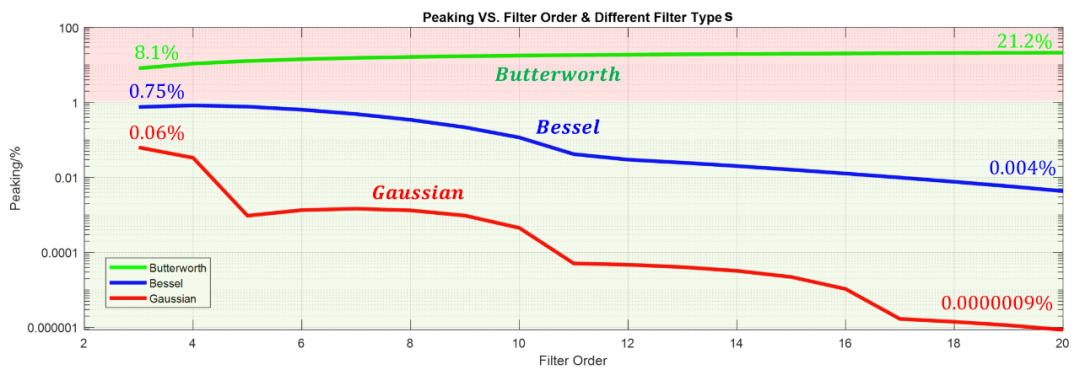
从中可以看到巴特沃斯滤波器的Peaking随着阶数增加而增加，但是贝塞尔和高斯滤波器随着阶数的增加Peaking是减小的！而且从趋势看到，当后，高斯滤波器和贝塞尔滤波器的过冲都会趋近于0。

高斯滤波器综合

高斯滤波器综合和巴特沃斯滤波器一样，属于全极点滤波器，所以这里仅仅列出一个3阶高斯滤波器综合实例，以供参考：

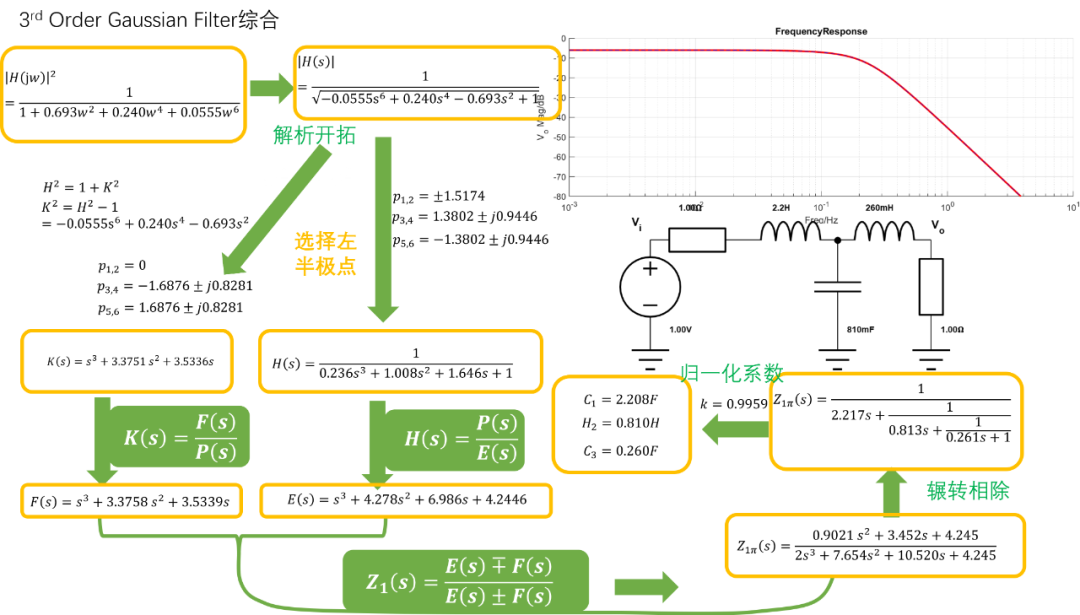
对于高斯滤波器，其综合出来的电路器件值和贝塞尔滤波器器件值非常相似：

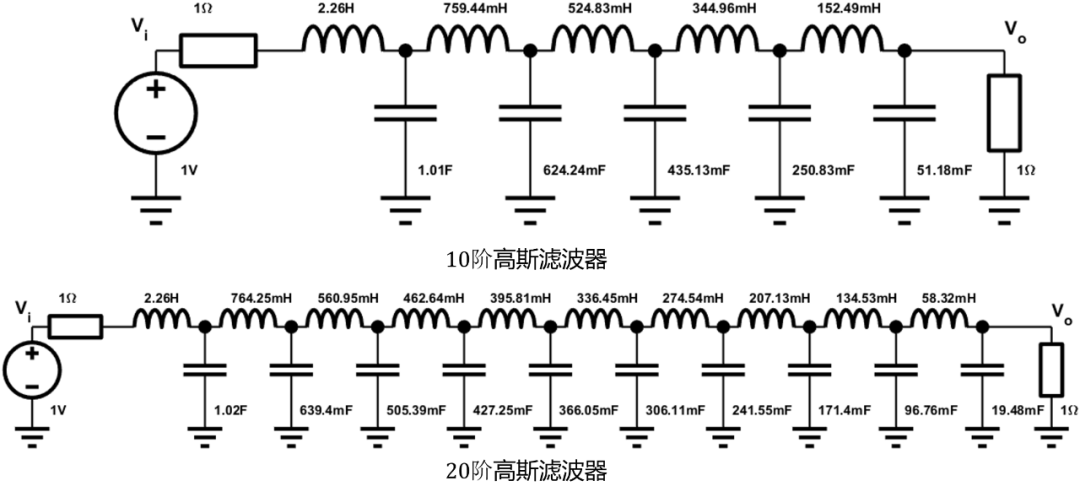
可以看到滤波器第一个器件值几乎是相等的，而且距源越远器件值越小，下图绘出了2-20阶低通高斯滤波器系数图，可以看出随着阶数的增加，前级器件值非常接近。

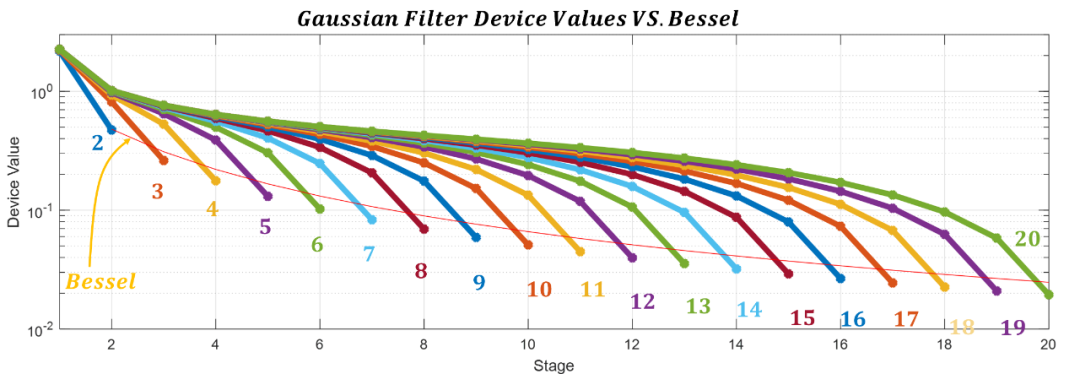
对比贝塞尔滤波器器件值而言，高斯滤波器器件值要小些。

任意负载条件下的高斯滤波器综合

这里需要求解特征多项式，即需要求解(这里有关概念可以参考滤波器设计的逼近方法 - Butterworth, Chebyshev, Elliptic)：

 

式中的定义参考模拟无源滤波器设计（六）-Chebyshev滤波器设计详解中关于任意负载条件下的求解公式。

不同滤波器通带类型之间的转换

只要有了低通原型, 其他滤波器通带类型之间的转换同Butterworth滤波器模拟无源滤波器设计（五）-Butterworth滤波器设计详解。

高斯滤波器设计软件

基于Matlab的appdesign工具开发了一套滤波器设计软件, 主要特点是：

• 支持高斯滤波器(Gaussian Filter)、贝塞尔滤波器(Bessel Filter)、椭圆函数滤波器(Elliptic/Cauer Filter)、切比雪夫滤波器(Chebyshev I)、逆切比雪夫滤波器(Chebyshev II, Inverse Chebyshev)、巴特沃斯滤波器(Butterworth)设计
• 支持4种不同滤波器通带类型(LPF,HPF,BPF,BRF)设计
• T型和PI型结构滤波器随意切换
• 可以设置阻带衰减决定滤波器阶数
• 可以设置通带衰减来综合滤波器
• 可以随意配置负载和终端阻抗, 并支持一端接载(源端电阻短路, 源端电流源, 终端开路, 终端短路)设计
• 可以幅频响应分析、零极点分析、瞬态分析
• 可以显示理想频率响应、零极点和实际仿真的的频率响应、零极点
• 可以支持实际标准器件逼近设计

Gaussian LPF设计举例

设计一款-3dB截止频率为1GHz, 7阶低通Gaussian滤波器，输入输出阻抗为50欧姆，设计过程如下：

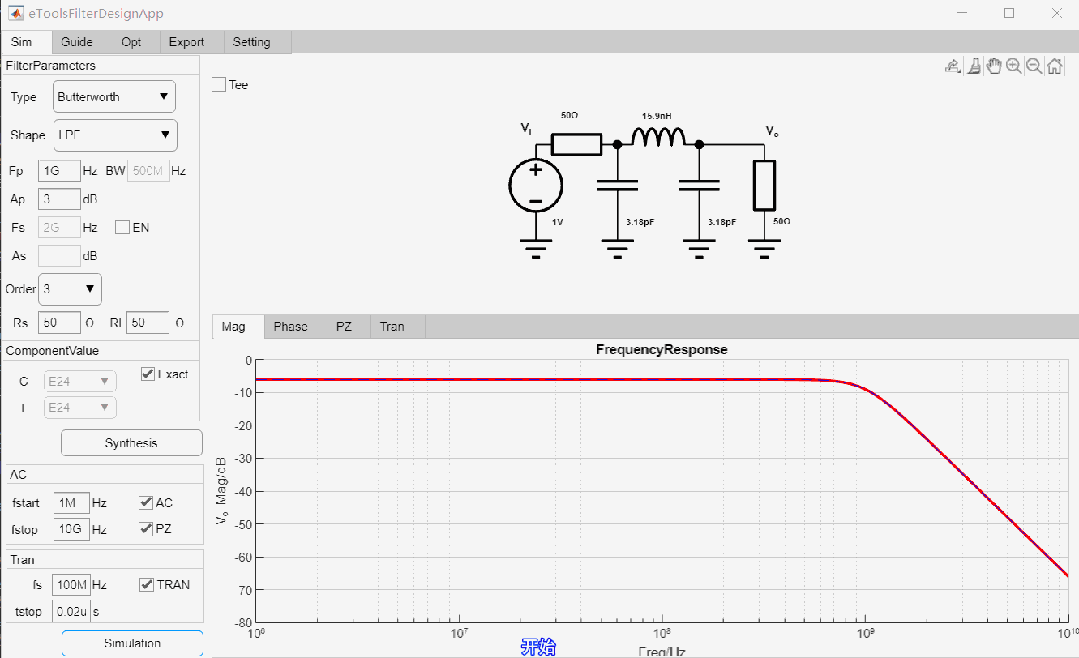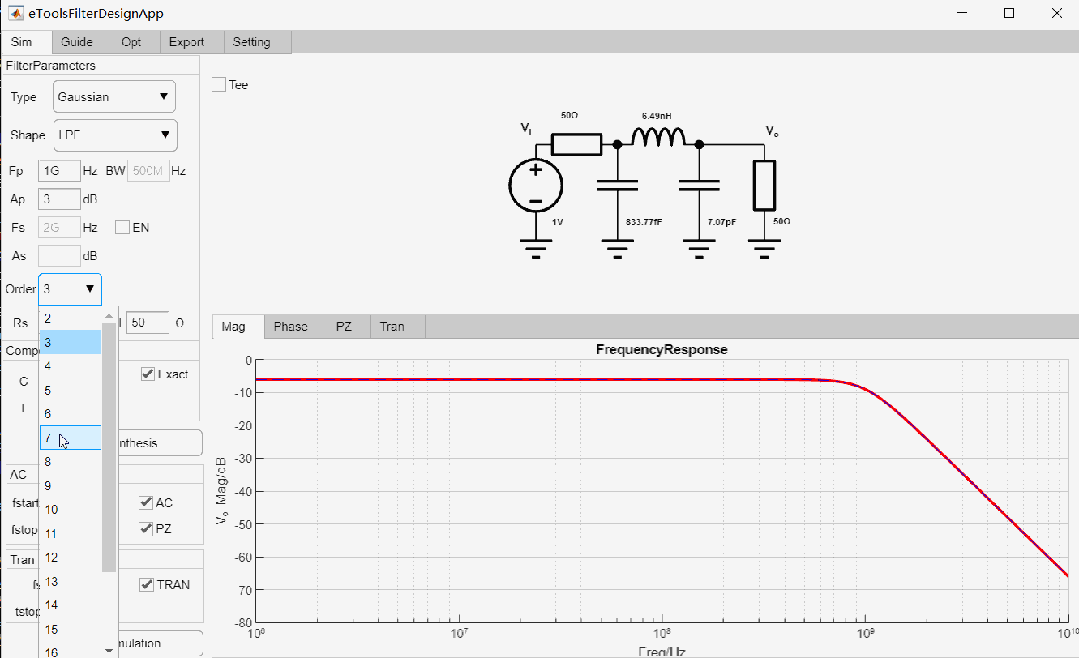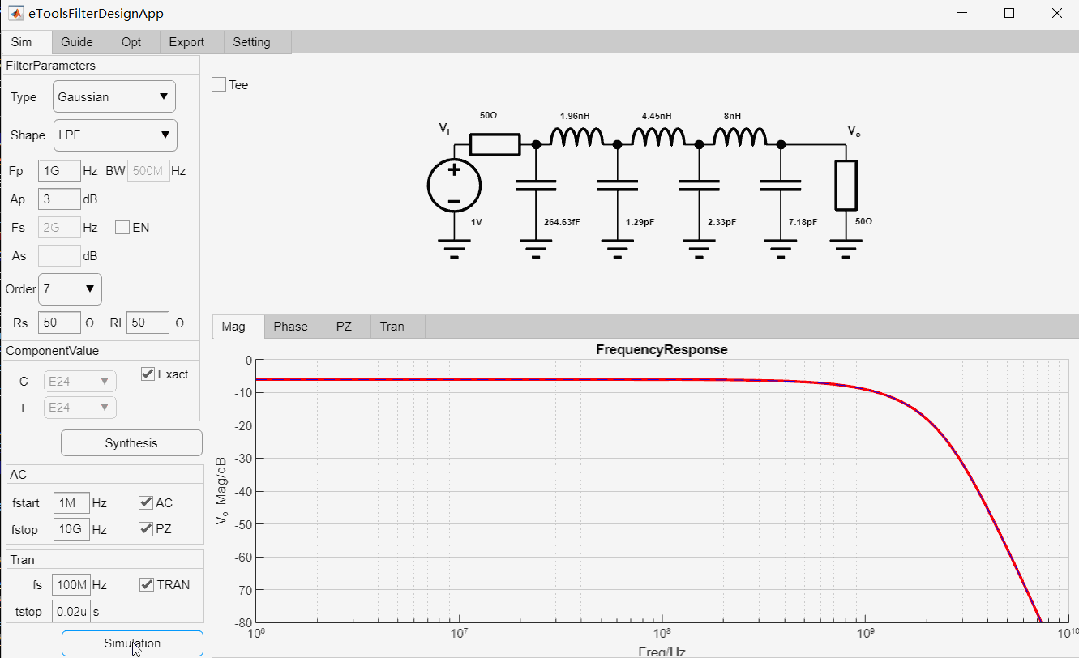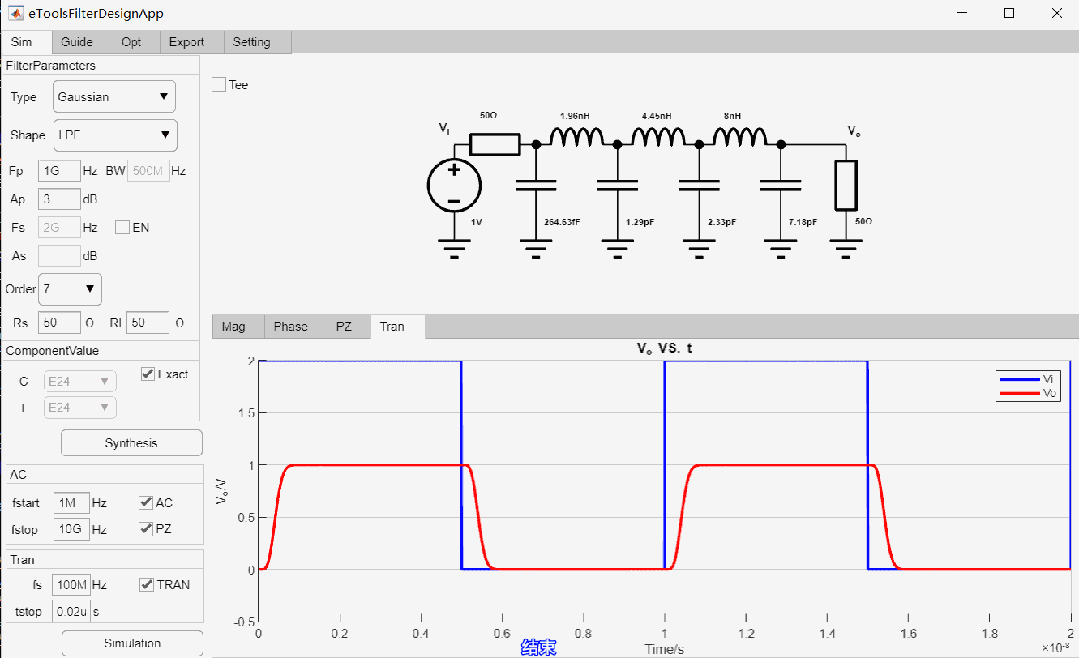
最终设计参数如下：

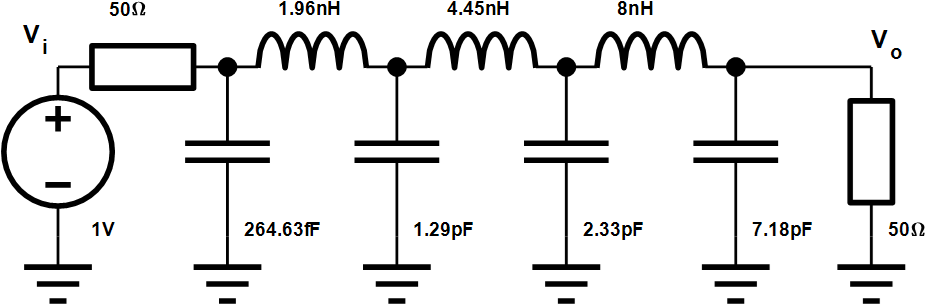
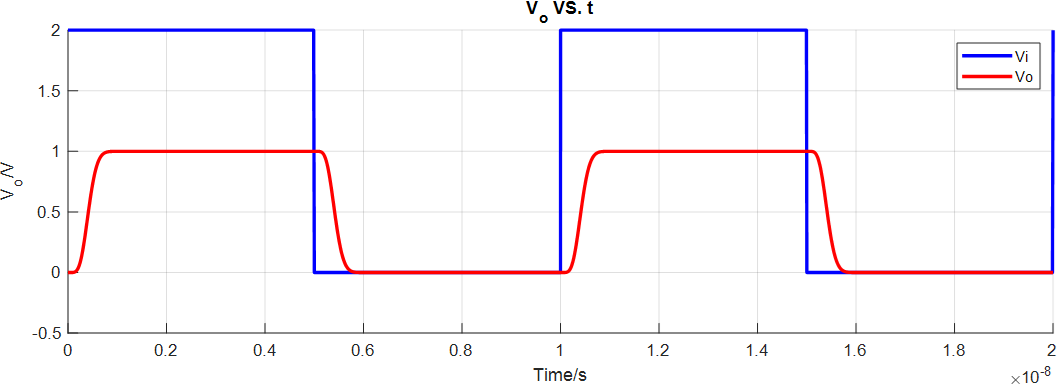
高斯滤波器瞬态仿真结果：

Gaussian BPF设计举例

设计6阶带通Gaussian滤波器, 中心频率为1GHz，带宽为1GHz，50欧姆输入，输出阻抗为高阻，最后进行瞬态仿真，设计过程如下：

最终设计参数如下：

AC仿真结果：

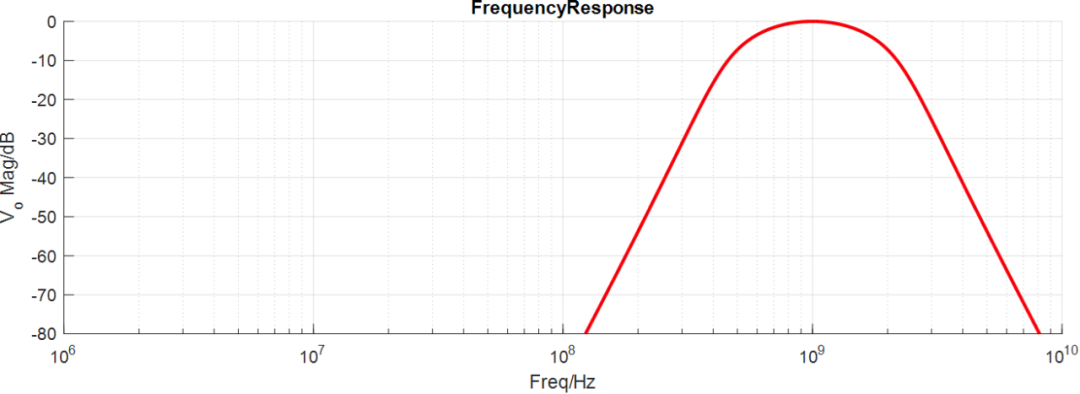
瞬态仿真结果：

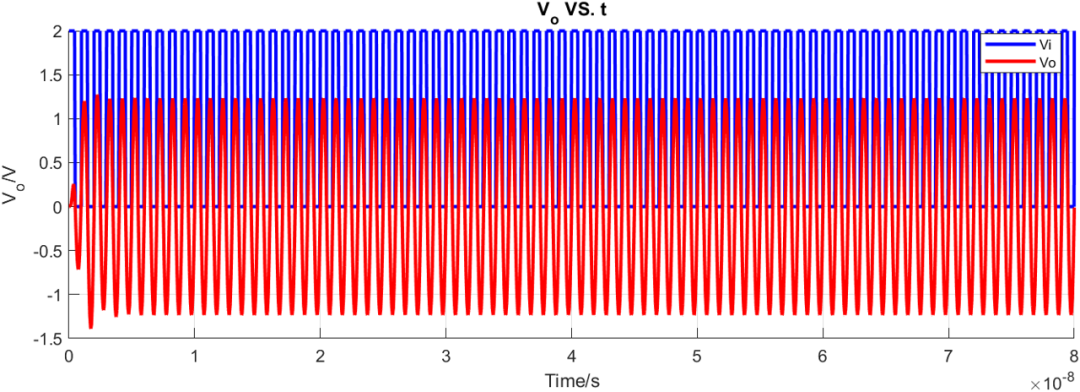
如果将滤波器带宽继续变窄为100MHz：

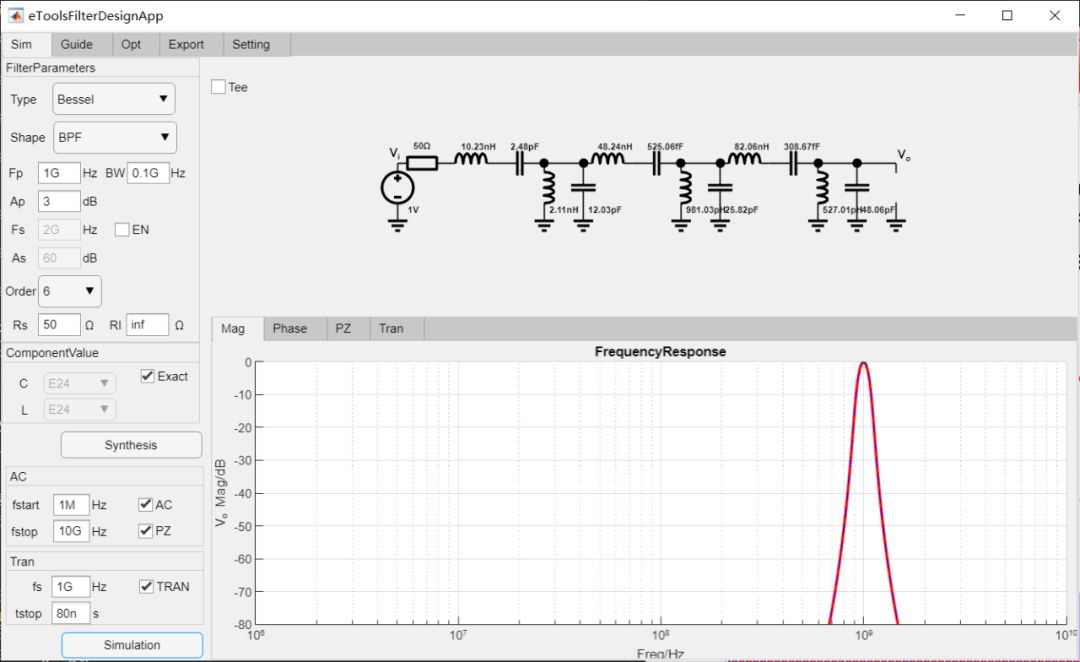
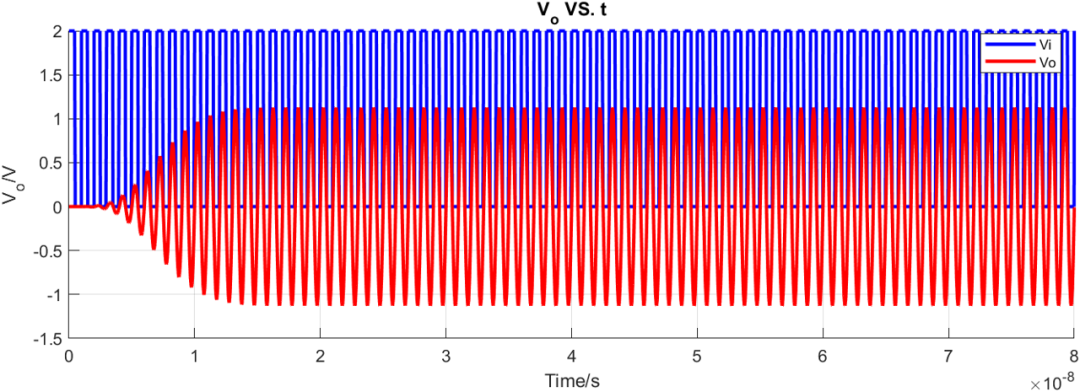
高斯滤波器的瞬态特性：

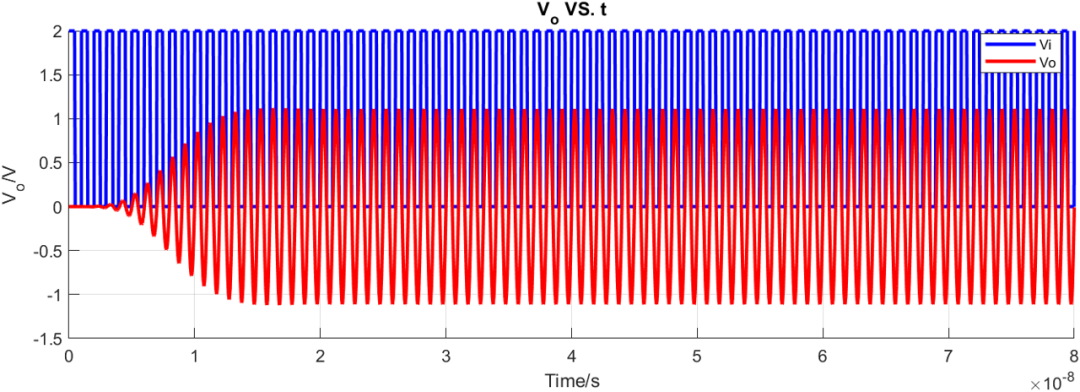
同样参数对比贝塞尔滤波器的瞬态特性：

同样参数对比巴特沃斯瞬态特性:

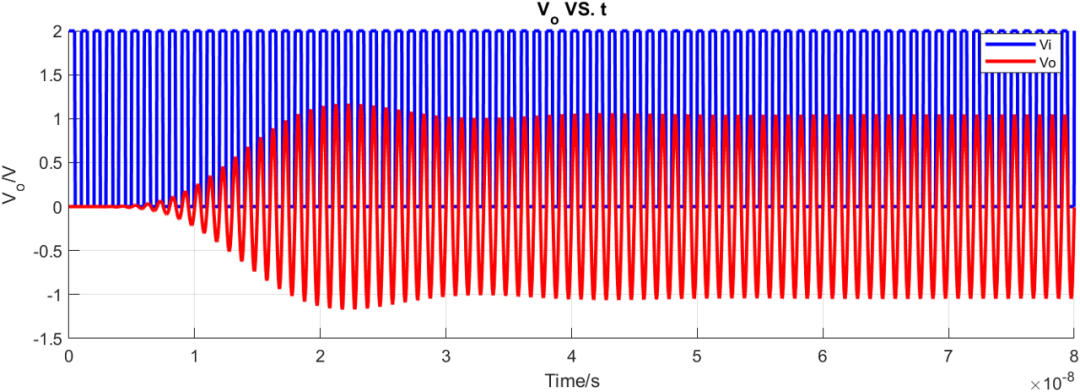
可以看到同样滤波器设置参数下，高斯滤波器具有最小延迟和最小过冲。

程序的Matalb源码已经上传GitHub中(https://github.com/etools361/MatlabGaussianFilterDesignApp)，有兴趣的同学可以下载试用体验，当然也欢迎技术交流。