

HDCP 2.2身份验证:RSA加密
描述
在博客文章 HDCP 2.2 身份验证过程 – 简介中,我们讨论了为什么需要 HDCP,以及 HDCP 身份验证过程的基本步骤。我们注意到,RSA 的高级版本是身份验证和密钥交换期间使用的基础加密标准。
在这里,我们将讨论 RSA 加密的基础知识。
RSA 加密的基础知识
密码学中的所有加密和解密技术可分为两类:
对称密钥
公钥
在对称密钥类别中,发送方和接收方都知道加密密钥和解密密钥,或者在发射机和接收机之间共享通用加密密钥,而解密密钥相同或易于从加密密钥计算。这种类型的加密技术的一个常见示例是 AES,它也用于 HDCP2.2 中用于加密视听内容。
在公钥类别中,加密密钥是公开的和已知的,但是如果没有只有接收者知道的信息,私钥在计算上是不可行的。此类别中最流行的版本是使用公钥技术的 RSA。
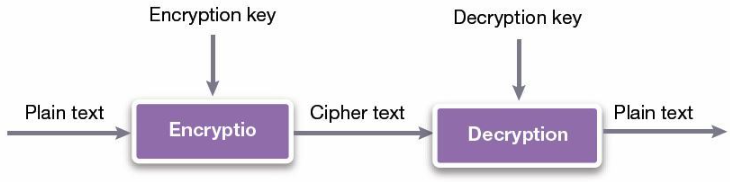
图1:密码学的一般原理
RSA 加密基于由私钥和公钥组成的密钥对。每个接收方都有其私钥和公钥。私钥用于加密和检查签名,而公钥用于加密纯文本。公钥不是秘密的,可以以纯文本形式发送,而私钥是保密的,可以通过极高的计算工作量从公钥派生。
使用公钥和私钥对的RSA加密的优点是,接收器和发射器之间没有相同的密钥。RSA加密的缺点是密码文本和纯文本的计算很复杂。
从数学上解释RSA算法,公钥由一对数字(e,n)和一对数字(d,n)的私钥组成,其中n = p*q,其中p和q是大的秘密素数。图 2 显示了加密,其中纯文本或消息由一个数字 m 表示,该数字上升到公开指定的幂 e,然后在结果除以公开指定的乘积 n(两个大的秘密素数 p 和 q)
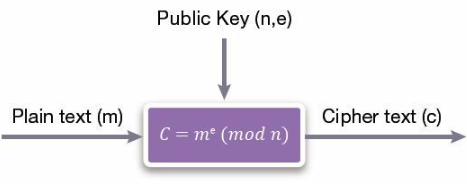
图 2:使用公钥的 RSA 加密
解密也类似,如图 3 所示,只是使用了不同的秘密电源 d,其中 e.d≡1 (mod(p-1)。 (问题-1))。系统的整体安全性部分取决于分解已发布除数 n 的复杂性。
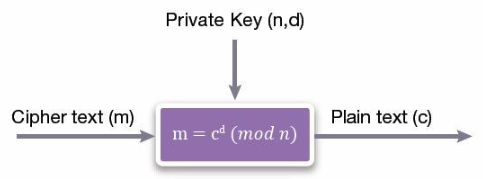
图 3:使用私钥的 RSA 解密
总结算法,如果两个人,说爱丽丝想和鲍勃交流,那么
Bob 选择秘密素数 p 和 q 并计算 n = pq。
Bob 选择 e 与 e, (p − 1)(q − 1) = 1。
Bob 用 de ≡ 1 mod (p − 1)() (q − 1) 计算 d。
Bob 公开 n 和 e 并保持 p、q、d 的秘密。
Alice 将 m 加密为 c ≡me (模组 n)并将 c 发送给鲍勃。
鲍勃通过计算 m ≡ 解密cd(mod n)。
尽管非常困难,但只要有足够的计算能力,普通的RSA仍然可以被打破。这就是为什么 HDCP2.2 使用称为优化非对称加密填充 (RSAES-OAEP) 的普通 RSA 衍生产品的原因,它利用填充和哈希函数。
审核编辑:郭婷
-
使用加密和身份验证来保护UltraScale/UltraScale+ FPGA比特流2023-09-13 576
-
HDCP 2.2:使用中继器进行局部性检查、SKE和身份验证2023-05-29 3396
-
PN5180无法使用mifare classic进行身份验证怎么解决?2023-03-23 642
-
是否有支持WSS + websockets身份验证的库?2023-02-23 496
-
使用关联数据探索经过身份验证的加密2023-02-07 1559
-
PCB身份验证器2022-07-22 592
-
身份验证和生物识别身份系统应用越加广泛2019-02-27 1762
-
Vivado和SDK身份验证错误2019-01-02 8343
-
无线身份验证的门禁控制系统设计方案2018-11-05 1755
-
ATECC508A加密引擎身份验证器件的详细中文数据手册2018-07-02 2501
-
什么是身份验证和授权2010-04-03 5998
全部0条评论

快来发表一下你的评论吧 !

