矢量调制分析基础知识（下）

VSA 数字调制分析概念和工作原理

VSA 可被看作是基于软件的测量接收机。它实际上是在数字调制解码时采用与大多数数字无线接收机相似技术的 I-Q 接收机。不同的是，VSA 软件专为高精度参数测量和调制特性显示而设计。还有，VSA 是能够测量和分析数字通信发射机与接收机系统几乎所有方面的测量工具。

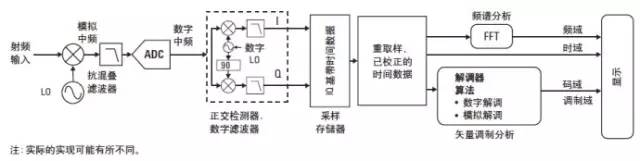
图 7. 带有射频前端的 VSA 测量系统的简化方框图。对于其它前端，VSA 软件将执行所给前

端不支持的功能。

图7 显示了 Agilent 89600B VSA 的简化系统方框图。你可能注意到系统方框中的许多部分与图6 所示的数字通信接收机的类似。通过几个阶段的超外差式混频将射频输入信号下变频为能被 ADC 精确数字化的中频信号。有多种不同类型的前端都可完成这个过程。有的比如信号分析仪提供射频信号检测和中频数字化。其它的像示波器和逻辑分析仪则提供完全数字化的基带信号。 VSA 所需的输入是经过数字化的时间采样数据。随后，对这个数字化信号进行矢量 ( 正交 ) 检测和数字过滤 ; 如果需要，将其最后一次下变频为 I 和 Q 基带信号格式 (I-Q 时间数据 ) 并存储在 RAM 中。接着就是使用 DSP 算法解调这个信号 ; 恢复载波和符号时钟并应用建滤波和解码 ( 恢复原始比特 )。几乎任何一种调制格式都可被这个 DSP 软件解调。

VSA 的实现与无线接收机不同，VSA 处理采样的信号是基于样本块 ; 而无线接收机是实时串行串行数据。当为 VSA 软件提供无线接收机参数时，它可以通过 DSP 的处理过程合成这个接收机。它能够提供接收机的全部功能，甚至包括生成模拟波形。因为信号实际上是数字化的，它可被后期处理并在时域、频域或调制域的任何域中查看。

VSA 数字解调

VSA 中数字解调过程的核心是数字解调。图8 显示了 Agilent 89600B 所使用的数字解调算法的简化方框图。数字解调算法提供通用解调，仅需输入信号很少的先验信息即可执行解调，并适用于非常广泛的调制格式。解调器提供载波锁定、符号时钟恢复和比特恢复 ( 对实际已编码的 1 和 0 进行解码 )，并生成 I-Q 测量波形。解调器还能产生理想的 I-Q 波形，这些波形由真实的已恢复比特 ( 称为 I-Q 参考波形 ) 合成。I-Q 测量波形与参考波形的差可得到 I-Q 误差波形。分析 I-Q 误差波形可得出调制质量数据结果，该结果可以通过各种

数据格式和显示输出进行查看。

解调过程从配置 VSA 基于软件的解调器开始。解调算法必须根据特定的数字调制格式进行配置，以恰当地解调和分析信号。大多数分析选件提供一组标准预设值，例如 GSM、W-CDMA、cdma2000 或 802.11a/b/g，可自动配置解调器。在这些情况下，输入中心频率并选择一个标准预置，软件就可以解调信号。

灵活配制或用户定义的解调

Agilent 89600B VSA 软件通过一个通用的、用户可定义的解调器提供更多额外功能。它允许针对非标准格式或故障诊断定制解调器配置。图8 的解调方框图显示了内部解调过程 ( 矩形框内 ) 和用户可设的配置参数 ( 椭圆或圆角矩形框内 )。椭圆框内的项目是用于定义测量所需的解调器的配置参数。圆角框内是用户可调节的输入参数。解调算法至少知道调制格式 (QPSK、FSK 等 )、符号速率、基带滤波器类型和滤波器 α/BT 等参数。这组参数通常通常足以满足解调器锁定信号以及很多格式的符号恢复的需要。其它格式，像定制的 OFDM 针对具体格式类型则需要额外的信息。

图 8. 数字方框图

数字解调基带滤波

前面提到，数字解调利用基带滤波来限制带宽和降低码间干扰。还有，就像通信接收机一样，数字解调基带滤波必须配置的与被测系统匹配，以精确地解调信号。这同样要求滤波器类型 ( 如 Nyquist 或 Gaussian) 与滤波器带宽系数 (α 或 BT) 匹配。

如图9 所示， I-Q 测量波形和 I-Q 参考波形具备独自的信号处理路径和基带滤波。I-Q 测量波形必须使用与被测系统的接收机滤波相匹配的基带滤波。该滤波器称为测量滤波器或 Meas Filter。I-Q 参考波形必须使用与被测系统的总体 ( 发射机和接收机 ) 信道滤波相匹配的基带滤波。该滤波器称为参考滤波器或 Ref Filter。参考滤波器能够仿真总体信道滤波因为它用来合成可被“完美的”线性信道信道响应接收的理想的 I-Q 信号。解调器必须利用总体系统信道滤波才能精确地合成参考 I-Q 波形。

选择恰当的滤波

在数字通信系统中，基带滤波可能出现在发射机或接收机上 ; 或者分布在发射机和接收机之间，发射机中完成一半滤波，接收机中完成另外一半。这是个很重要的概念，会影响到解调器在处理 I-Q 测量波形和 I-Q 参考波形时所需的滤波器类型。VSA 软件的 Meas Filter 代表系统接收机的基带滤波，而Ref Filter 代表整个系统的基带滤波 ( 接收机和发射机整体的信道滤波 )。

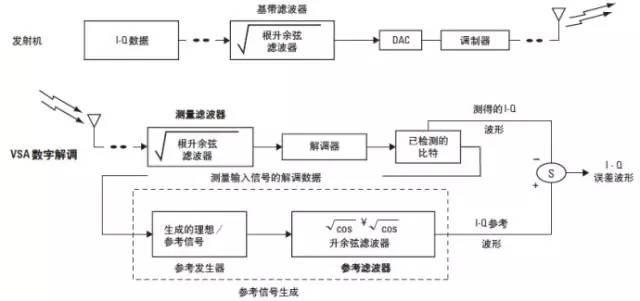
图 9. 可选的匹配滤波器用于代表发射机和接收机的滤波。

借助已检测的比特，再结合对调制类型和滤波的了解，可以确定理想信号。

选择正确的解调基带滤波可能并不像想象中的那么简单直接，尤其是对于分布式系统。例如，北美数字蜂窝 (NADC) 标准采用分布式滤波 ; 在发射机和接收机中都使用了根升余弦滤波器。参见图 9。在 VSA 解调里，针对 I-Q 测量波形使用一个根升余弦滤波器 ( 与系统接收机滤波匹配，系统发射机含有一个类似滤波器 )。对于 I-Q 参考波形，您可以使用一个升余弦滤波器 ( 与整体系统信道滤波匹配 )。这是因为平方根 ( 升余弦 ) 乘以平方根 ( 升余弦 ) 的结果就等于升余弦滤波器。

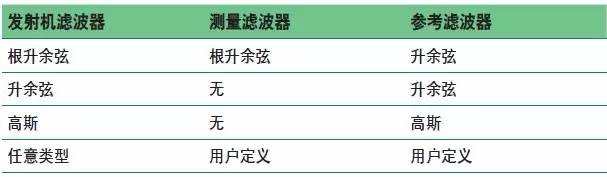
表1 显示了一些常用的滤波器类型以及测量和参考滤波器基于发射机滤波器类型的选择示例。

表 1. 常用的发射机滤波器类型

滤波器 α 和 BT 带宽时间产品

可精确代表被测系统的另一个滤波器参数是滤波器带宽系数，定意为滤波器 α 或 BT。每个滤波器类型将会有一个对应的滤波器带宽系数 ; Nyquist 滤波器使用 α，高斯滤波器使用 BT。解调器对测量滤波器和参考滤波器使用相同的 α 或 BT 值。

根据具体的应用需求，数字通信使用许多滤波器类型，传统上，使用Nyquist ( 升余弦 ) 滤波器是因为它能最小化 ISI 。如图10 所示，Nyquist 滤波器脉冲响应的峰值幅度出现在符号时刻 t = 0 幅度时，而在所有其它符号时刻为零。也就是说，该响应在符号周期的整数倍 (1 除以 ƒs) 通过零点。这意味着 Nyquist 已过滤的符号不会干扰周围的符号 ( 即符号间干扰为零 )。虽然Nyquist 滤波器可最大限度地减少 ISI，但对于有些应用 ISI 并不是最重要的标准。另外两种常用的滤波器类型是高斯滤波器和 Chebyshev 滤波器。高斯滤波器不具备最佳的 ISI 特性，但在平衡载波功率、占用带宽和符号时钟恢复方面具有优势。它通常使用在 GSM ( 全球移动通信系统 ) 的无线电话系统中。Chebyshev 滤波器具有陡降特性，能够有效减少对相邻信道的功率泄漏。

Chebyshev 滤波器通常应用在使用 CDMA ( 码分多址 ) 调制方案的无线电话系统中，例如 cdmaOne 和cdma2000。除了这里探讨的类型外，数字通信领域还采用许多其它类型的滤波器。

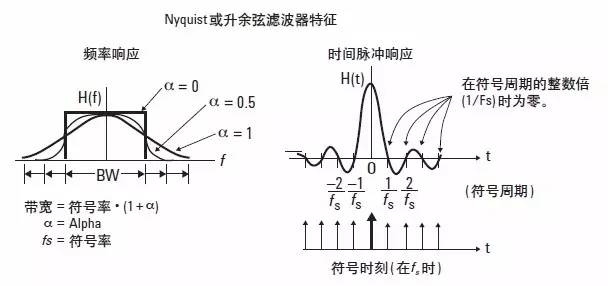
图 10. Nyquist 滤波器最大限度地降低符号间干扰 (ISI)。

Alpha

Alpha (α) 描述了 Nyquist ( 升余弦 ) 滤波器的滚降程度。参见图 10。Alpha也称为滚降或多余带宽因子。α 值较高，则会增加理论最小值之外的带宽。调制原理指出，发射一个信号所需的最小带宽等于符号率的一半。不过，要实现这个系统带宽，需要一个完美的砖墙式 ( 矩形 ) 滤波器，也就是 α 等于 0，占用带宽等于符号率。但砖墙式滤波器并不能实现，所以实际中的通信系统一般采用 α 等于 0.3 的滤波器。α 值为 0.3 意味着滤波器将使用比理论最小值多 30% 的占用带宽。这个值是频谱效率和最小 ISI 的一个很好的折衷。对于给定 α 的占用带宽近似等于采样率乘以 (1 + α)。

BT — 带宽时间产品

BT ( 带宽时间产品 ) 是高斯滤波器对应的滤波器系数，描述了这个滤波器的滚降程度。高斯滤波器通常使用 0.3 ~ 0.5 的 BT 值。

解调分析

一旦用户提供了输入配置，解调器就利用它们并通过 DSP 以块状格式接收来自 VSA 可用样本存储器的 I-Q 时间数据。VSA 软件能够接收来自外部硬件 ( 例如 Agilent X 系列信号分析仪或 Infiniium 系列示波器 ) 或记录文件的I-Q 时间数据。解调器使用所提供的中心频率和符号率锁定载波，并且从调制载波上恢复符号时钟。注意，解调器参考时钟不需要与源时钟锁定。解调算法自动提供载波和符号锁定 ; 不必提供额外的源时钟输入。然后信号通过补偿过程应用增益和相位校正。补偿数据 ( 例如幅度幅度偏差和 I-Q 偏置误差数据 ) 被存储并可以在误差汇总表中查看。随后，应用数字基带滤波以恢复基带 I-Q 波形 (I-Q 测量时间数据 )。将已恢复的 I-Q 波形送入到符号检测器，基于具体的调制格式来尝试确定发射的符号。从符号块中，解码和恢复串行数据比特 (1 和 0)。参考产生器使用已检测的符号再结合调制格式、符号率以及特定滤波，从而合成一组理想的 I-Q 参考基带波形 (I-Q 参考时间数据 )。最终将测得的 I/Q 波形和参考 I-Q 波形进行对比，得到一系列误差特性 ( 与理想波形之间的偏差 )，例如相位误差、幅度误差和误差矢量幅度(EVM)。

I-Q 测量和 I-Q 参考信号

通过对比测得的信号与理想的参考信号，可以分析 I-Q 调制信号的质量。参见图 9。解调过程会生成两个波形 : I-Q 测量波形和 I-Q 参考波形。 I-Q 测量波形是针对输入信号解调的基带 I-Q 数据，也称为 IQ 测量时间。I-Q 参考波形是如果输入信号是理想的 ( 没有误差 )，在解调该输入信号后应该得到的基带 I-Q 数据，也称为 IQ 参考时间。假设原始的数据序列可以被恢复， I-Q 参考波形从 I-Q 波形恢复的数据比特中采用数学方法导出。I-Q 参考波形的产生开始于恢复已解调 I-Q 测量波形的实际符号比特，随后重建理想的 I 和 Q 状态序列。这些状态再作为理想的脉冲，并根据参考信道滤波进行基带过滤，从而生成一个理想的 I-Q 参考波形。然后对比 I-Q 测量波形与 I-Q 参考波形，分析输入信号的质量。从已测波形中减去参考波形得到误差矢量波形，或 I-Q 误差波形。这种方法能够揭示非常微小的信号变化，并能转化为信号的质量信息，这些信息是传统调制质量测量方法所不能提供的。

测量概念

现在已解释了一些数字调制基础和 VSA 的系统原理，下一步是了解关于数字调制分析测量结果与用于系统故障诊断的轨迹轨迹显示。下面的例子显示了 QPSK ( 正交相移键控 ) 的测量结果，调制信号的符号速率是 50 ksym/s， α 等于 0.35 的根升余弦基带滤波器。正交表示载波信号在相差 90°的相位状态之间转换。信号以 90° 为增量在 45° 到 135°、-45° 或 -135° 变化。QPSK 有四个可用状态。每个状态分配一个 0 ~ 3 的二进制值，这要求每个状态有 2 个比特，也就是每符号两个比特。只要两个 I 值和两个 Q 值就可生成四种状态，同时满足双比特码元的要求。

矢量 ( 或 IQ) 图

矢量示意图，通常更多地称为数字调制的 IQ 图，显示了时间上各个时刻所恢复的复杂 I-Q 基带信号。它显示了信号状态以及信号在符号之间移动时的跳变过程。从原点到矢量示意图上某个点绘制的矢量线对应着此刻的瞬时电压。

图 11a 显示了前面提到的 QPSK 调制信号的 IQ 图示例。IQ 图显示了 4 个理想的状态位置 ( 以十字表示 )，分别是 45°、135°、-45° 和 -135°。还有已检测的符号和符号间的跳变。IQ 图给出了峰均电压比，它可用于确定放大器的压缩情况。

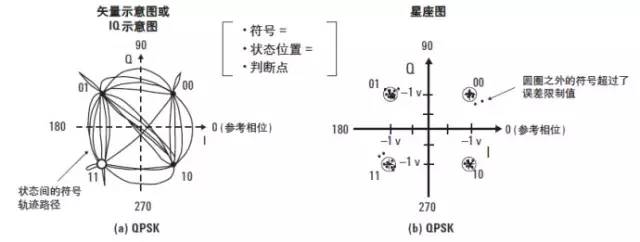
图 11. QPSK 量图和星座图

矢量图解释

在 I-Q 平面上查看信号时，记住你是在观察信号相对载波的幅度和相位。未调制的载波是相位参考 (0°)。图11 中，每个检测的符号都是相对未调制载波以不同的幅度和相位进行调制，但频率与载波一致。如果检测到符号频率与未调制载波的不同，它的表象是信号相对未调制载波连续增加或减小相位似的移动。还有，数字调制属于三维测量，根据 I ( 同相)/Q ( 正交)分量与时间的关系进行调制。而 IQ 图仅是二维图，所以与 I-Q 平面 ( 或 CRT屏幕 ) 垂直的时间参数无法显示。

星座图

图 11b 显示了与前面相同的 QPSK 信号的星座图。星座图显示了与符号时钟同步的载波幅度和相位。这些测量点通常就是检测判断点，代表已检测的符号。它与 I-Q 图类似，只是不显示状态间的跳变轨迹轨迹。

理想状态下，所有符号都应显示为单点，并集中在理想状态位置处 ( 以十字坐标显示 )。理想状态是指信号没有误差时的符号位置。不过由于信号的损伤及其它调制误差会造成偏差，符号会分散在理想状态位置的周围。

89600B VSA 允许你在理想状态周围放置一个定义好的误差限制圈。显示的实际已检测符号与理想状态可以帮助您直观地了解信号质量。星座图有助于识别幅度不平衡、正交误差或相位噪声等信号损伤。

误差矢量幅度 (EVM)

在数字通信系统中应用最为广泛的调制质量指标是误差矢量幅度(EVM)。误差矢量是指在给定时间的理想参考信号和所测信号之间的矢量差。参见图 12。误差矢量是一个复参量，包含幅度和相位分量。不要将误差矢

量幅度与幅度误差、误差矢量相位与相位误差相混淆。

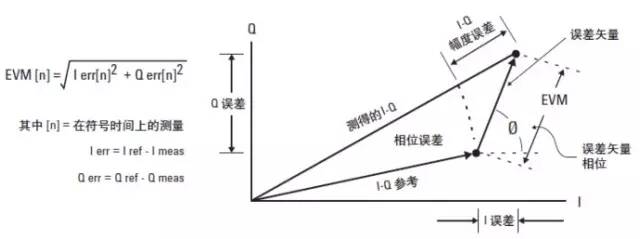
图 12. 误差矢量幅度 (EVM); 实际测得的信号与理想参考信号的差异

EVM 定义为在符号时钟跳变时刻误差矢量的均方根 (rms)。按照惯例EVM 通常归一化为最外面符号的幅度或符号平均功率的平方根。EVM 测量在有些通信标准中也称为相对星座误差 (RCE)，各种相关数据结果对于任意

数字调制格式中影响信号的幅度和相位轨轨迹路的损伤都十分敏感。因此，EVM 是一种分析诊断通信系统基带、中频或射频部分中的故障的理想测量工具。

图13 是图12 中定义的调制质量测量的示例。误差矢量时间数据 ( 轨迹A) 是根据 I-Q 测量信号和 I-Q 参考信号上相应符号点计算出的误差矢量幅度。误差矢量频谱数据 ( 轨迹 B) 显示了误差矢量时间数据的频谱。也就是说，误差矢量时间数据被加窗并FFT 以生成误差矢量频谱轨迹。这种格式能够揭示使得制载波偏离理想路径的多余信号的频谱成分。如果这些误差成分是确定的，它们会以频谱轨迹的形式显示在误差矢量频谱上。测量这些频谱，可以更深入地了解这些误差信号的本质与来源。频率峰值通常会对应方框图中某处的一个信号。I-Q 幅度误差 ( 轨迹 C) 和 I-Q 相位误差 ( 显示 D) 显示了 I-Q 测量信号和 I-Q 参考信号间的误差。I-Q 幅度误差显示幅度误差，I-Q相位误差显示相位误差。

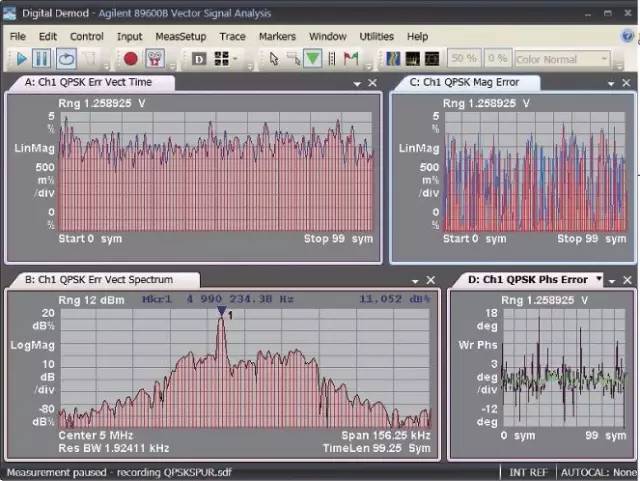图 13. 轨迹 A ( 误差矢量时间 ) 显示了符号点处的误差矢量幅度。轨迹 B ( 误差矢量频谱 ) 显示

了误差矢量时间数据的频谱。轨迹 C (IQ 幅度误差 ) 是测量 IQ 波形和 IQ 参考波形的幅度差。

轨迹 D (IQ 相位误差 ) 是测量 IQ 波形和 IQ 参考波形的相位差。

符号表 / 误差汇总

符号表 / 误差汇总测量结果可能是数字解调最强大的工具了。你可以看到解调比特，以及所有解调符号的误差统计。例如，查看 rms EVM 值可以帮助你快速评估调制精度。还有其它很多有价值的误差报告。图14 显示了前面使用的 QPSK 信号的符号表 / 误差汇总数据。标记读数显示的是符号表中突出显示的比特对应的值，代表符号 3，数值为 2 (“10”的二进制值 )。可以看出这个值与 QPSK 调制所需的双比特码元一致。误差表显示了适用于 QPSK 调制信号的统计数据与误差数据。其它误差值为其它格式所用。我们已经讨论了一些基本的调制测量，但还有很多定性显示和定量测量并未涉及。

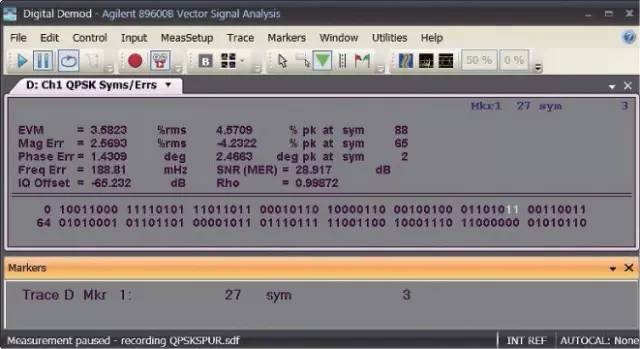图 14. 符号表 / 误差汇总数据提供解调比特及所有已解调信息的误差统计。

模拟调制分析

矢量调制分析可以提供的另一种重要的测量工具是模拟调制分析。模拟调制产生 AM、FM 和 PM 解调结果，类似于调制分析的输出，允许你查看幅度、频率和相位特性对时间的关系。这些模拟调制分析能力增强了 VSA 已有的数字调制分析功能，提供完整的分析数字通信系统的测量解决方案。例如，可使用模拟调制能力分析像 FSK ( 频移键控 ) 这样的有意调制 ; 像相位噪声或AM-PM 转换这样的无意调制 ; 或者像频率或相位稳定或脉冲成形过程这种单脉冲信号参数。

解调信号的过程看上去挺复杂，但矢量调制和 I-Q 调制过程的基础特性使得解调变得简单。前面提到的矢量或 IQ 图 ( 图2 和 11) 显示了调制载波相对未调制载波的瞬时幅度和相位，这有助于显示数字调制特性。不过它还提供了一个简单的方法来查看模拟调制信号特性，例如图15 所示的 AM、PM 和 FM 调制。未调制连续波 (CW) 信号简单地显示为一个幅度与相位恒定的固定点。AM 信号的轨迹经过原点沿着固定线路，只有信号幅度发生改变。FM 信号的轨迹是以原点为中心的圆圈，瞬时频率偏差由相位变化率给出。PM 与 FM 的轨迹类似，当然，相位的相对变化是关键参数。在矢量调制中，幅度和相位可同时改变，矢量轨迹会在幅度和相位上都发生变化。

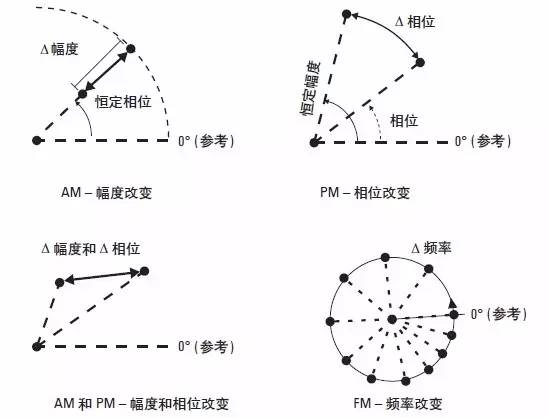图 15. I-Q 示意图中 I-Q 平面上的模拟调制特性。

传统上，为了查看载波调制波形 ( 调制包络 )，应当通过检波移除载波并将结果波形显示在幅度对时间的示波器上。不过，取代在载波上检测调制的思想，在矢量调制中，我们将载波“搬移”或“下变频”到 0 Hz 之后再在剩下的部分里查看调制。频移的直观图将显示利用基本三角恒等式载波上幅度和相位变化是如何被“检测”的。

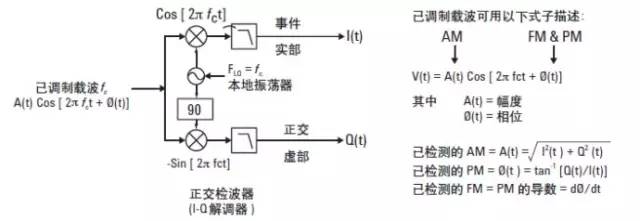
图 16. 调制通过搬移载波频率 (fc) 至 0 Hz 测量。当数字 LO 频率等于调制载波频率时，正交检

波器的输出 — I(t) 和 Q(t) 时域波形 — 就是载波上的调制。

如图16 所示，复调制载波信号以 (V(t) = A(t)Cos[2πfct + Ø(t)]) 表示，频率fc 是用于频率转换的正交混频器 ( 或正交检测器) 的输入。为恢复基带调制信号，首先通过设置 LO 频率为 fc 将载波下变频至基带 (0 Hz)。随后基带信号经过低通滤波，只留下差频。这个过程生成实部 I(t) 和虚部 Q(t) 时域波形，表示

已调制载波信号与未调制 LO 信号的幅度和相位差，以载波为参考。这是载波调制以 I(t) 和 Q(t) 分量 ( 直角坐标 ) 表示的形式，而不是幅度 A(t) 和相位 Ø(t)。前面提到 I-Q 解调执行极坐标—直角坐标的转换。不过，通过对 I(t) 和 Q(t) 分量应用一些运算和简单的三角恒等式，我们也能够获得瞬时幅度 A(t) 或相位

Ø(t) 这些载波上的变化。这就是 AM 和 PM 调制。

幅度调制 AM 是载波幅度 A(t) 随时间的变化，由 I(t) 和 Q(t) 的平方和开平方根得出。

AM = A(t) = sqrt[I2(t) + Q2(t)]

相位调制 PM 是相位 Ø(t) 随时间的变化，等于 [Q(t)/I(t)] 的反正切。频率调制 FM 是相移对时间 dØ/dt 的导数。即，FM 是 PM 的导数:

PM = Ø(t) = arctan[Q(t)/I(t)]

FM = PM 的导数 = (dØ/dt)

从 I(t) 和 Q(t) 开始，通过应用基本三角恒等式，我们完成了载波的第一阶解调，能够查看 AM、PM 和 FM 调制。实际中，VSA 软件使用精密的解调算法再结合频率和相位误差校准程序，可以精确地将有意和无意调制从载波上分离出来。模拟解调可使 PM、FM 与 AM 完全分离。同样地，AM 也可与 PM、FM 完全分离。

总结

本文介绍了运用在基于软件的矢量信号分析中的矢量 / 数字调制技术和数字调制分析的基本原理。描述了数字 ( 矢量或 I-Q) 调制和常见数字调制格式。VSA 架构类似于数字通信系统，因此我们也描述了无线接收机和发射机的方框图，介绍了生成、发射、接收以及恢复原始数字信息的过程。随后，我们着眼于 VSA 数字解调方框图并描述了每个功能及正确解调信号并进行测量的相关解调参数。带有矢量调制分析功能的 VSA 提供强大的专业测量能力，允许你贯穿整个数字系统 ( 系统使用 I 和 Q 信号 ) 的方框图进行表征和故障诊断。通过借鉴本章节内容，针对你的通信系统，你将更加明确地选择所需的测量仪器和必备工具。现在，VSA 既可作为嵌入式专用软件运行在信号分析仪，示波器和逻辑分析仪上，也可作为独立软件与多种测量前端和仿真软件兼容。