电平设计基础1：逻辑门电路高速特性（1）

一，逻辑门电路

我们在设计数字电路时，都希望器件的功耗低、速度快并且封装（器件价格）便宜。但这如同所有的“神秘三角”一样，是不可兼得的。所有的逻辑器件都是在权衡了功耗、速度和封装之后的折衷方案：

——“神秘三角”有项目的管理三角：范围、时间和成本；病毒三角：传染性、毒性和适应性（新冠病毒之所以没有灭绝人类，就是因为它受到了这“神秘三角”的约束）；等。

1. 标准封装在制造时节省了费用，但降低了器件的灵活性；
2. 标准封装限制了每个封装单元内的门电路和管脚数量，迫使设计者将大的系统拆分成多个器件；

——器件之间的信号连接响应明显比同一封装内信号要慢，所需的功率更大；即，使得系统的性能降低，功耗增加。

3. 标准的封装结构限定了器件所允许的最大散热能力，如果要改进封装的散热能力，则需要花费额外的成本；
4. 随着芯片制造工艺的改进，每个逻辑单元尺寸变的更小，在相同的封装内可以集成更多的门电路数量；高密度的封装有助于降低产品尺寸和组装成本，但这意味着需要更大的单位面积散热的能力；

——每个封装所允许的最大散热功耗限定了封装内的门电路数量。

5. 高速器件通常消耗更大的功率，速度和功率在一定程度上可以相互对应；所以封装的最大散热功耗，也称为了高速的限制因素。

——在相同制造工艺下，速度越高的器件功耗会越大。

所以对于逻辑门电路高速特性，我们主要考虑如下三个方面：

1. 功耗：分为静态功耗和 动态功耗 ；
2. 速度：

1, 理论上：数字逻辑的设计重点是关注 逻辑门电路的传输延时 ；

2, 实际上：通常取决于 最小输出转换时间（边沿时间） 。

——较快的转换时间会导致回流，串扰和振铃等与传输延时无关的问题倍增。

3. 封装，对于任何高速器件封装都会引入：管脚寄生电感、寄生电容以及散热的问题。

二，功耗

我们想要知道一个逻辑器件的功耗，一般会查看其数据手册上的典型电流值Icc，但这并非是器件的实际功耗，或则说在一些条件下器件的功耗会远大于标称的Icc电流值。举个栗子：常用的16位驱动器74LVTH16245，如果16个输出管脚同时快速翻转，那么其实际功耗应该会远超规格书中的Icc，如下图所示。

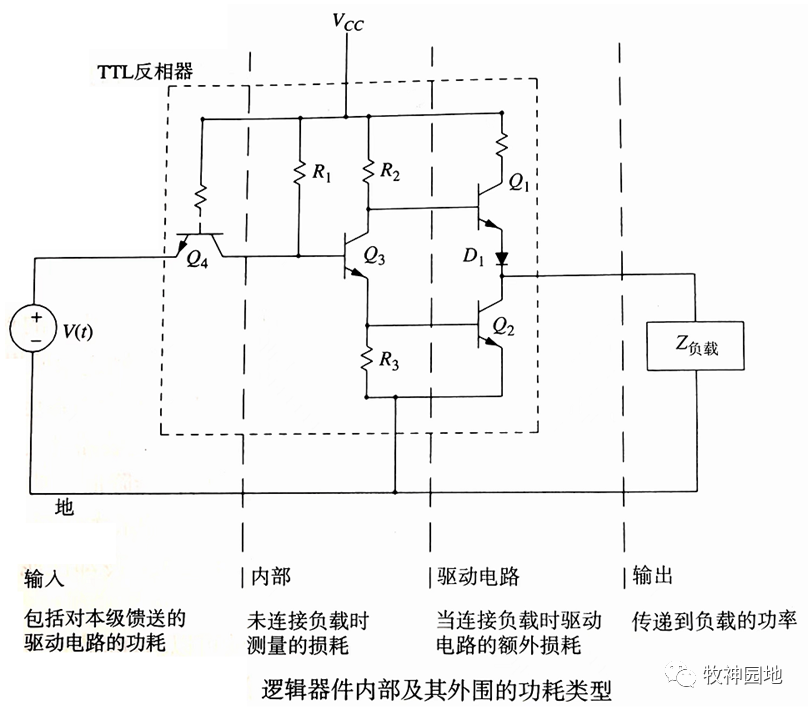
如下图所示，为一个简单的TTL反相器的内部逻辑结构，从功耗角度分为4部分：

——如下每一种功耗都可以进一步细分为：静态功耗和动态功耗。

1. 输入功耗；
2. 内部功耗；
3. 驱动电路功耗；
4. 输出功耗。

1，静态功耗和动态功耗

这里非常重要的概念是：静态功耗和动态功耗。我们所有的功耗都可以将它分为这两部分。

静态功耗：指逻辑电路保持一个逻辑状态时消耗的功率。静态功耗可以由每个阻性单元两端电压V和电流I的乘积计算所得（P静态 = V*I），并且求和得到总功率，这是在没有负载情况下的静态功耗（即数据手册上看到的Icc标称值）。

——需要强调的是：静态功耗是不计负载损耗的器件自身功耗。

但实际上逻辑电路不跳变则无法传递信息，也就成了无用之物，我们需要器件“动”起来，那么器件就要消耗超过它正常静态功耗之外的“额外功率”。当这个变化很有节奏时，举个栗子：以时钟信号频率跳变；那么：动态功耗 = 周期频率* 每个周期额外的功率。

——动态损耗最常见的原因：负载电容（RC充电）和偏置电流。

如下图所示为驱动一个容性负载时的情形：

1. t1时刻电路开关A闭合（B断开）：负载电容充电至Vcc，在电容充电时电流流过驱动电阻“R充电”，有功率消耗；
2. t2时刻电路开关B闭合（A断开）：负载电容通过电阻“R放电”进行放电，电流流过驱动电阻，也有功率消耗；
3. t1和t2之间有一个“死区时间”（A和B都断开）：此死区时间是为了防止电源Vcc直接通过开关短路到GND，造成器件损耗增加，甚至烧坏内部开关。

——该“死区时间”的原理同开关电源，在逻辑门电路中，其主要影响器件的功耗和电平切换速率（I/O管脚支持的最大速率）。

那么一个电压源通过电阻R对容性负载C充电或放电时，是如何计算它的功耗呢？

1. 胖友们已经知道电容是一个储能元件，并不会耗电，所以在容性负载充放电过程中不会耗电；

——如果有胖友还对这个问题有疑问：电容器有ESR，有寄生电阻呀等等；建议再回顾《阻容感基础01》中的内容，另外我想说的是：我们要区分电容与电容器这两个概念；电容是指容性，而电容器是指具体的器件，对于容性本身来说，它是不会造成电能的损耗，而造成损耗的是阻性。

2. 我们来考虑RC充/放电电路中电阻R的能量消耗，有如下两个计算方法：

1, 直接计算电阻R在充电RC充电电路中的功耗：P = I² * R，由于电流并非线性的，而是指数函数：(U/R)*exp(-t/τ)；所以需要用到积分公式来进行计算，具体计算如下：

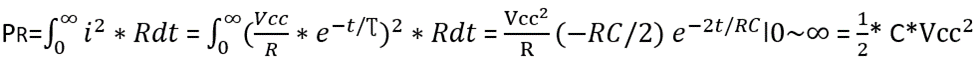
RC放电电路是充电的反向过程，同理其消耗在电阻R上的功耗也为(1/2)* CV²cc；所以充放电的总功耗为：P = CV²cc；

——指数函数的积分（面积）是1（即指数函数积分从-至x的积分值就是其本身，t 是-∞至0，那么可得积分为e⁰= 1），具体请参考《传递函数和波特图》的“说在开头”章节关于自然常数e的描述。

2, 将RC电路看成一个整体，同时将充电和放电看成一个整体；那么器件给R/C充电的总能量，就等于RC充电和RC放电两个过程中总共消耗的能量；电源消耗总能量：P = VccIt = VccQ = Vcc Vcc C = C V²cc；

——电源总能量是指器件Vcc通过“R充电”给容性负载C充电，然后由容性负载C通过“R放电”释放掉的总电能量；经过整个充电和放电过程，容性负载上并无能量储存，所以所有的能量都被电阻所消耗，即，我们可认为Vcc释放出来的能量都消耗在了电阻上。

3, 所以我们得到结论：对于恒压电源充电 / 放电电路来说 ，不管串接的电阻R阻值是多少，每个充电周期消耗掉的能量是总电源能量的一半：(1/2)* CV²cc；而整个充放电周期（管脚输出一个时钟周期）消耗的能量是：C V²cc。

3. 如果器件管脚以f Hz频率循环工作，那么驱动电路的功率为：f * C* V²cc。

——举个栗子：输出10MHz时钟信号，负载电容为10pF，电压为3.3V，那么驱动功率：1010⁶Hz1010⁻¹²F3.33.3V² ≈ 1.110⁻³W = 1.1mW；这么一算单个管脚的功耗还是比较小的；但这只考虑了理想情况，后续还有跟个详细的分析。

2，叠加偏置电流的动态功耗

如上图TTL反相器的输出驱动电路在H（高电平）和L（低电平）之间较低转换，Q1和Q2交替处于导通状态，而非两者同时导通；这种电路配置有两个激励电路：一个把输出电压上拉到H，另一个将输出电压下拉到L，通常称之为推挽输出电路。TTL和CMOS都有推挽输出，如下左图为CMO推挽式输出电路。

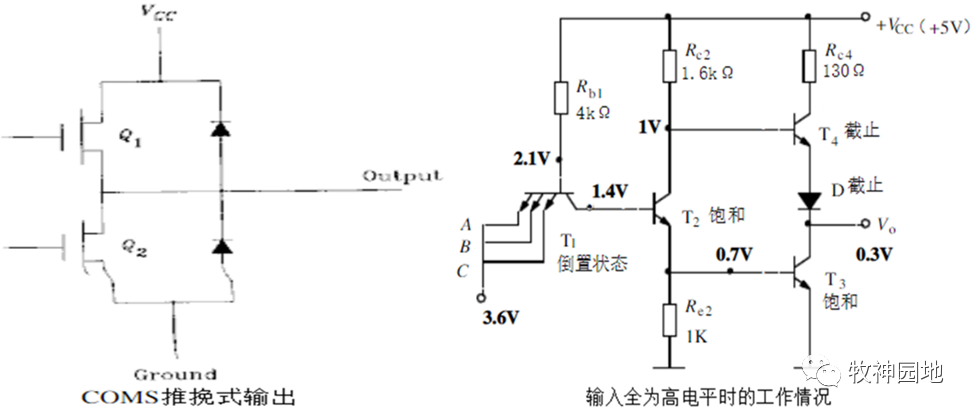
TTL推挽式输出结构工作原理如上右图所示，结构中各个器件的作用如下：

1. 二极管D保证了在T2和T3全饱和时，输出电平钳位输出是低电平，防止T3和T4同时导通产生大的交越电流；

——所有推挽式输出电路都需要有保护电路，防止高驱动和低驱动电路同时导通。

2. 如果输入电平转换很快时，每个周期都有一个交越电流并消耗一定的功耗（如下图所示），交越电流产生的额外功耗与转换速率成正比；

——对于一个快速的输入转换，重叠电流脉冲的大小和波形在每个周期都是一致的，并且每个周期消耗的能量也相同，所以这部分额外功耗与转换速率成正比，与容性负载导致的功耗不同：交越电流产生的功耗并不随电源电压的平方增加。

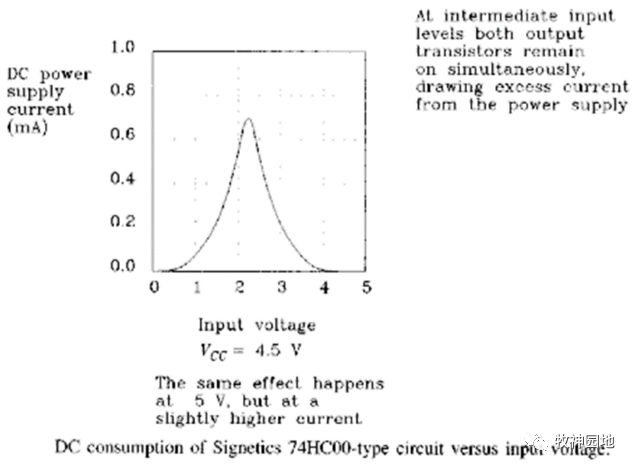
3. 减缓输入信号边沿，会导致交越时间延长；如上图为门电路典型直流电源电流与输入电压的函数关系曲线。

——减缓输入电压的转换时间往往会延长交越时间，导致T3和T4同时导通的电压附近停留的时间会更长，所以很多器件会对输入信号边沿时间有要求。

4. 对于TTL电路来说，交越效应相比CMOS更显著；如果将一个TTL反相器的输入端与其输出端相连，会产生自我偏置，从而进入交越范围内，消耗大量能量。

——因此TTL电路不适合用作线性的小信号处理器（如：振荡器），因为它们在线性工作状态是要消耗额外的能量。

3，输入功耗

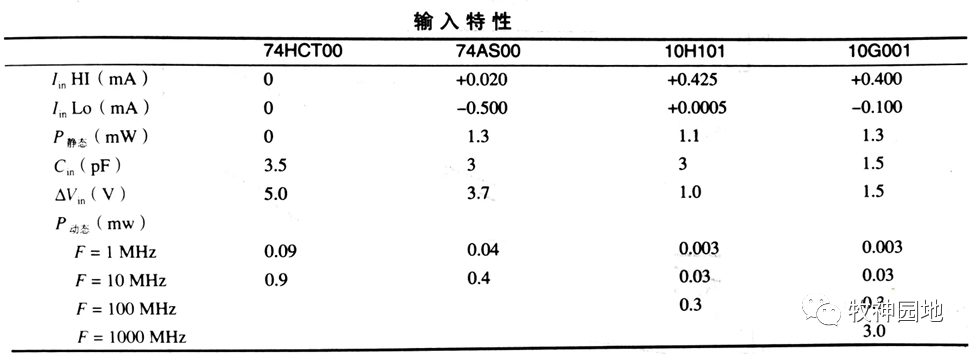
芯片的输入功耗，来自于输出器件，并由它来激活输入电路。对于输入电路的偏置和触发来说是必需的。如下表对比了4种不同逻辑器件的静态和动态输入特性：

1. 静态输入功耗：驱动电压和输入电流的乘积；它包含了接收逻辑器件内部功耗和驱动器的功耗之和。
2. 动态输入功耗：需要计算输入电容、典型供电电压和工作频率代入公式：功率 = f * C*V²cc；计算出电路驱动该输入时的总功耗。

——这些功耗相对比较小，只有较大数量扇出（Fanout）或系统要求在极低功耗运行时，才能体现其重要性。

4，内部功耗

内部功耗是指逻辑器件内部偏置电流和内部逻辑翻转的功耗，包括静态和动态功耗。

1. 静态内部功耗：是指在无负载驱动、输入端处于随机状态条件下的功耗，是所有输入状态（高/低/高阻）下的平均值；
2. 动态内部功耗：是指内部动态耗散常数“K动态”是在输出悬空，预设输入频率为时测量得到总功率P总，而后计算动态功耗常数： K动态 = (P总 – P静态)/f ；

——动态常数K动态表示周期频率每增加1Hz将额外消耗的功率。

3. 计算任意频率下的总功耗：总 = P静态 + f*K动态。

——动态频率在相对较频率（>10MHz）时才会比较明显。

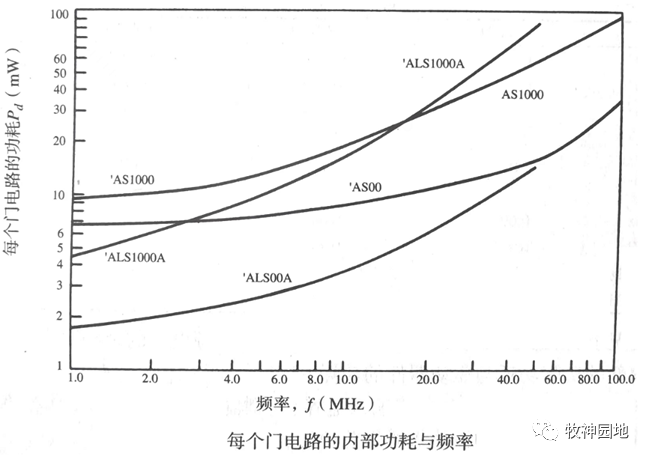
在非常宽的频率范围内，CMOS器件的内部功耗和周期频率呈明显的线性关系，这是因为CMOS电路的内部静态功耗非常低；而TTL器件由于内部静态功耗较大，所以直到工作频率接近器件的最大工作频率时才呈现出线性关系。如下图所示为不同类型TTL逻辑器件的门电路内部功耗与工作频率的关系曲线：

1. 在10MHz以上：动态功耗远大于静态功耗，总功耗曲线几乎与频率成正比；
2. 在1MHz以下：动态功耗小于静态功耗，总功耗曲线相对于频率是平坦的。

CMOS器件数据手册用等效电容Cpd来表示内部功耗，CMOS内部功耗 = Cpd * V² * f。可得到CMOS器件功耗的关联因素：

1. 与管脚工作频率和负载电容成正比；

1，器件工作频率越来越高，是整个行业的发展方向，所以不能以降低管脚工作频率为代价来减小器件功耗；

2，负载电容与器件封装技术相关，器件小型化是发展趋势，但负载电容不能无限制地减小，需要付出更多的成本代价。

2. 与I/O工作电压的平方成正比。

——减小I/O工作电压对功耗影响非常大（平方正比关系），是最明确可行的方案，举个栗子：I/O电压从5V减小至1V，那么功耗将减小至1/25；所以我们看到器件工作电压是越来越小的趋势。

5，驱动电路功耗

逻辑器件中的主要能量消耗在输出驱动电路上，而驱动电路功耗由：输出电路的结构、逻辑电平、输出负载以及运行速度决定。我们主要考虑2种输出结构：

1. 推挽电路输出；
2. 射极跟随器输出；

5.1 推挽电路输出

如下左图所示为理想TTL驱动器在H（高电平）和L（低电平）状态下的静态功耗，对于标准TTL器件来说Q2处于饱和状态（低电平）时的压降VL固定在大约0.3V；在高电平H状态下，压降由Q1的VBE和正向偏置二极管D1钳位（Vcc - VHI），约为1.4V。此时TTL驱动电流电路总静态功耗平均值近似为：P静态 = (0.3I灌+1.4I源)/2。

——此时Q1不会进入饱和状态，因为其B极电压不会上升到高于它C极电压（三极管饱和状态判断，具体参考《三极管原基础》相关章节）。

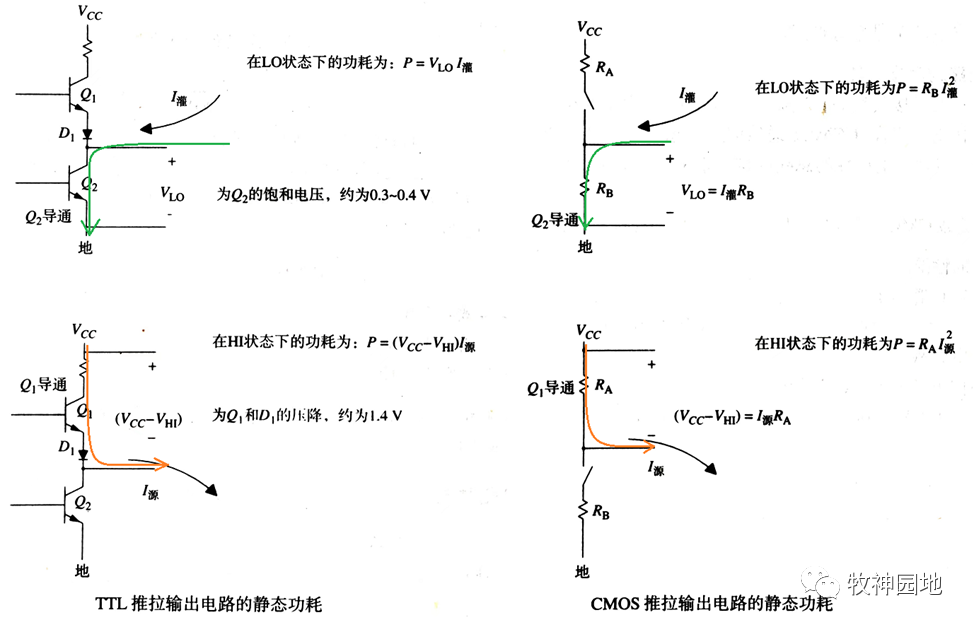
如上右图所示为CMOS驱动器电路，MOS管的导通压降很低，通常等效串联了上拉和下拉电阻；所以CMOS驱动器在高电平和低电平状态下的静态功耗：P静态 = (RbI²灌+RaI²源)/2。

——举个栗子：某器件VOL（Io = 4mA），25℃时典型值为0.15V，最大值为0.33V；某器件VOH（Io = -4mA），25℃时典型值为4.32V，最大值为3.48V；那么根据R = V/I，可计算Ra的阻抗范围是：37Ω83Ω；Rb的阻抗范围是：45Ω165Ω。在不同电源电压下，CMOS驱动器的输出电阻变化很大。

推挽电路输出负载能力，如果只按照所接负载直流输入要求进行计算，使输出负载能力达到它的直流最大扇出，特别是CMOS总线理论上的扇出能力是无限的；重负载的总线结构会带来两个问题：

1. 边沿时间会变缓；
2. 驱动器功耗增大。

输出总负载电容为：器件管脚寄生电容（10pf/pin）+PCB走线寄生电容（2pf/in）。举个栗子：我们有20个负载和10in长度的PCB走线，那么总电容 = 负载电容+走线电容 = 2010pf/pin + 10in 2pf/in = 220pF；此时信号边沿时间会变缓以及线路延迟会非常大。充电时间常数约等于驱动器输出电阻乘以输出负载电容，Trc = RC = 110Ω 220pF = 24ns（假设总线驱动器输出电阻为110Ω）。

——充电时间常数是指：电容从0充电至0.63Vcc所需的时间，升至高电平90%所需时间是Trc的两倍多：T10-90 = 2.2Trc = 53ns。

计算推挽电路动态输出功耗：f * C* V²cc；假设最差供电电压为5.5V，负载电容如上所述为220pF，信号线输出频率为10MHz，那么可得每个驱动器的功耗：1010⁶Hz22010⁻¹²F5.5V² ≈ 0.067W，如果这是一个16bit的驱动器，那么同时翻转产生的器件总功耗：P总 = 16*0.067w ≈ 1.1W。而且当上升时间缓慢时，驱动器的功耗会更高。

5.2 射极跟随器（ECL）电路输出

如下图所示为ECL射极跟随器输出电路，该电路在HI（高电平）和LO（低电平）两个状态下都有电流流过。HI（高电平）和LO（低电平）输出电压都是相近的，这些器件一般用-5.2V电源供电，高电平VHI= -0.9V，低电平VLO = -1.7V；同时射极耦合逻辑电路需要有一个上拉电阻R，用于端接至Vt = -5.2V或中间电压 -2.0V（戴维南匹配，具体参考《反射与阻抗匹配》），那么可得输出电路的静态功耗：

P静态 = (1/2) [(Vcc-Vhi) (Vhi-Vt)+(Vcc-Vlo)*(Vol-Vt)]/R

其中，Vcc =0V，VHI= -0.9V，VLO = -1.7V, Vt = -5.2V；那么计算可得：P静态 = 4.91/R。

同样，如果将R下拉至-2.0V时，可以计算得到：P静态 = 0.75/R。

那么我们可以得到：对于相同的电阻值R，使用中间电压（-2.0V）端接时表现出明显的功耗优势；这是因为当电源电压被下拉到-2.0V时，下拉电阻汲取的电流比较小（意味着低功耗）。

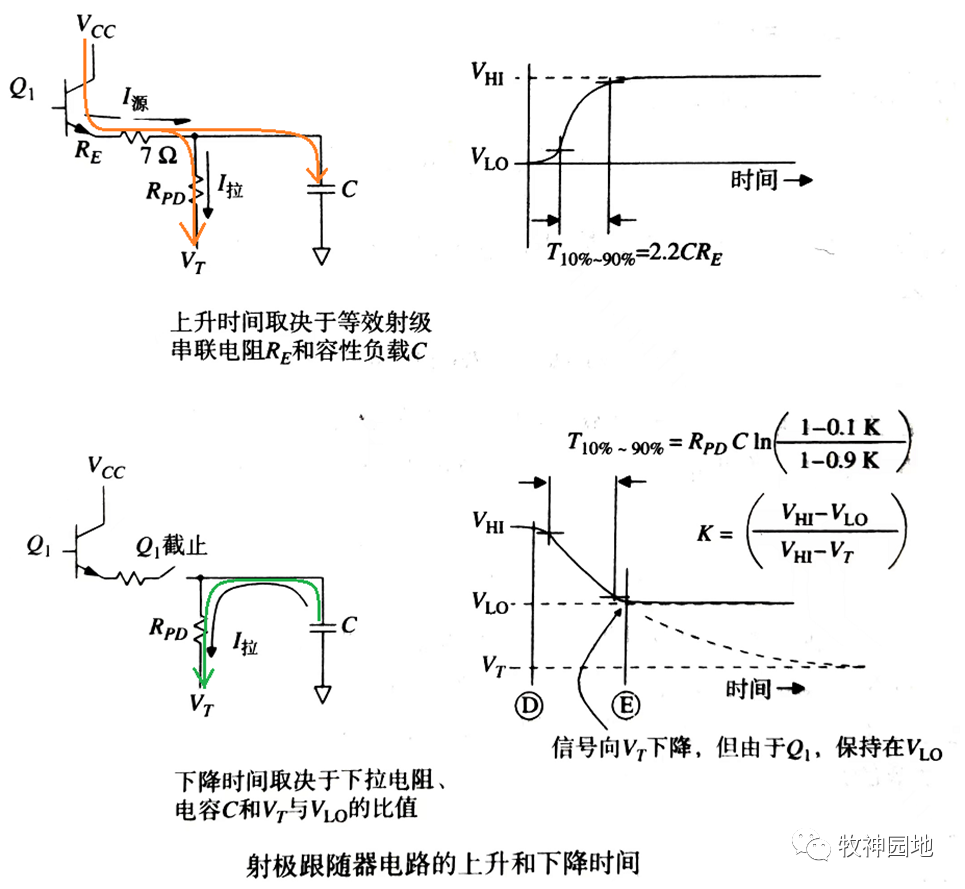
1. 如上图所示，当晶体管Q1导通（信号上升沿），电流从晶体管输出流向下拉电阻Rpd和容性负载；由于Rpd相对于Re更大，Rpd的下拉电流相对于Re输出的I源电流可以忽略不计，所以输出电压上升时间不受下拉电流的影响；

——上图中给出Re = 7Ω，当给容性负载C充电时，其充电时间常数为：Trc = Re* C；而充电至90%所需的时间为T10-90 = 2.2*Trc。

2. 当晶体管Q1截止（信号下降沿），从而不再有电流流过发射极；只有容性负载C通过下拉电阻Rpd放电：下降时间与电容C放电的速度成正比，功耗与静态下拉电流成正比；此时需要有一个大电流迅速地将电容C放电；

——如果Q1完全截止（忽略其漏电流），从90%-10%的下降时间为：T90-10 = RpdCln[(1-0.1K)/(1-0.9K)]；其中常数K = (Vhi-Vlo)/(Vhi-Vi)；如上面栗子参数（Vt = -5.2V），可计算K = 0.186， T90-10 = 0.164RpdC。若Vt = -2.0V，那么计算K = 0.727，T90-10 = 0.987RpdC。

3. 当Vt = -2.0V时虽然功耗相对较小，但是边沿时间会更长，为了达到相同的相同时间，必须要求所采用的下拉电阻相比于Vt = -5.2V电阻的阻值更小，而一旦选择了较小的电阻，其两种匹配方式的功耗数也大致相等。

——同时考虑其它方面：1，采用Vt = -5.2V不需要引入单独的新电源；2，采用Vt = -2.0V时下拉电阻范围在50100Ω，正好可以作为线路的终端匹配（阻抗匹配），而Vt = -5.2V时端接电阻在330680Ω，不适合做终端匹配（关于终端匹配相关知识参考：《反射与阻抗匹配》章节内容）。

4. ECL输出电路相对于推挽输出电路的好处是：

1, 由于电压摆幅小，所以电路动态功耗非常小（下拉电阻产生的损耗）；

2, 没有推挽输出电路的高低电平切换“死区时间”，切换的速率更快，且无额外损耗。