电源变换器基础（2）-开关电源中的电感

二，开关电源中的电感器

开关电源主要由：开关管（BJT/MOS管），续流二极管（肖特基二极管/快恢复二极管），电感器以及电容器组成；关于这些元件的基本特性，我们在之前的各个专题中已经学习了，当然各位胖友们可能已经忘了个精光，不过没关系，多复习才能更好的掌握嘛；接下来会粗略回顾一下这些器件的某些特性，至于具体原理，我会具体备注要去回顾那个专题的内容。

1，电感器和电容器

我们再来回顾一遍电容的定义：两个导体在一定电压下存储电荷能力的度量。根据电容的定义可得C = dQ/dV，它与电压有直接的关系；而电感L=dφ/dI，与电流有直接的关系，其特性类似于电流源。电容器储存的是静电场能，而电感器储存的是磁场能量，所以从直观上我们对电容器会更加容易理解一些（能够通过示波器直观“感受”到电压而理解电场能量），而对电感器的理解则困难的多，如果对电感器原理已经忘记了，建议再快速回顾一遍（《电感特性原理》和《电感器原理》专题）。

电感和电容特性是对偶的（具体参考《电感器原理》的“理想电感器与电容器”章节），即将电感看成电容的镜像（在电感和电容元件的电压-电流方程中，电压项与电流项互换，可以使方程相互转化），所以从本质来说电容与电感类似，电压与电流类似。如下图所示，为电感和电容的充电电路，电容充电时间常数τ=RC，电感充电时间常数τ=L/R。

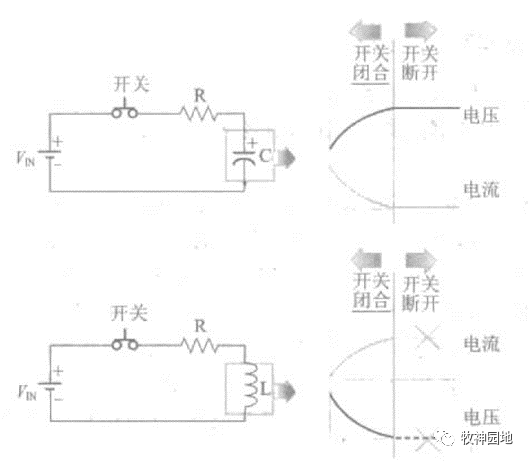
但是如上图所示，其并非是真正的对偶关系，因为在开关打开后的部分，电容器电压/电流保持不变；而电感器的电压/电流则是一个未知状态：开关打开后，通过L的电流大小保持不变，此时电流（自由电子）由开关至电感之间的元件和走线提供，所以电感上方会出现一个高负压，电感器外部形成从下而上的电场，最后导致电感器高压电弧放电。

我们在开关电源的实际工作中，电感器并不会串联一个电阻器来进行限流，如上图所示，电感器串联电阻R = 0时，会发生什么现象？

1. 在开关闭合的瞬间，由于电阻器R两端没有压降，根据基尔霍夫第二定律（电压定律），电感器两端电压就是Vin（外部输入电源电压）；
2. 随着时间的变化，电感器两端的电压一直保持不变：Vin；

——电感器两端外加电压为Vin，那么电感器必然会产生大小相同、反向相反的感应电压（-Vin），所以就算绕组导线的电阻值非常小，也不会过流烧毁电感器（具体参考《电感器原理》中“电感器的基本原理”章节）。

3. 此时通过电感器的电流以恒定斜率持续增加，理论上将达到无穷大：dI(t)/dt = Vin/L。

——因为只要电感器两端存在电压，电感器电流就必须有变化（变化率是常数，其值为Vin/L），直到磁饱和，最终过流并烧毁电感器；如果流过电感器的电流不变，那么电感器的阻抗为0（相当于一条导线），根据I = V/R可得：电流就会急剧增大。

2，电感器放电

我们在上一节分析了电感器在电压源下开关关断瞬间的状态，如下图所示，电感器两端出现极高的电压（负压），同时电流以陡峭的斜率迅速下降为0。但是在开关关断瞬间，电感器两端的电压尖峰值是多少呢？

我们先来做定性分析：在开关关断阶段，根据电感器的特性，电流始终要保持连续，而电感器两端触点的电压会急剧增加直至形成一个短电弧。如果触点间距增加，那么电压会自动增加以触发电弧，此时电流将以陡峭的斜率直线下降，而且只要电感器有储能，那么电弧就会一直持续，直到电流完全为0（电流下降斜率为V/L），因此最终要将全部电感储能化作电弧，以光和热的形式泄放掉。

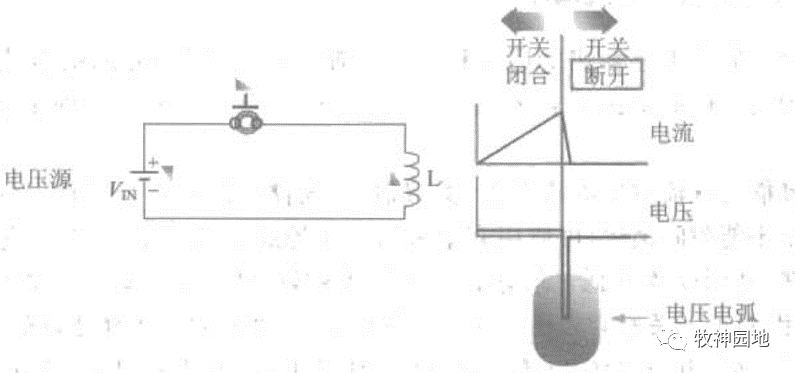
在开关关断时，电感器中必须泄放的能量称为反激能量，强迫连续导通的电流称为续流电流。电感器的储存能量的大小与流过电流大小有关：P =1/2 * L* I²，如果流过电感器的电流不连续，那么意味着能量也不连续，这是不允许发生的事情。但是电流的变化率：dI/dt是可以瞬间改变的，如下图所示：

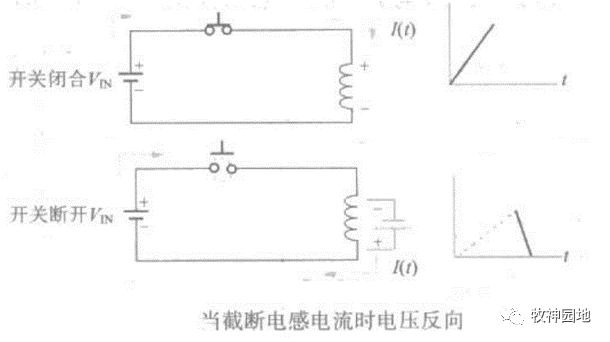
1. 开关闭合时电流从直流电压源正端流出，所以电感器上端电压高于下端电压；
2. 此后断开开关，电流要保持连续，且与原电流方向相同，因此此时电感看成一个电压源（电压源从正极流出，流入负极），维持电流连续，使得电感器下端电压高于上端电压；
3. 从这个角度来看，为维持电流连续，电感器电压需要发生反向；流过电感器的电流从一条具有上升斜率（储能）的曲线跳变成下降斜率（释放能量）的曲线。

——用电感器本身特性来分析其电磁感应电压的方向：电感器要阻止其内部电流的变化；所以当开关闭合时电感器电流增加，感应电压与电流方向相反（上低下高）；当开关断开时电感器电流减小，感应电压与电流方向相同（上高下低）；所以我们看到在开关闭合和断开时，电感器的感应电压方向是不同的。

3，开关电源变换器中的电感器

如下图所示，电感器电流在开关闭合时经正向电压（VON= VIN-VO）作用上升，在开关断开后必然受到反向电压（VOFF= 0-VO）作用下降。通过电感方程V = LΔI/Δt可得，VON = LΔIon/ton；VOFF = L*ΔIoff/toff。如果开关导通阶段的电流增量（ΔIon）恰好等于开关关断阶段的电流减量（ΔIoff），那么我们可以认为电源电路达到了稳态，即：每一个开关周期都准确复制了上一个开关周期，为输出电容器和负载持续不断的传输稳定（完全相同）的能量包。

——在开关电源实际工作中，稳态只是暂时的状态，一般情况下在后续各开关周期内，电流的净增量或净减量会逐步积累，电路状态是持续变化的。

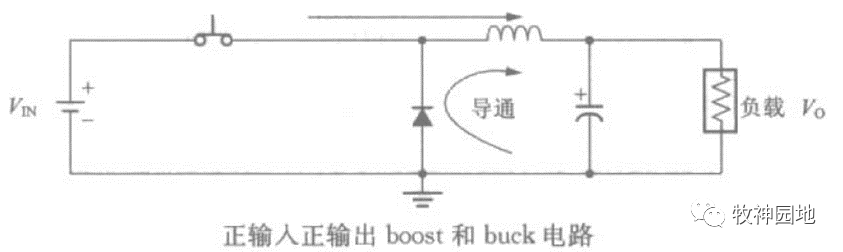
当然要让电路达到稳态也并非是很困难的事情，只要输入电压和输出负载稳定，再通过电源环路稳定性设计，电源会自发地达到稳态工作，并一直保持下去。所以任何开关电源拓扑必须要能达到ΔIon = ΔIoff所描述的状态，若达不到则不是一个有效拓扑；然而电感方程和稳态定义仅涉及电流的增减量（ΔI），并不涉及开关周期内的电感器电流绝对值。根据在开关周期内电感器电流的状态不同，分为多种模式：

1. 连续导通模式（CCM）：电流在每个开关周期内都会回复到0（如下图阴影部分：VONton = VOFFtoff）；在所有情况下电感器电压在开、关状态下总是反向的，而且电流上升斜率为VON /L，电流下降斜率为VOFF /L；

——根据伏秒定律，图中两块阴影区域的面积必然相等（VONton = VOFFtoff），所有达到稳态的工作模式都满足该条件。

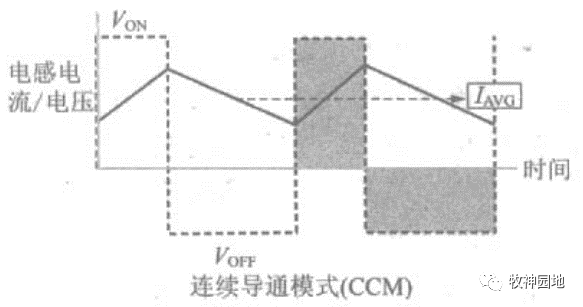
2. 临界导通模式（BCM）：降低电感器电流最小值至0，正好介于连续导通和断续导通模式之间，我们可以将它看作是连续导通模式的一种；

——当然也可以看成断续模式的一种，但是连续导通模式相对更加简单。

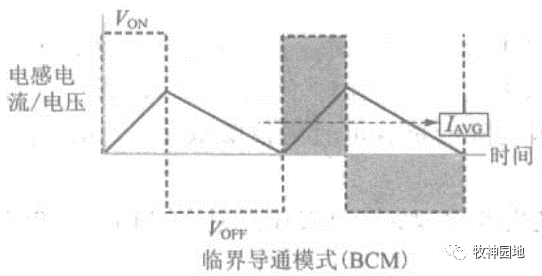
3. 断续导通模式（DCM）：电流无论如何变化，其值始终大于0；

——该模式在非同步开关电源拓扑中，续流二极管的反向截止阻断了反偏电流，并防止电感电流变负，此时电感电流保持为0，所以其储能为0，电感电压也为0；断续导通模式下，有一段时间电感器中并无电流流过，因此平均电感器电流计算比较复杂，导致断续导通模式下的方程看起来非常复杂。

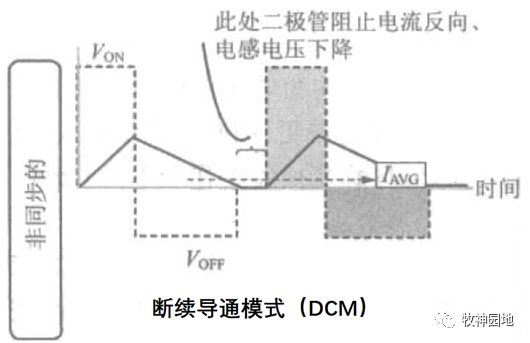
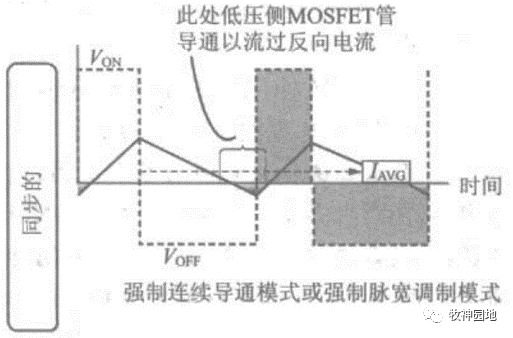
4. 强迫连续导通模式（FCCM）：采用MOS管替代续流二极管（同步开关电源），允许续流电流反向流过，从而允许电感器电流变为负值（反向流动）；此时电感器电压保持不变，因为电流变化的趋势不变，电感器继续储能。

——虽然电感器中会出现负电流（反向电流），但是其平均电流为正，因为能量传输的方向整体是从电源流向负载端的（可用坡印亭矢量分析）。

——同步拓扑中的MOS管的导通压降远低于二极管，使得续流器件的导通损耗显著降低，而且允许电感器反向流过电流，此时变换器就不会转换到断续导通模式。

有一个问题是：平均电感电流（IL）与负载电流（IO）有什么关系呢？

这取决于不同的拓扑，在降压拓扑中：

1. 平均电感电流就是负载电流（IL=IO），因为电感器串接在输出端，所有输出电流必然经过电感器；
2. 在升压拓扑和升降压拓扑中：平均电感电流（IL）与负载电流（IO）成正比。
3. 所以我们得到一个结论：任何拓扑，只要降低负载电流（IO）就可以降低平均电感电流（IL）。

4，伏秒定律

上面我们已经提到了一下伏秒定律，那什么是伏秒定律呢？

还是先从电感方程开始：V = L* ΔI/Δt，当电源处于稳态时：ΔIon = ΔIoff = ΔI；所以VONton = LΔIon = LΔIoff = VOFFtoff；就可以得到了结论，在电源电路稳态时：VONton = VOFFtoff；好，那我们知道V是电压（单位：伏），t是时间（单位：秒），电感器电压与作用时间的乘积就称为：伏秒积。

——电源稳态时要求：开关导通阶段（电感器电流上升）伏秒积的幅值必然等于关断阶段（电感器电流下降）伏秒积的幅值，但符号相反。

如果用图来表示，如下图所示，开关导通和关断阶段的电压和时间的乘积为阴影部分，两者面积必然相等。即稳态工作时，任何开关周期内，电感器电压曲线的净面积必然为0。现在开关电源的工作频率都很高（几百KHZ以上），所以伏秒积是一个很小的值，为了便于处理使用Et（伏微秒积）来表示，而开关电源变换器中的电感器感值一般也是以uH计算，所以可以将公式变为：ΔI = Et/L；其中L单位为uH。

那如果电路并非处于稳态，即电感器电流没有回复到初始状态，会发生什么事情呢？

开关电源中电感器电流满足ΔIon = ΔIoff的条件，表示电感器复位成功（电感器能量储存增加的量 = 能量消耗减少的量）；如果没有复位成功，那么电感器电流就会持续增加（或减小），直至超过电感器的额定电流，从而导致电感器磁芯饱和或烧毁，这样的开关拓扑是不稳定的；即：任何电感器无法复位的电路结构都不可能称为有效的开关拓扑。

我们从伏秒定律公式：VONton = VOFFtoff可得：ton/toff = Voff/Von = Vo/(Vin-Vo)；定义电源变换器占空比D为开关的导通时间与开关周期之比，D = ton/T = ton/(ton+toff) = Vo/Vin；其中toff = T – ton仅在连续导通模式下成立。我们可以看到通过伏秒定律得到了降压拓扑下，占空比与输入/输出电压的关系。

——同样根据能量守恒原理，假设在理想情况下电源转换效率为100%（Pin = Po），Pin = VinIinton（一个周期内只有ton时间内输出功率），Po= VoIoT（在整个周期连续输出功率）；由于在稳态时Iin平均电流与整个周期内电流相等Iin = Io = I，所以Pin = VinIton = Po = VoIT，可得Vinton = VoT，占空比：D = ton/T = Vo/Vin。