

机器学习笔记之高斯过程(下)
电子说
描述
我们可以将输出绘制成输入的函数图像。下面的线只是一个常规的非随机函数,即weight=g(height)或y=g(x)。
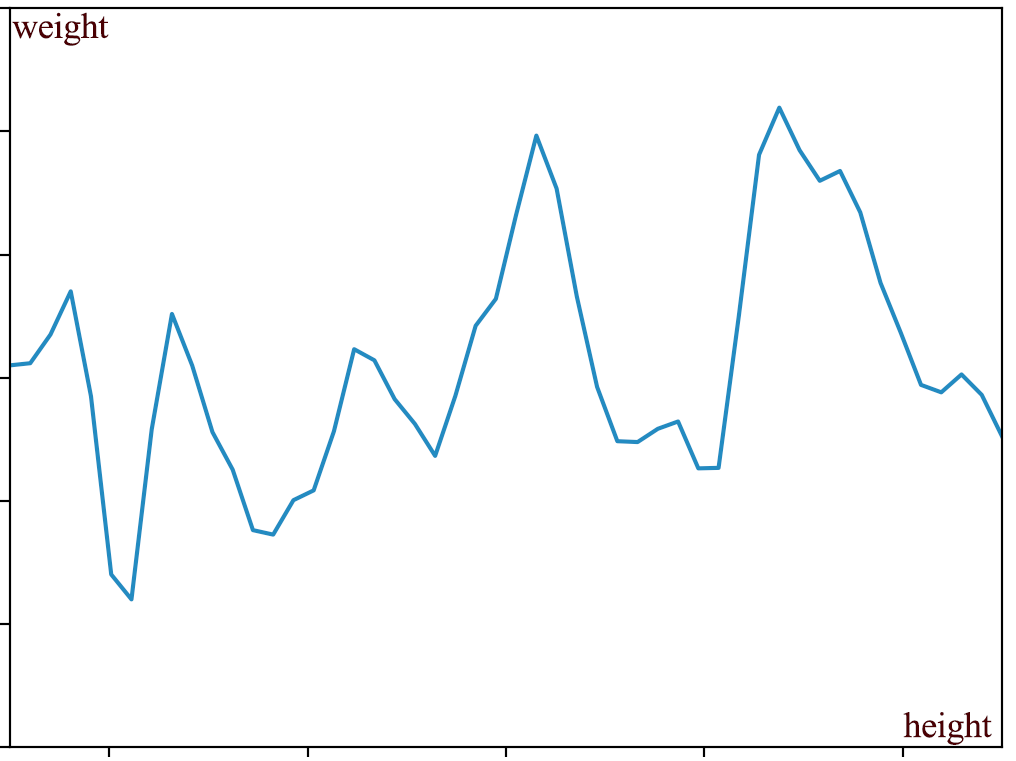
在本节中,我们使用符号g(x)表示一个非随机函数,而使用f(x)表示一个随机函数。
为了更轻松地生成训练数据,我们将切换到一个新模型y=sin(x)。我们使用这个方程生成2个训练数据点(下面的2个蓝点)来构建一个高斯模型。然后从 中采样三次,如下面的三条实线所示。
中采样三次,如下面的三条实线所示。

我们看到,这2个训练数据点强制 在蓝点相交。如果我们持续采样,我们将开始直观地识别每个
在蓝点相交。如果我们持续采样,我们将开始直观地识别每个 的
的 的平均值和范围。例如,下面的红点和蓝线估计了
的平均值和范围。例如,下面的红点和蓝线估计了 =−3.8时
=−3.8时 的均值和方差。由于
的均值和方差。由于 介于2个训练点之间,因此估计具有相对较高的不确定性(由σ表示)。
介于2个训练点之间,因此估计具有相对较高的不确定性(由σ表示)。

在下面的图中,我们有5个训练数据,并从 中采样30条线。红色虚线表示
中采样30条线。红色虚线表示 的均值输出值
的均值输出值 ,灰色区域是离
,灰色区域是离 不超过2
不超过2 的范围。
的范围。
如前所述,每条线都像一个函数,将输入映射到输出:y=g(x)。我们从许多可能的函数g开始,但是训练数据集会降低或增加某些函数的可能性。从技术上讲, 模拟了给定训练数据集的函数g的可能性分布(上述绘制的线的概率分布)。
模拟了给定训练数据集的函数g的可能性分布(上述绘制的线的概率分布)。
高斯过程(GP)的特点是构建高斯模型来描述函数的分布。
我们不会通过采样来解决这个问题,而是通过分析方法来解决。
回到:

我们可以将表达式推广为以下形式,其中f是训练集的标签(体重), 是我们要预测
是我们要预测 的体重。现在我们需要使用高斯模型来解决p(
的体重。现在我们需要使用高斯模型来解决p( |f)的问题。
|f)的问题。

回想一下之前关于多元高斯定理的部分,如果我们有一个模型:

我们可以通过以下方式求 :
:

现在,我们应用这些公式来解决p( |f)的问题:
|f)的问题:

对于训练数据集,假设输出标签f服从高斯分布:

并且假设 的高斯分布为:
的高斯分布为:

其中,L定义为:

然后根据多元高斯定理,我们有:

我们将应用这些公式来模拟采样自y=sin(x)的训练数据。在这个例子中,由于sin函数的均值为0,所以μ= =0。因此,我们的方程将简化为:
=0。因此,我们的方程将简化为:

请注意,矩阵K可能难以求逆。因此,我们首先应用Cholesky分解对K进行分解,然后应用线性代数来解决 。
。

表示使用线性代数方法来求Ax=b方程的解x。
在求 之前,我们需要预先计算一些项:
之前,我们需要预先计算一些项:

应用 和上面的方程:
和上面的方程:

现在我们有计算 和
和 的方程:
的方程:
代码
首先,准备训练数据,并通过sin函数打标签。训练数据包含5个数据点( =−4,−3,−2,−1和1)。
=−4,−3,−2,−1和1)。
Xtrain = np.array([-4, -3, -2, -1, 1]).reshape(5,1)
ytrain = np.sin(Xtrain) # Our output labels.
测试数据:我们创建50个新数据点,在-5和5之间线性分布,由高斯过程进行预测。
# 50 Test data
n = 50
Xtest = np.linspace(-5, 5, n).reshape(-1,1)
在这里,我们定义一个核函数,使用指数平方核度量两个数据点之间的相似性。
# A kernel function (aka Gaussian) measuring the similarity between a and b. 1 means the same.
def kernel(a, b, param):
sqdist = np.sum(a**2,1).reshape(-1,1) + np.sum(b**2,1) - 2*np.dot(a, b.T)
return np.exp(-.5 * (1/param) * sqdist)
计算核(K, ,
, ):
):
K = kernel(Xtrain, Xtrain, param) # Shape (5, 5)
K_s = kernel(Xtrain, Xtest, param) # Shape (5, 50)
K_ss = kernel(Xtest, Xtest, param) # Kss Shape (50, 50)
我们将使用Cholesky分解对K进行分解,即 。
。
L = np.linalg.cholesky(K + 0.00005*np.eye(len(Xtrain))) # Shape (5, 5)
计算我们的预测的输出均值 。由于我们假设μ∗=μ=0,因此该方程变为:
。由于我们假设μ∗=μ=0,因此该方程变为:

L = np.linalg.cholesky(K + 0.00005*np.eye(len(Xtrain))) # Add some nose to make the solution stable
# Shape (5, 5)
# Compute the mean at our test points.
Lk = np.linalg.solve(L, K_s) # Shape (5, 50)
mu = np.dot(Lk.T, np.linalg.solve(L, ytrain)).reshape((n,)) # Shape (50, )
计算 σ
# Compute the standard deviation.
s2 = np.diag(K_ss) - np.sum(Lk**2, axis=0) # Shape (50, )
stdv = np.sqrt(s2) # Shape (50, )
采样 以便我们可以绘制它的图像。
以便我们可以绘制它的图像。

使用μ和L作为方差来对其进行采样:

L = np.linalg.cholesky(K_ss + 1e-6*np.eye(n) - np.dot(Lk.T, Lk)) # Shape (50, 50)
f_post = mu.reshape(-1,1) + np.dot(L, np.random.normal(size=(n,5))) # Shape (50, 3)
我们采样了3个可能的输出,分别用橙色、蓝色和绿色线表示。灰色区域是离μ不超过2σ的范围。蓝点是我们的训练数据集。在蓝点处,σ更接近于0。对于训练数据点之间的点,σ增加反映了它的不确定性,因为它不接近训练数据点。当我们移动到x=1之外时,就没有更多的训练数据了,并且导致σ变大。

这是另一个在观察5个数据点后的后验概率图。蓝点是我们的训练数据点,灰色区域展示了预测的不确定性(方差)。

高斯混合模型
高斯混合模型是一种概率模型,它假设所有数据点都来自于高斯分布的混合物。
对于K=2,我们将有两个高斯分布G1=(μ1,σ21)和G2=(μ2,σ22)。我们从随机初始化参数μ和σ开始。高斯混合模型尝试将训练数据点适合到G1和G2中,然后重新计算它们的参数。数据点被重新拟合并且参数再次计算。迭代将继续直到解决方案收敛。


EM算法
使用随机值初始化G1和G2的参数(μ1,σ21)和(μ2,σ22),并将P(a)=P(b)=0.5。
对于所有的训练数据点x1,x2,⋯,计算它属于a(G1)或b(G2)的概率。

现在,我们重新计算G1和G2的参数:

重新计算先验概率:

对于多元高斯分布,其概率分布函数为:

-
PyTorch教程18.1之高斯过程简介2023-06-05 649
-
机器学习笔记之高斯过程(上)2023-05-30 2355
-
什么是高斯过程 神经网络高斯过程解析2022-08-10 5111
-
高斯过程回归GPR和多任务高斯过程MTGP2021-06-30 1674
-
机器学习的个人学习笔记2021-03-01 1135
-
机器学习笔记之BP推导2020-06-15 1539
-
吴恩达机器学习笔记分享2020-06-05 1535
-
机器学习基石笔记2020-05-26 1026
-
基于高斯过程回归学习的频谱分配算法2017-11-30 1029
全部0条评论

快来发表一下你的评论吧 !

