基于波前编码的扩展景深短波红外成像系统

短波红外波段具备全天时、全天候成像的优良潜力，借助焦平面探测阵列在现代社会发挥着日益重要的作用。为了解决短波红外成像系统的离焦问题以提升平台适用性，可将波前编码技术引入短波红外波段。

据麦姆斯咨询报道，近期，中电科五十四所和桂林电子科技大学的联合科研团队在《激光与光电子学进展》期刊上发表了以“基于波前编码的扩展景深短波红外成像系统”为主题的文章。该文章第一作者和通讯作者为中电科五十四所王伟。

本文将波前编码引入短波红外波段，相比常规的单一性评价标准，采用综合离焦一致性和图像可恢复性的复合标准，解决离焦对成像质量的影响，对提升载荷的平台适应性和环境适应性具有一定的参考价值。

基于波前编码技术的景深延拓原理

波前编码的基本原理如图1所示。与常规成像系统相比，波前编码在光瞳位置放置特殊设计的相位板，利用波前光程差的变化改变相位，依据一定的评价函数得到对离焦去敏的、具备一定相似性的中间模糊图像，最后利用计算机图像处理算法复原图像。

点扩散函数描述光学系统对点光源的输出响应，理想的点扩散函数近似能量集中的小支持域脉冲函数。在经典光学理论中，光学成像过程是物空间目标和点扩散函数的卷积。波前编码系统牺牲能量集中度以扩大点扩散函数支持域，从而降低系统对离焦的敏感度。

光学传递函数取模运算即为调制传递函数，调制传递函数取平方即为点扩散函数，这两个函数均与离焦参数Ψ无关，仅与相位板参数α有关，即波前编码系统表现出良好的调制传递函数一致性或点扩散函数一致性。这是波前编码的理论基础，据此可以用同一图像处理算法复原图像，波前编码系统的设计可简化为对相位板参数的优化。

短波红外波前编码系统设计与仿真

短波红外光学系统优化

为验证波前编码的有效性，对一台轻小型大视场短波红外相机进行优化，采用25 μm像元尺寸InGaAs焦平面探测器，以空间频率表示的极限分辨率（即单位长度能够分辨的黑白线对数）约为20 lp/mm。光学系统指标参数如表1所示。

表1 光学系统指标参数

波前编码相位板通常放置在系统光瞳位置，光学系统初始结构采用如图2（a）所示的准对称平场双高斯物镜，可以消除轴向像差。依据设计指标对初始结构进行调整，按照0.6的比例因子将初始结构缩放到指定焦距，更改初始系统的工作波长、通光孔径、视场角。在保证像质的前提下，综合考虑玻璃材料的光学、热力学等理化性质，选择透过率高和热膨胀系数低的ZnSe和BaF₂材料。

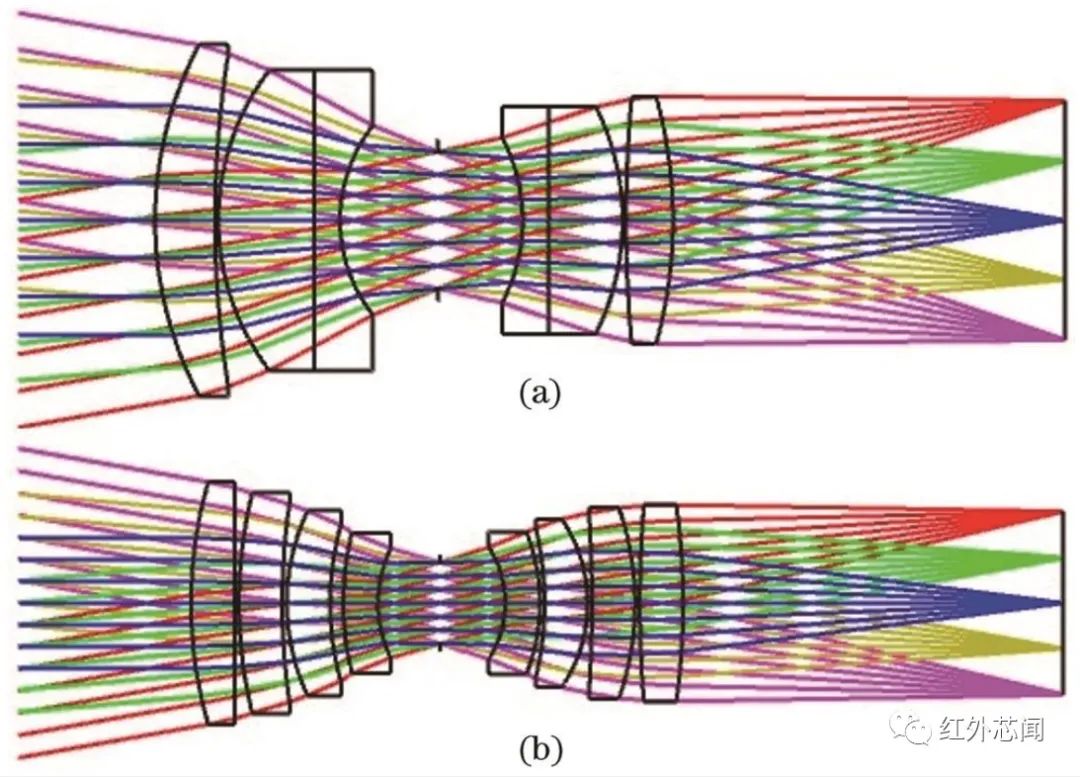
图2 光学系统结构示意图：（a）初始结构；（b）优化后的结构

利用几何光线追迹理论和阻尼最小二乘法对初始结构进行迭代优化，优化后的光学系统如图2（b）所示，最佳焦面后截距为44.003 mm，光阑前后预留7.193 mm和7.523 mm用于安置相位板。分离胶合透镜以增加光学设计自由度，提高对像差的控制能力，相较于双胶合透镜无需严格地匹配光焦度，适度增大空气间隔以减小欠校正像差。适度增加前组中高折射率ZnSe透镜光焦度，减轻低折射率BaF₂透镜光焦度负担，避免曲率半径过小。将前后组中的BaF₂透镜分裂为两个透镜以避免透镜中心厚度过大。离轴视场光线沿径向位置的焦点偏离焦平面产生场曲和像散，在焦面一侧添加场镜校正场曲和像散。

图3为0°中心视场下光学系统在不同离焦参量下的调制传递函数曲线。其中，子午面和弧矢面函数值取平均。可以看出，在理想焦平面位置，在截止频率范围内像质良好，调制传递函数曲线接近衍射极限。随着像面偏离理想焦平面，调制传递函数曲线迅速衰落，相同倍率下正向和负向离焦变化趋势相同。在±5倍景深（±0.208 mm）离焦下，调制传递函数曲线迅速降低；在±10倍景深（±0.416 mm）离焦下，调制传递函数曲线出现零点，导致信息丢失和对比度反转；在±15倍景深（±0.624 mm）和±20倍景深（±0.832 mm）离焦下，调制传递函数曲线零点依次增多。

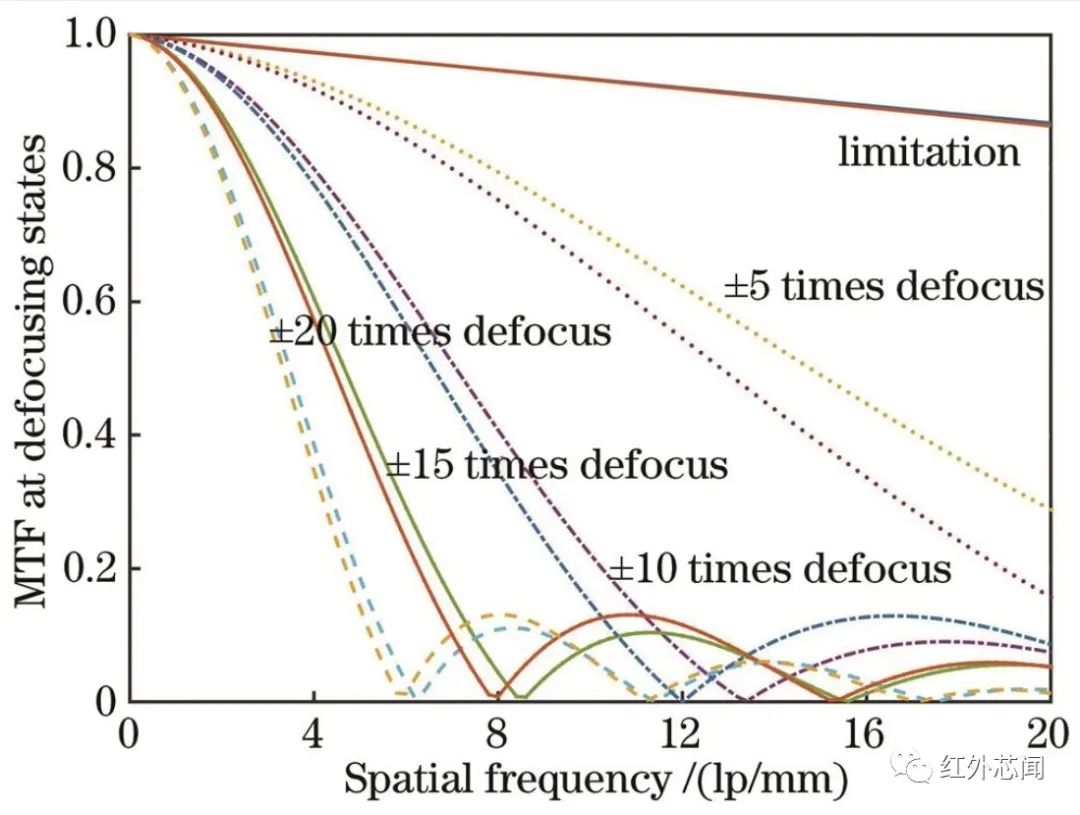
图3 不同离焦状态下的光学系统调制传递函数曲线

波前编码系统优化设计

在保持短波红外光学系统不变的基础上，在光阑位置插入特殊设计的三次方型相位板降低系统离焦敏感性。三次方型相位板采用2 mm厚度硅基玻璃材料制作，中心波长1.3 μm处折射率为1.598。采用扩展多项式面型模拟相位板前表面，相位板后表面采用标准平面，孔径光阑置于后表面。

常规相位板参数优化通常采用单一评价标准，缺乏对模糊图像可恢复性的讨论。依据前述卷积成像理论，成像过程是物空间目标与点扩散函数的卷积，图像复原过程是低通滤波过程，点扩散函数的中心点能量决定了系统的信噪比，近似等于调制传递函数曲线与坐标轴包围的面积。为了获得足够高的信噪比，需要对波前编码系统点扩散函数的幅值加以约束。综合考虑离焦一致性和图像可恢复性，结合调制传递函数和点扩散函数关系，所采用的相位板参数优化策略遵守以下两条原则：1）截止频率内调制传递函数具备离焦一致性；2）全频率内点扩散函数幅值的能量相对集中。

光学设计软件可以获取不同离焦参量下离散空间频率对应的调制传递函数值，图4为不同径向坐标系数下的波前编码系统调制传递函数曲线变化趋势图，用以说明调制传递函数的离焦一致性，采用0°中心视场成像，依次对应±5、±10、±15、±20倍景深离焦。

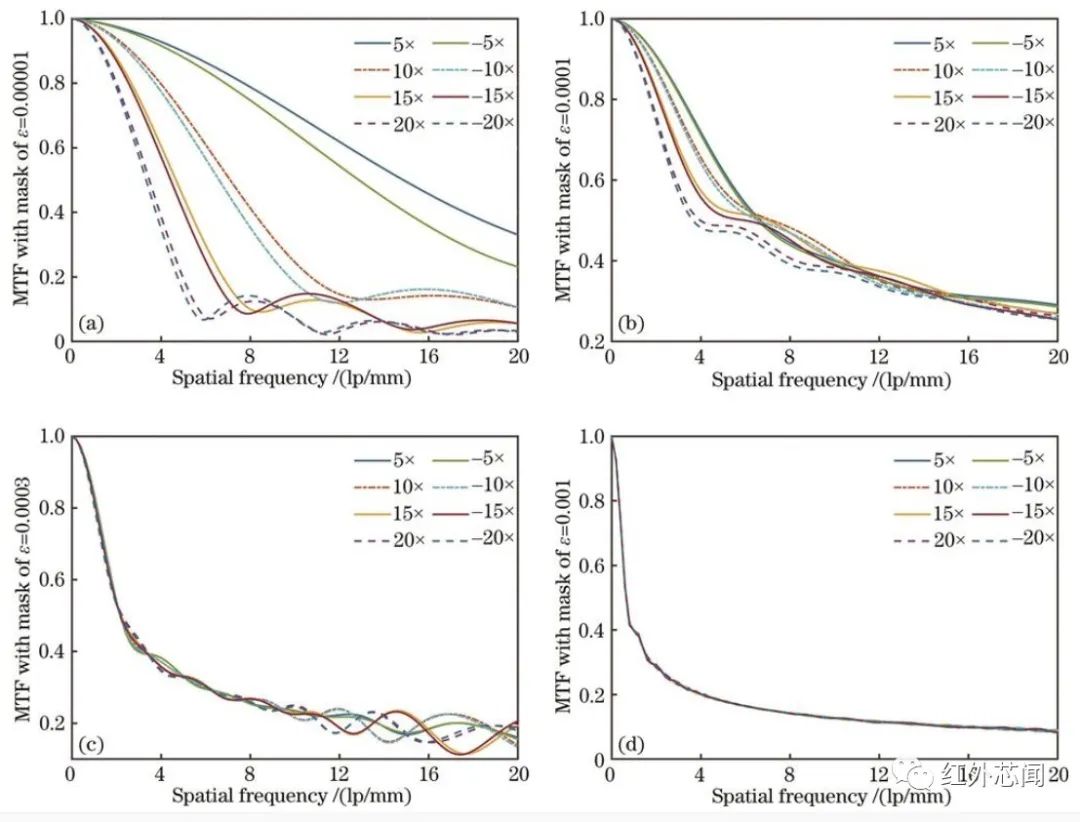
图4 不同相位参数下波前编码系统调制传递函数曲线

随着径向坐标系数的增加，调制传递函数的离焦一致性得到改善。在径向坐标系数取极小值1×10⁻⁵时，调制传递函数曲线出现不同程度的提升，函数零点导致的信息丢失和对比度反转现象消失；在径向坐标系数取1×10⁻⁴时，调制传递函数曲线在0~10 lp/mm频率范围内差异性显著；这种差异性随着径向坐标系数的进一步增大向高频方向转移，径向坐标系数取3×10⁻⁴时，差异性主要集中在10~20 lp/mm频率范围内；当径向坐标系数高于1×10⁻³时，调制传递函数曲线趋向于一致，呈现出良好的离焦一致性。

为定量评价相位板参数，引入离散积分、欧氏距离、余弦相似性，分别用于表征调制传递函数的差异性和相似性。调制传递函数均为离散采样点，利用矩形近似和极限原理计算定积分。离散积分准确性与采样率相关，采样间隔Δu取0.2 lp/mm。

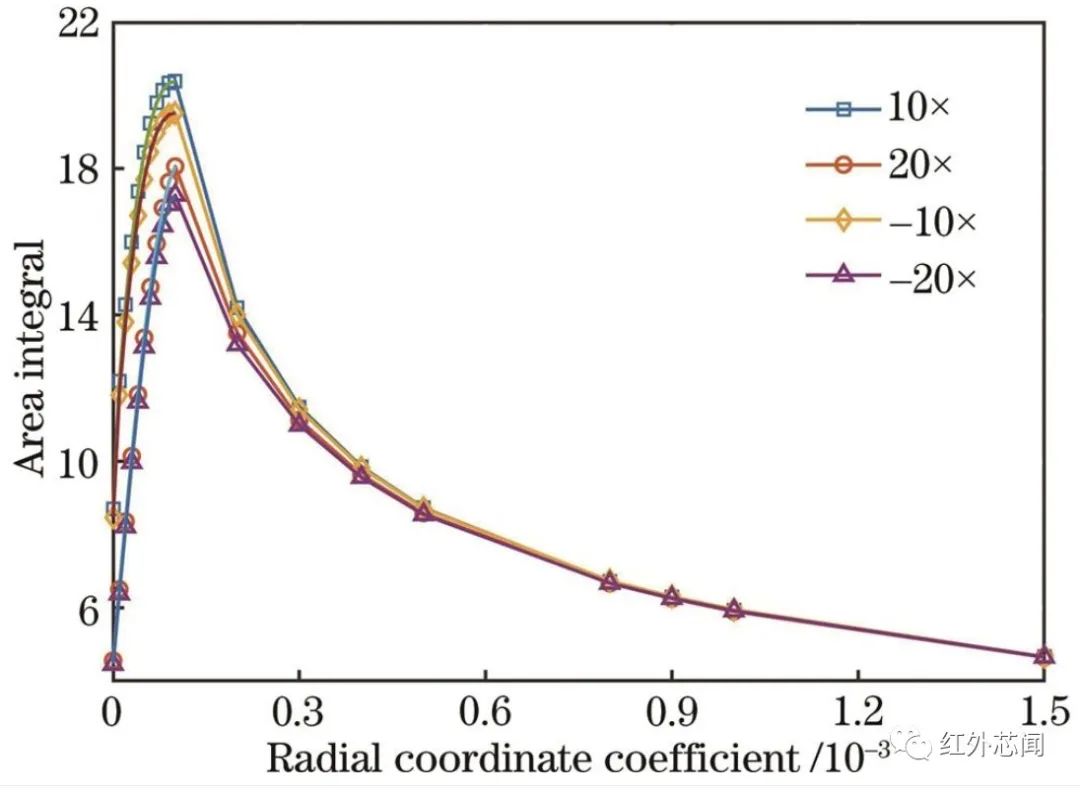
图5 不同离焦状态下的调制传递函数积分曲线

欧氏距离即欧几里得度量，在一维空间中可以表征两点之间的差异，与均方根误差具有相似性和关联性。

不同径向坐标系数下，±10倍和±20倍景深离焦欧氏距离曲线如图6所示，纵坐标取对数以直观展示数据。理论上，差异显著性与欧氏距离成反比，离焦一致性良好的调制传递函数具有相似的欧氏距离数值。随着径向坐标系数的增大，欧氏距离数值接近0，表明不同离焦参量下的调制传递具有良好的一致性。

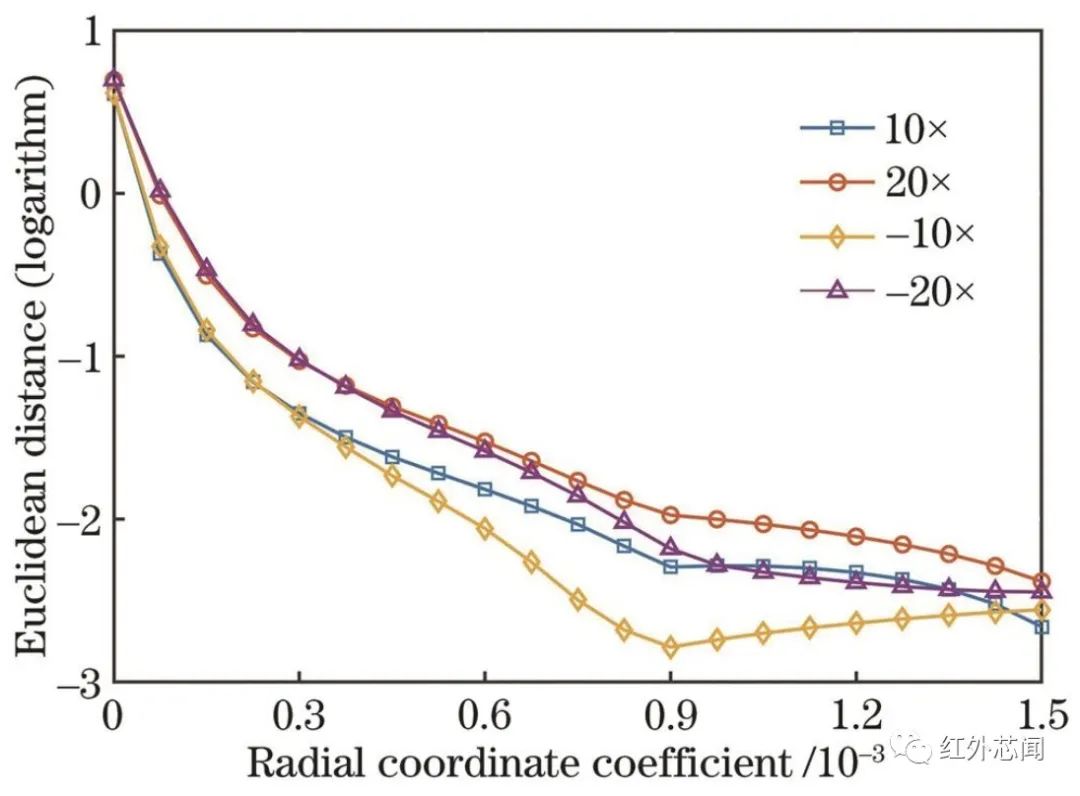
图6 不同离焦状态下的欧式距离曲线

余弦相似性通常用来表征二维空间中两个向量之间夹角的余弦，余弦越接近于1，则向量的夹角越接近于0，即两个向量越相似，该理论在多维空间中同样适用。

不同径向坐标系数下，±10倍和±20倍景深离焦下的余弦相似性曲线如图7所示，为便于展示曲线细部差异，纵坐标采用差值处理。理论上离焦一致性良好的调制传递函数具有相似的夹角余弦数值，随着径向坐标系数的增大，夹角余弦逐渐变大，不同离焦参量下的夹角余弦差距逐渐缩小并接近1。

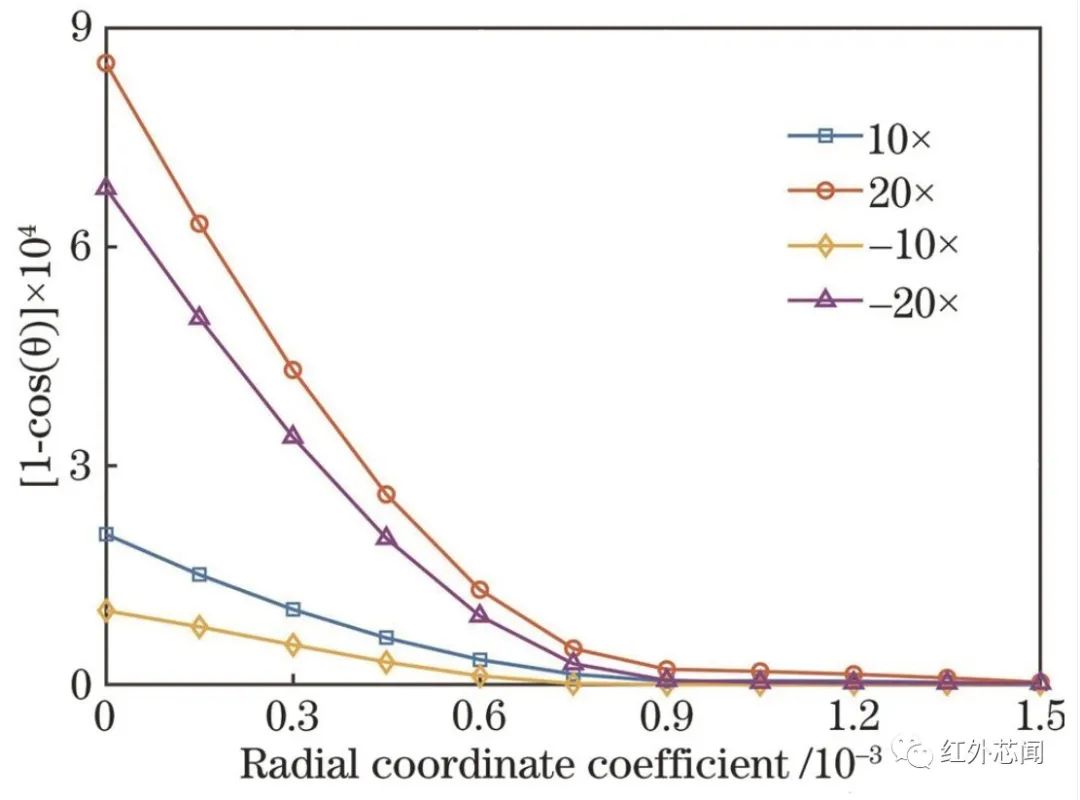
图7 不同离焦状态下的余弦相似性曲线

通过图5~7的分析可知，点扩散函数中心能量取极值时，不同离焦倍率的调制传递函数差异显著，因此径向坐标系数的选择应当在确保调制传递函数一致性的同时，尽可能保证点扩散函数中心能量的集中性。欧氏距离和余弦相似性分析表明，径向坐标系数取1.5×10⁻³时，调制传递函数对离焦脱敏；离散积分分析表明，在此基础上增大径向坐标系数，调制传递函数包围面积进一步减小。

优化后的波前编码系统0°视场角下的三维和二维笛卡儿坐标典型点扩散函数如图8所示，纵坐标表征的点扩散函数强度归一化到100。与脉冲型函数相比，波前编码系统点扩散函数支持域变大，中心点能量相对较高，同时在第四象限集中了大部分能量。第四象限的能量呈三角形分布，以零点坐标为顶点，以水平坐标轴为直角边，点扩散函数强度随着与顶点距离的增加而变小，直角边强度较象限内强度高。考虑光学系统的视场，点扩散函数在边缘视场约有3.5%~7.9%的能量损失。

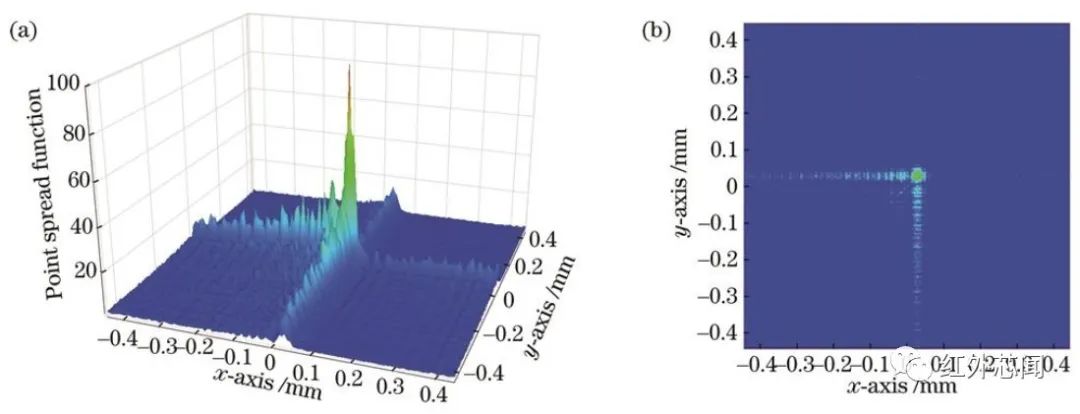
图8 波前编码系统点扩散函数

短波红外波前编码仿真

由于点扩散函数支持域的扩大化，波前编码系统中间图像是对离焦不敏感的模糊图像。模糊图像复原是波前编码应用中的核心问题之一，通常采用低通滤波算法从模糊图像中还原清晰图像。

图9为常规光学系统和波前编码系统在不同离焦量下的成像效果对比图。目标为北方地区冬季室外场景，图像分辨率为640 pixel×512 pixel。由于正向离焦和反向离焦具有相似的成像效果，因此选择0倍、10倍、20倍景深离焦。常规光学系统的成像质量随离焦的增加而恶化，大倍率离焦下调制传递函数零点丢失，导致信息无法还原。由于相位板对波前编码系统光程差的改变，即使在理想焦面位置中间图像仍然模糊，不同倍率离焦下系统具有相似的中间模糊图像，中间模糊图像灰度值差异在-0.071~0.082之间，均方根误差为0.0132。

图9 光学系统离焦效果示意图：（a）（b）（c）常规光学系统；（d）（e）（f）波前编码系统

在波前编码低通滤波反卷积算法中，Lucy-Richardson算法是基于贝叶斯理论的空域图像迭代复原算法，利用期望最大化实现复原图像的最大似然性，适用于处理已知点扩散函数导致的图像模糊。仿真实验中从0倍离焦波前编码系统的0°中心视场对应的图像中选取点扩散函数卷积核，采用Lucy-Richardson经典算法对图像进行还原处理，波前编码系统中间模糊图像复原效果如图10所示。0倍离焦、10倍离焦、20倍离焦复原图像信噪比分别为6.57 dB、6.68 dB、6.66 dB，峰值信噪比分别为26.91 dB、38.50 dB、37.34 dB。统计结果与图10相同，由于点扩散函数支持域的扩大化，点扩散函数中心点附近存在较强的能量起伏，复原图像出现不同程度的振铃现象，在0倍离焦下尤甚，表现为峰值信噪比的降低。

图10 波前编码系统复原图像示意图：（a）0倍离焦；（b）10倍离焦；（c）20倍离焦

结论

将波前编码引入短波红外波段，设计一款60 mm口径、20°视场轻小型短波红外相机，在系统光瞳处添加三次方型硅基相位板扩展景深。遵循调制传递函数一致性和点扩散函数中心点能量集中化两大原则，摆脱常规的单一性评价指标，利用光学软件优化后的相位板参数为1.5×10⁻³。短波红外图像仿真结果表明，至少在±20倍景深范围内，波前编码系统利用Lucy-Richardson经典算法可以从中间模糊图像中还原清晰图像，峰值信噪比高达38.5038 dB。波前编码仅对相位板参数进行优化设计，保留了原始系统的功能完整性，对由离焦引起的成像质量的恶化具有良好的校正作用，对提升载荷的平台适应性和环境适应性具有一定的参考价值，后续可以在此基础上探讨波前编码在初级像差校正和实际应用中的作用。

编辑：黄飞