

基于FPGA的汉明距离电路设计
FPGA/ASIC技术
描述
随着数字化的发展,数字集成电路也得到了广泛应用。20世纪80年代中期,Altera和Xilinx分别推出了类似于PAL结构的扩展型CPLD和与标准门阵列类似的FPGA,它们都具有体系结构和逻辑单元比较灵活、集成度高以及适用范围广等特点。同时,这两种器件也兼容了PLD和通用门阵列的优点,可实现较大规模的电路编程同时也很灵活。
汉明距离在信息论中的定义是两个等长字符串之间的汉明距离,也就是两个字符串对应位置的不同字符的个数。例如:*1011101与1001 001之间的汉明距离就是2;*2143896与2233796之间的汉明距离为3;*“toned”与“roses”之间的汉明距离为3。
在通信中,累计定长二进制字中发生翻转的错误数据位通常也被称为信号距离。事实上,汉明重量分析在包括信息论、编码理论、密码学等领域都有应用。
1 硬件设计
在扩频通信和数字突发通信系统中,接收机进行的数字相关检测或独特码检测,实际上就是本地一组确定序列的一位二进制数,接收机将接收到的数据连续不断的送入N位移位寄存器中,这样,任一瞬间移位寄存器中的内容即为一串二进制码,移位寄存器的输出作为ROM的地址输入,这样,经查找表运算后,ROM就可输出所需的数据,并将所得数据送入汉明计算电路以得到汉明距离,再经过门限判决输入的汉明距离。其汉明距离的计算电路框图如图1所示。

1.1 8位并入串出移位寄存器
图2是本系统中的并入串出移位寄存器电路图。图2中,当移位/置入控制端(
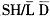
)为低时,并行数据(A—H)被置入寄存器;而当
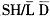
为高电平时,并行置数功能被禁止。当CLK和CLK INK有一个为低电平且
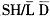
为高电平时,另一个时钟则可以输入;当CLK和CLK INK有一个为高电平时,另一个时钟被禁止:而只有在CLK为高电平时,CLK INK才可变为高电平。

1.2 ROM查找表的设计
用FPGA设计汉明距离电路的另一个关键是存储器ROM,图3所示是一个lpm_rom的器件图。设计时,移位寄存器的输出作为ROM的地址输入,这样,经查找表运算后,ROM就可以输出所需的汉明数据。

1.3 逻辑计算电路
图4所示是本系统中的逻辑计算电路的c5in3out的器件图。通过c5in3out可计算出序列D6~D32的汉明距离。序列D0~D5(即图4中的A,B,C,D,E)的汉明距离可以采用逻辑函数获得。逻辑计算电路有三个二进制输出变量,由最高有效位到最低有效位依次为A、B、C(即图4中的X,Y,Z),其逻辑表达式为:


1.4 汉明加法器
图5所示是一个汉明加法器的add器件图。add通常是采用求和网络法求和。求和网络法将ROM输出的数据两两通过一个加法器相加后,可将得出的结果再两两通过一个加法器相加,依次将各项计算结果相加在一起,其最终的累加结果便是汉明距离。

2 汉明电路的仿真调试
2.1 8位并入串出移位寄存器的max+pluslI仿真
8位并入串出移位寄存器max+plusII波形仿真如图6所示。其中的Clk为移位时钟信号;Load为并行数据预置使能信号;Din是8位二进制并行预置数据端口;Qb表示当前值reg(0)向qb输出;Reg(8)为当前值和移位值(如:9A 1001 1010B;移位后:4D 0100 1101 B:第二次移位:A6 10100110 B)。

2.2 32位序列汉明距离电路的实现仿真
选取查找表-求和网络法来实现32位汉明距离的计算时,可分别将(D6~D14)、 (D15~D23)、(D24~D32)作为查找表的地址线,再由此计算出序列D6~D32的汉明距离。而其序列D0~D5的汉明距离可以采用逻辑函数获得,具体的波形仿真如图7所示。
图7中,Datain[31..0]为汉明距离电路的输入端口;Out[4..0]为汉明距离计算输出端口(内置的32位数可用十六进制表示为000000 00)。例如F800A08C即1111 1000 0000 0000 1010 0000 10001100B,输出的汉明距离d为10。
3 结束语
设计完成后,可使用FPGA(即现场可编程门阵列)进行下载验证,FPGA是专用集成电路(ASIC)领域中的一种半定制电路,FPGA既可解决定制电路的不足,又可克服原有可编程器件门电路数有限的缺点。而使用Max+PlusⅡ软件和VHDL语言进行电路设计,不仅可以进行逻辑仿真,还可以进行时序仿真。由于本设计在编写过程中使用了较多的与门和异或门,所以,在波形仿真图中,波形显示具有比较长的延时。但是,自行编写的计数器功能完善,程序简单明了,完全可以实现32位汉明距离的计算。
-
FPGA CPLD数字电路设计经验分享.2021-09-18 1307
-
吴汉明:国内集成电路产业化推进还有差距2020-10-15 2633
-
FPGA的硬件电路设计教程和FPGA平台资料简介2020-07-06 2082
-
FPGA的原理及电路设计应用的讲解2019-08-06 3832
-
电路设计[FPGA]设计经验分享2019-01-03 2801
-
如何使用汉明距离分类算法达到精准营销2018-11-19 1213
-
基于汉明距离的改进粒子群算法2017-11-24 819
-
DSP和FPGA的HDLC协议通讯电路设计2017-10-19 1125
-
基于FPGA的串口通信电路设计2017-01-24 822
-
基于FPGA的惯性平台测试保护电路设计2016-01-04 551
-
电路设计[FPGA]设计经验2012-05-23 7396
-
什么是汉明距离?2011-08-11 3996
-
非相干扩频测控系统距离模拟电路设计2010-01-13 507
全部0条评论

快来发表一下你的评论吧 !

