经典的滤波算法：Madgwick滤波算法

前言

之前的一次推送介绍了Mahony姿态解算算法（IMU姿态滤波算法——Mahony算法：原理与代码），这次介绍另一个经典的滤波算法：Madgwick滤波。

Madgwick滤波算法根据加速度计、陀螺仪、以及磁力计，融合计算机体四元数，计算速度快、精度较高。本文详细介绍六轴融合，即根据加速度计和陀螺仪数据，计算IMU的姿态。

 

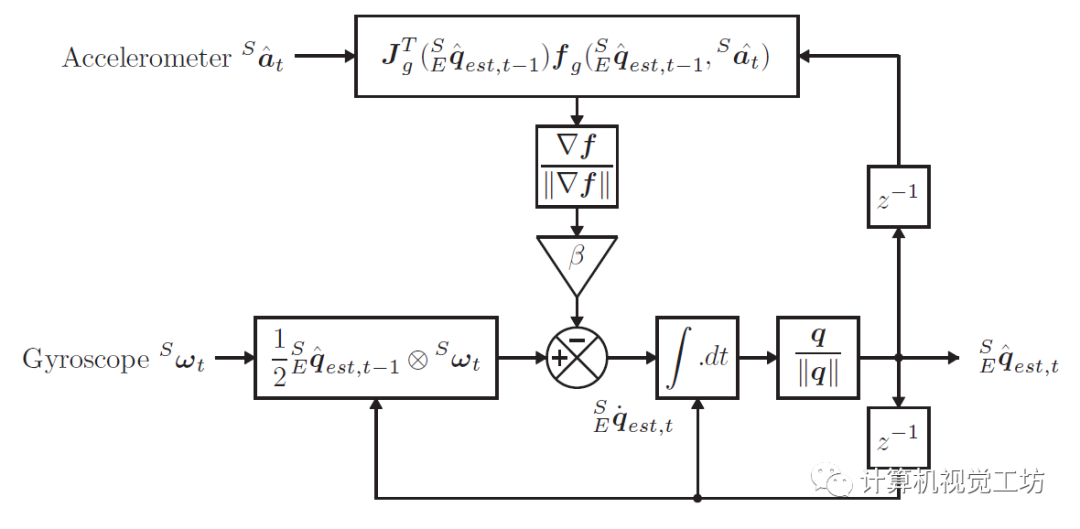
算法

2.1 重力方向对齐优化

首先要指出的是，Madgwick算法假设加速度计测量的加速度完全由重力提供，即物体本体运动产生的加速度可忽略不计。这一点和Mahony算法是一样的。

假设world系中一个向量在world下的表示为 ，在传感器下的观测为 ，传感器位姿以四元数表示记为 。如果此时的姿态是准确的，应该有：

然而由于姿态不准，等式并不成立。因此，我们定义目标函数：

令目标函数取到0（在四元数对应的参数空间上），则得到了最优的姿态，即。这可以当作一个优化问题进行求解。而优化问题的求解思路之一，就是采用梯度下降法。记的梯度为，那么在迭代优化求解时，下一次取值应该为当前取值减去当前梯度方向走一个步长，即

其中，

其中， 为 的雅可比（具体的形式可参考文献[1][2]）。

可以将步长 视作加速度计产生的数据对姿态的收敛速度，同时考虑到角速度在当前时刻会产生一个角速度的增量，因此加速度这部分的收敛必须大于角速度变化速率，即 ，其中 。

对于一般的优化，我们需要不断迭代求解直到收敛，但Madgwick为了保证算法的实时性，只进行一次梯度下降，也能取得差不多的精度。

具体地，如果我们把world系下的这个向量 取重力 ，姿态传感器对应的测量 即为IMU的加速度计读数 ，此时有：

2.2 角速度融合

另一方面，我们可以通过角速度计提供的角速度积分，得到姿态，即：

这里我们对四元数进一步的区分。我们对上一时刻滤波后的姿态（四元数）记为 ，当前时刻角速度计的读数即角速度为 ，角速度计计算得到的姿态为 。

对2.1中优化后得到的四元数记为 ，即加速度计计算得到的姿态。

那么，当前时刻估计的姿态取做两个姿态的加权平均：

至于 如何取值，下一小节进行讨论。

2.3 权重取值

由于角速度存在漂移，我们定义角速度的发散速率为 。这里如果加速度计对姿态贡献的收敛速度，等于角速度的发散速度，则由式(5)融合的结果依旧是准确的姿态。即需要有：

即

由于 中对 没有限制，因此取 为无限大，此时，综合(1)(5)(6)，有：

定义估计的角速度 ，则最终有：

再看式(7)，可以将视作，下一时刻的姿态，等于上一时刻姿态，加上角速度计的积分，减去一个与角速度计噪声水平 相关的增量，这个增量的与加速度计的优化时的梯度有关。最终，Madgwick滤波算法的参数只有一个。

代码

Matlab完整代码[3]如下：

function obj = UpdateIMU(obj, Gyroscope, Accelerometer)

    q = obj.Quaternion;

    if(norm(Accelerometer) == 0), return; end
    Accelerometer = Accelerometer / norm(Accelerometer); % 归一化加速度计数据

    % 式(2)和(3)
    F = [2*(q(2)*q(4) - q(1)*q(3)) - Accelerometer(1)
        2*(q(1)*q(2) + q(3)*q(4)) - Accelerometer(2)
        2*(0.5 - q(2)^2 - q(3)^2) - Accelerometer(3)];
    J = [-2*q(3), 2*q(4),    -2*q(1), 2*q(2)
        2*q(2),     2*q(1),     2*q(4), 2*q(3)
        0,         -4*q(2),    -4*q(3), 0    ];
    step = (J'*F);  
    step = step / norm(step); % 式(1)中的减号后面的部分，即修正量

    % 式(8)中的修正角速度
    qDot = 0.5 * quaternProd(q, [0 Gyroscope(1) Gyroscope(2) Gyroscope(3)]) - obj.Beta * step';     

    % 式(7)(8)，即迭代到下一步。
    q = q + qDot * obj.SamplePeriod;
    obj.Quaternion = q / norm(q); % normalise quaternion
end

与Mahony算法的比较

Madgwick算法与Mahony算法相比，最大的不同之处是如何对待加速度计估计的误差。Mahony是利用叉乘，Madgwick是利用优化；

Mahony可以视作一个PI（比例-积分）控制器，Madgwick是一个P（比例）控制器；

Madgwick比Mahony的精度稍高一丢丢，但Mahony的计算速度略快[4]；

Mahony与Madgwick都需要假设加速度测的只是重力，因此在加速度变化剧烈情况下表现不佳。

编辑：黄飞