最全超单元静力学、拓扑优化、模态、振动、传递路径TPA和动刚度分析等

导读：超单元一个最有意义的用处便是大幅降低计算花费，提升分析效率。利用有限的计算资源完成计算更为庞大的分析。超单元可以大幅降低整体模型的自由度，所以计算量相对更低，可以用来做一些更为复杂的分析。近日，笔者在仿真秀原创独家首发的视频教程《超单元法在产品开发仿真应用17讲-静力学/拓扑优化/模态/随机振动/传递路径TPA和动力学分析》，希望对工程师朋友学习超单元法有些许帮助，如有不当，欢迎批评指正，详情见后文 。

       一、超单元方法的定义及分析

什么是超单元法，什么是超单元？

在一个整体模型中，切割出部分模型(关注区域)，将切割的区域模型通过模态、矩阵或传递函数等进行表示，同时提取出相应的矩阵或参数，这一过程称为超单元生成（缩聚）。然后在对整体模型进行分析，此时的整体模型包括生成的超单元模型和剩余的部分模型（也称为残余模型），超单元模型即用这些“表示”来替换切割出来的部分模型；进而将此两部分模型组合成整体模型进行相应的工况分析。

这样的一种操作方法或建模方法，我们称之为超单元法，或者叫直接矩阵输入法；这些“表示”即为所谓的超单元。而整体模型除去超单元的部分称为残余结构（剩余结构）。将超单元与残余结构组合进行求解，得到相应的工况结果。换句话讲，即将一个规模较大的模型分解成动态变化部分（或剩余模型）和固定部分（即超单元模型），此时进行整体的求解时可极大的缩短求解时间，进而提升分析效率，可以在有限的时间内做更多的优化分析研究。

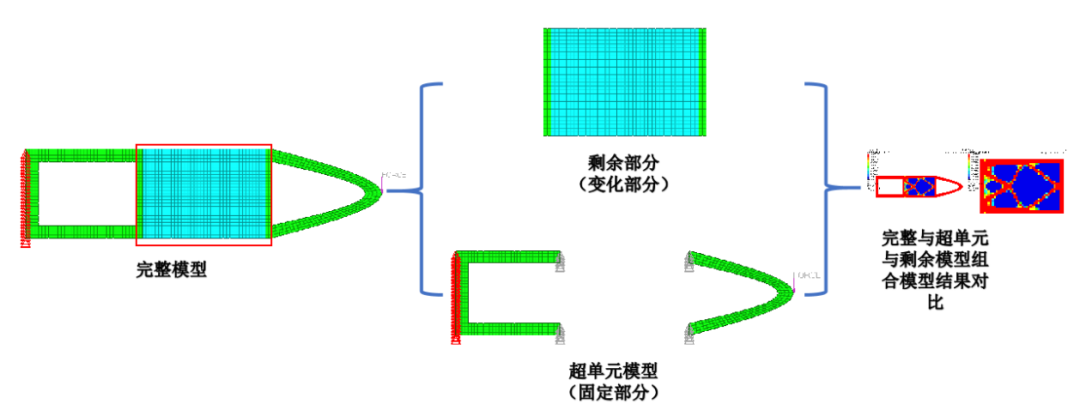
图1 超单元模型的分解及分析

二、超单元方法的意义

为什么要采用超单元法？

1、大幅度降低计算时间、提升分析效率

无论是采用哪种超单元，相比于没有超单元的直接有限元计算方法，整体模型的分析速度及求解效率都能得到大幅提升。

2、利用有限的计算资源完成大规模分析

超单元可以大幅度降低整体模型的自由度，所以计算量相对更低，可以用来做一些更为复杂的分析。同时可以在有限的时间内做更多的study。

3、避免模型错误带来的额外风险

整体模型中出现错误，需要对整个模型进行重新处理。但是如果超单元出现问题，仅需要对超单元进行修改。

4、实现模块化处理

每个超单元都需要单独切割出现进行独立的处理，所以可以实现模型的模块化。

5、实现模型的保密

因为超单元不显示具体的信息，仅仅是矩阵或参数表征，所以如果模型可以实现关键信息的保密。

6、平台化

可以实现不同模型之间的平台化，通用化等

三、超单元的基本理论

1、超单元的动力学方法

对于超单元来讲，其动力学方程可以写成以下形式。

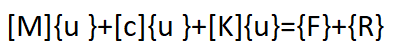    （1）

将该方程的自由度通常分为两部分，即超单元内部自由度及界面（或连接）自由度。则进一步可以将方法（1）分解为以下形式：

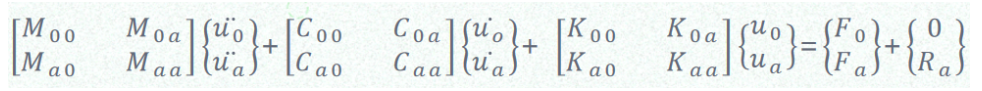
（2）

其中，{u_0}为内部自由度；{u_a}为外部自由度，将（2）式展开可以得到：

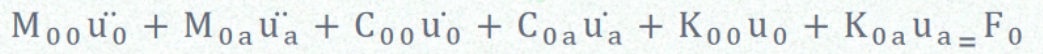
(3)

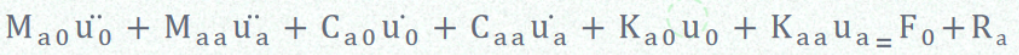
（4）

对于静力学问题，所有的[M]和[c]矩阵均为0，即方程（3）可以简化为：

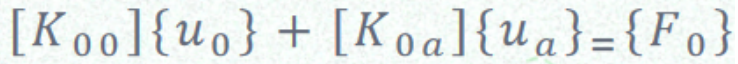
  (5)

可以用{ua}表示{u0}为：  

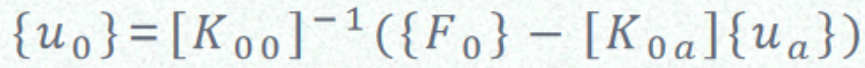
 (6)

将（6）代入（4），可得到：

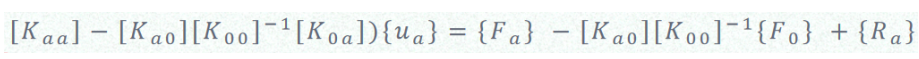
 （7）

即将{Ua}前部分采用[Kaa∗]表示，等号右边第一项采用[Fa∗]表示，即方程（7）可以表示如下：

[Kaa∗]{ua}=[Fa∗]+{Ra} （8）

各超单元的{ua}是整个结构的残余结构的分析自由度{uA}的一部分。可以按照一般单元装配成总体矩阵相同的方式，由各超单元的边界矩阵装配得到残余结构的矩阵。然后求解出{uA}，再回到各超单元进行数据恢复，先从{uA}中分出{ua}，再由方程（5）得到超单元的{u0}与{ua}一起构成超单元的完整自由度集。

三、超单元方法的实际应用

在采用超单元方法的使用前，我们首先要理解为什么要采用超单元，在超单元方法的意义中可以发现，超单元理论上讲可以应用于一切模型的计算中；但更为通俗的理解，其主要是应用于大模型（如百万级甚至千万级的模型求解中），同时也是考虑到实际计算资源的有限情况下。例如在实际中可以应用在整车开发中的整车级工况分析，以及系统级的分析模型，以及新能源产品的开发中（如储能、动力电池等）。

图2 某车型整车模型（百万级规模）

超单元的应用中，需要首先理解超单元的缩聚方法及缩聚流程，同时对于不同的方法有不同的设置要求，如对于静力学缩聚通常可以采用直接矩阵输入法及动力缩聚方法，不同的方法其应用的场景有所区别。同时要准确定义超单元界面，此时就需要准确理解界面定义的详细关键字的使用方法。

1、超单元实战之一，在静力学缩聚的应用，对于一个近七百级规模的模型，采用不同的超单元方法，其计算结果及求解时间对比如下：

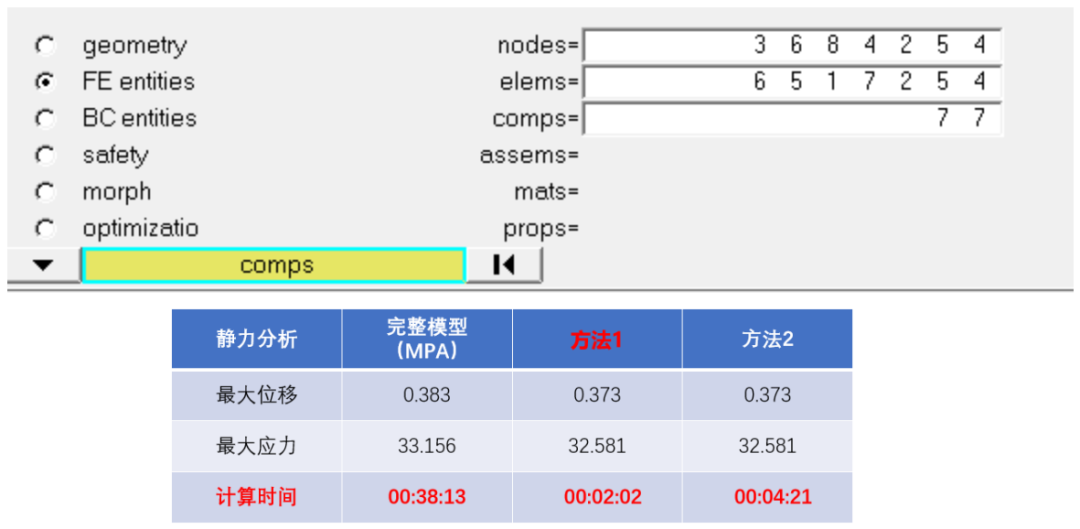
图3 某七百级模型采用不同超单元结果对比

2、超单元实战之二，在整车传递路径分析的应用，对于一个近五百万级规模的模型，采用不同的超单元方法，其计算结果如下，其计算时间由基础的近三小时缩短为近五分钟。

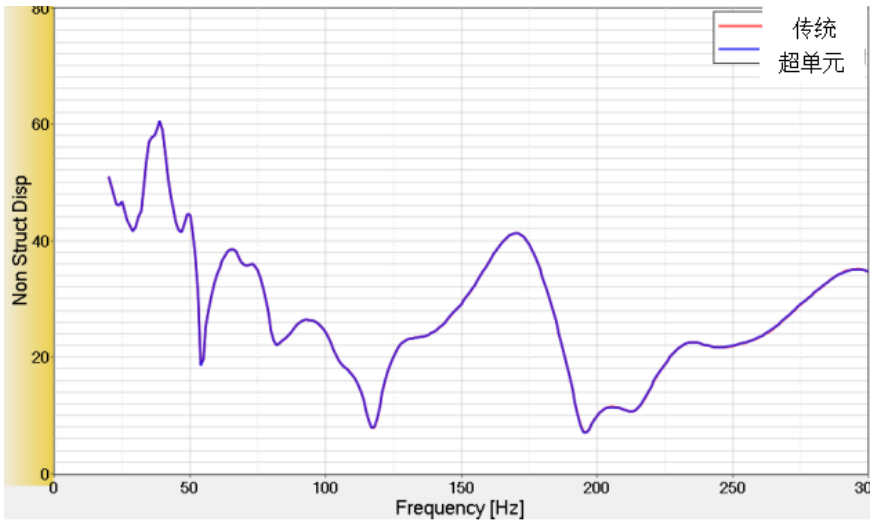
图4 整车动力总成响应分析结果

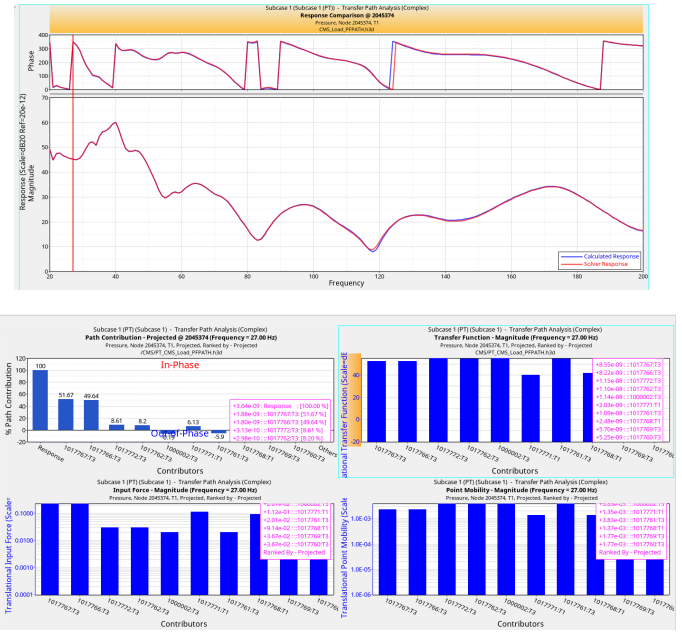
图5 整车动力总成传递路径分析结果

审核编辑 ：李倩