

电池效率的预测模型建立
电子说
描述
数学定义Contact Selectivity
接触区域少数载流子复合电流密度为
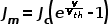 ----(1)
----(1)
J m ,在电压V时接触区域少数载流子电流密度;
J c ,接触区域复合电流密度因子, 单位A/cm ^2^ ;
V th , thermal voltage热电压, 25oC时为25.7mV;
少数载流子电阻可定义为V/J m ,但由于电池电压取决于接触特性外很多其它电池特性,其不太适合作为分析接触特性的参数。因此,作者使用零电压下电流-电压曲线的反斜率作为少数载流子的特征电阻率ρm的表征:
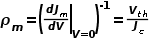 ----(2)
----(2)
假设接触区域多数载流子具有线性的电流-电压特征,即J M =V/ρ c ,则接触区域多数载流子 电阻率ρM有:
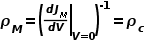 ----(3)
----(3)
ρ c ,接触区域的接触电阻率,单位Ωcm ^2^ ;
需要注意的是,作者选择零电压作为参考点是任意的,也可以选择任何其它任何电压,例如最大功率点电压V mpp ,此时得到的Contact Selectivity会低一个常数倍e ^Vmpp/Vth^ ,但最终推导出的所有物理结论保持不变。因此,由于不同电池最大功率电电压Vmpp不同,因此选择V=0是最简单的选择。
现在可以用多数载流子和少数载流子电阻率定于接触区域载流子选择性:
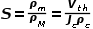 ----(4)
----(4)
另外,由于S数量级太大,定义对数标称S 10 :
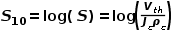 ----(5)
----(5)
非理想选择性接触的电压-电流曲线
下图为仅由单个选择性接触构成的太阳电池等效电路,包含三个组成部分:
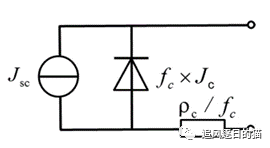
(i) 恒流源,本文以110μm厚度硅片为例,假设Lambertian陷光,在AM1.5G光谱0.1 W/cm^2^ 条件下,仅考虑本征复合时,电流密度Jsc=43.6 mA/cm ^2^ ;
(ii) 二极管,表征接触区域的复合,复合电流密度为式(1)定义的J c ;
(iii) 串联电阻,表征接触区域接触电阻,电阻率大小为式(2)中定义的ρ c ;
在不考虑其它因素的条件下,以上表征的等效电路满足下式:
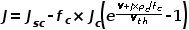 ----(6)
----(6)
V,太阳电池外电路电压;
作者将(ρ c /f c ,f c ×J c )定义为有效器件的接触电阻率与接触复合电流密度,即根据金属接触比例对(ρ c , J c )进行归一化处理,此时根据最大功率点V mpp ×J(V mpp )/(0.1W/cm2)获得的效率即为部分金属接触(接触比例f c )时太阳电池的理论效率。
而其中存在一个最优的金属接触比例f c,max ,该参数下对应接触选择性参数为(ρ c /f c,max ,f c,max ×J c ),具有最大的接触选择性S10以及最高的器件理论效率。
文章进一步推导出fc,max的计算方案:
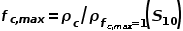 ----(7)
----(7)
式中, 为S
为S10的函数,可由以下经验公式进行计算。
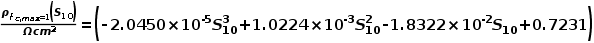 ----(8)
----(8)
当同时考虑正负极接触时最优接触比例
文章进一步讨论同时考虑太阳电池背场(bsf)和发射极(emitter)接触时对应的选择性及最优接触比例的计算。同时考虑太阳电池bsf和emitter的器件综合接触选择性可由下式计算:
 ----(9)
----(9)
(9)式对应方程在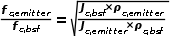 ----(10)
----(10)
时,对应的S10,bsf&emitter达到最大值,为
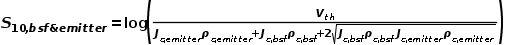 ----(11)
----(11)
而器件最优金属接触比例需要同时考虑bsf和emitter接触,满足类似式(7)的变体,如下式:
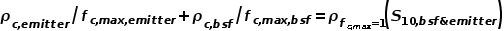 ----(12)
----(12)
而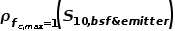 的计算仍满足式(8),但其中单接触选择性S
的计算仍满足式(8),但其中单接触选择性S10被综合接触选择性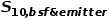 所取代。
所取代。
最后,由式(10)与式(12)即可解出bsf与emitter分别对应的最优接触分数fc,max,bsf和f c,max,emitter 。
接触选择性与太阳电池效率
文章根据假设条件,针对式(6)数值求解得到如下效率与接触选择性的关系:
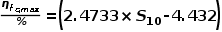 ----(12)
----(12)
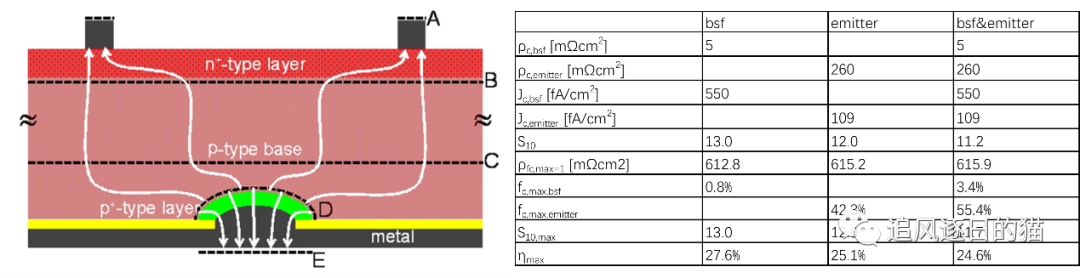
以文中给出案例中较为简单的PERC(PERC电池结构如下左图所示)案例为例,在不考虑硅片本身复合,110um厚度前提下,已知接触区域复合电流密度及接触电阻参数ρ c ,bsf , J 0,bsf , ρ c,emitter , J0,emitter条件下,根据上述模型可计算出电池最优效率以及对应的接触比例设计,计算结果如下右表所示,其中‘bsf’及‘emitter’两列为仅考虑单独背场(bsf)或发射极(emitter)接触条件下对应的计算结果,’bsf&emitter’为同时考虑背场(bsf)和发射极(emitter)接触的计算结果。计算显示了这种电池结构的效率上限以及接触设计优化方案。
-
经济预测模型2011-08-15 2197
-
参照光伏电池的物理模型,可建立用于实现其仿真的matlab...2013-10-26 4866
-
动力电池循环寿命预测方法研究(资料下载)2016-01-07 4578
-
Keras之ML~P:基于Keras中建立的回归预测的神经网络模型2018-12-20 4357
-
基于Keras中建立的简单的二分类问题的神经网络模型(根据200个数据样本预测新的5+1个样本)—类别预测2018-12-24 5575
-
PaddlePaddle使用预测模型预测图片报错及解决方法2019-05-31 2341
-
模型预测控制+逻辑控制2021-08-17 1794
-
模型预测控制介绍2021-08-18 2640
-
什么是MPC模型预测控制?2021-11-22 3780
-
自回归滞后模型进行多变量时间序列预测案例分享2022-11-30 2668
-
基于排队论的作战效能预测模型2017-12-26 1023
-
基于FSVM建立含氧量预测模型2018-01-12 876
-
如何使用改进GM模型进行房价预测模型资料说明2018-12-19 1875
-
锂电池多状态模型剩余寿命预测方法2021-05-31 1139
-
如何利用高斯过程回归模型建立燃料电池电堆功率预测模型?2023-11-02 2544
全部0条评论

快来发表一下你的评论吧 !

