

滤波器介绍及系数设计
描述
在数字信号处理领域中,数字滤波器占有非常重要的地位。根据其计算方式可以分为FIR(有限脉冲响应)滤波器,和IIR(无限脉冲响应)滤波器两种。
FIR滤波器根据如下公式进行计算:
y[m] = b[0]x[m] + b[1]x[m-1] + …. + b[p]x[m-p]
IIR滤波器:
y[m] = b[0]x[m] + b[1]x[m-1] + …. + b[p]x[m-p]
-a[1]y[m-1] – a2y[m-2]- … - a[Q]y[m-Q]
FIR滤波器:时刻m的输出y[m]由时刻m的输入x[m]以及之前的输入x[m-1] ... x[m-P]和滤波器的系数b[0] ... b[P]求乘积和.
IIR滤波器再减去之前的输出y[m-1] ... y[m-Q]和系数a[1] ... a[m-Q]的乘积和.
FIR滤波器是IIR滤波器的一种特殊情况.
滤波器的作用:改变信号频谱,实现频域滤波。
低通滤波器参数特征:
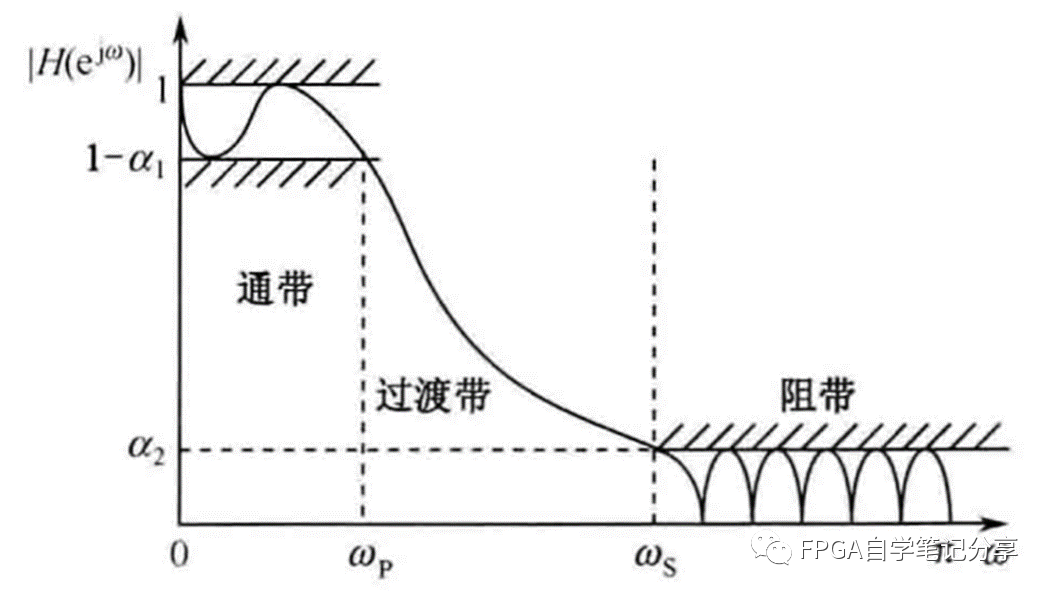
比如,设计一个归一化为0.2通带的低通滤波器,其频谱响应为:

生成一个随机信号将其作为输入经过上述滤波器,结果如下,蓝线是随机信号的频谱,橙线为经过滤波器后的频谱。

再比如一个双音信号,经过该滤波器,输入信号频谱:

经过滤波器滤波后的频谱:

数字滤波器的设计,最常用的是MATLAB的 filterDesigner工具根据需求直接配置参数,即可生成滤波器系数,同时给出滤波器的频谱响应,使用特别方便:

使用python的话可以用scipy库的signal.remez函数:
import scipy.signal as signal
signal.remez(numtaps, bands, desired,
weight=None, Hz=1, type='bandpass', maxiter=25, grid_density=16)
其中:
numtaps : 所设计的FIR滤波器的长度
bands :一个递增序列,它包括频率响应中的所有频带的边界,其值在0到Hz/2之间,如果参数Hz为缺省值1的话,那么可以把它当作是以取样频率正规化的频率
desired : 长度为bands的一半的增益序列,它给出频率响应在bands中的每个频带的增益值
weight : 长度和desired一样的权重序列,它给出desired中的每个增益所占的权重,即给出desired中的每个增益的重要性,值越大表示其越重要
type : 'bandpass'或者'differentiator'
比如设计一个归一化为0.1的低通滤波器,截止频率0.11,系数长度701的滤波器:
len_h=701
bands = np.array([0., 0.1, .11, .5])
h = signal.remez(len_h, bands, [1,0], [100,1])
滤波器的频谱响应为:

-
AFE032系数滤波器的设置格式是什么,如何设置?2024-09-04 378
-
低通滤波器、高通滤波器、带通滤波器的简单介绍2024-07-09 41090
-
滤波器的类型介绍2024-05-21 2973
-
Matlab生成fir滤波器抽头系数的流程2024-03-25 2871
-
FIR滤波器系数2021-08-17 1410
-
怎样去计算滤波器的系数2021-07-14 1290
-
数字滤波器-IIR滤波器原理介绍&Verilog HDL设计2020-09-27 6820
-
系统函数的系数和滤波器参数之间的关系2019-03-13 3085
-
AD7762滤波器系数配置问题2018-12-18 1814
-
过采样技术中的低通滤波器,可变参数低通滤波器的设计2018-10-26 9938
-
如何设计低通FIR滤波器2018-08-23 5968
-
巴特沃斯滤波器的原理_巴特沃斯滤波器优点介绍2018-01-26 51952
-
晶体滤波器、陶瓷滤波器和声表面滤波器的介绍2017-11-10 5352
全部0条评论

快来发表一下你的评论吧 !

