

基2FFT的verilog代码实现及仿真
描述
上文基2FFT的算法推导及python仿真推导了基2FFT的公式,并通过python做了算法验证,本文使用verilog实现8点基2FFT的代码。
根据算法推导,8点FFT的verilog代码整体结构为:
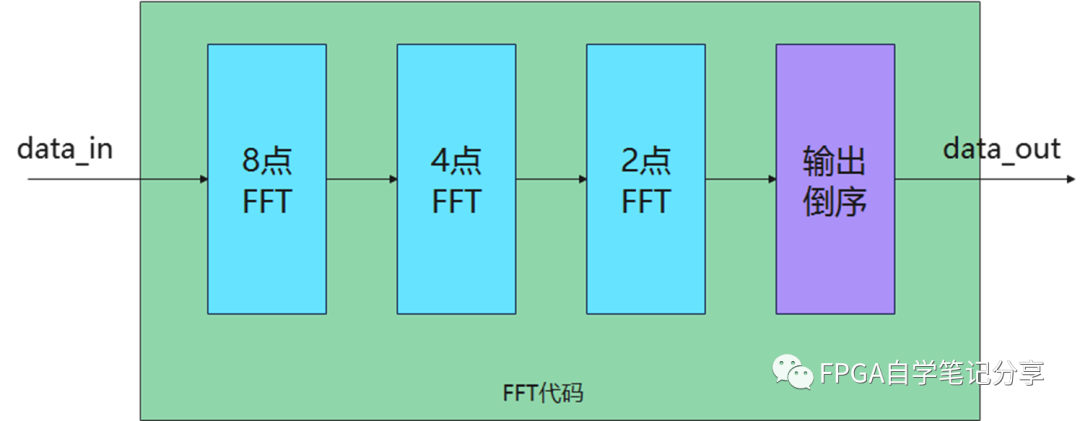
verilog代码实现首先进行2点FFT的实现,代码主要做D0+D1操作和(D0+D1)*W02操作,代码及操作内容如下:
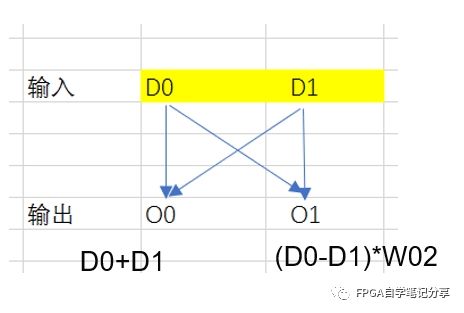
// ============================================================
// File Name: cm_fft2_N2
// VERSION : V1.0
// DATA : 2023/1/1
// Author : FPGA干货分享
// ============================================================
// 功能:基2FFT N=2的数据处理
// delay : 2clk
// ============================================================
`timescale 1ns/100ps
module cm_fft2_N2 #(
parameter C_DATA_WITH = 16 )
(
input wire I_sys_clk , /// 工作时钟 100M
input wire I_data_start , /// 数据开始进入标志,与第一个数据对齐输入
input wire [C_DATA_WITH-1:0] I_data_in_real , /// 数据输入,从start开始连续输入
input wire [C_DATA_WITH-1:0] I_data_in_imag , /// 数据输入,从start开始连续输入
output reg O_data_start , /// 数据开始输出标志与第一个数据对齐输出
output reg [C_DATA_WITH:0] O_data_out_real , /// 数据输出,从start开始连续输出
output reg [C_DATA_WITH:0] O_data_out_imag /// 数据输出,从start开始连续输出
);
// ============================================================
// 内部参数
// ============================================================
/// W02=1
// ============================================================
// 变量
// ============================================================
reg S_data_start ;
reg [C_DATA_WITH-1:0] S_data_in_real_d1 ;
reg [C_DATA_WITH-1:0] S_data_in_real_d2 ;
reg [C_DATA_WITH-1:0] S_data_in_imag_d1 ;
reg [C_DATA_WITH-1:0] S_data_in_imag_d2 ;
// ============================================================
// main code
// ============================================================
always @(posedge I_sys_clk)
begin
S_data_start <= I_data_start ;
O_data_start <= S_data_start ;
end
/// 缓存第一个数
always @(posedge I_sys_clk)
begin
S_data_in_real_d1 <= I_data_in_real ;
S_data_in_real_d2 <= S_data_in_real_d1 ;
S_data_in_imag_d1 <= I_data_in_imag ;
S_data_in_imag_d2 <= S_data_in_imag_d1 ;
end
always @(posedge I_sys_clk)
if(S_data_start)
/// x(n)+x(n+N/2)
begin
O_data_out_real <= {S_data_in_real_d1[C_DATA_WITH-1],S_data_in_real_d1} + {I_data_in_real[C_DATA_WITH-1],I_data_in_real} ;
O_data_out_imag <= {S_data_in_imag_d1[C_DATA_WITH-1],S_data_in_imag_d1} + {I_data_in_imag[C_DATA_WITH-1],I_data_in_imag} ;
end
else if(O_data_start)
/// [x(n)-x(n+N/2)]C_W02
begin
O_data_out_real <= {S_data_in_real_d2[C_DATA_WITH-1],S_data_in_real_d2} - {S_data_in_real_d1[C_DATA_WITH-1],S_data_in_real_d1} ;
O_data_out_imag <= {S_data_in_imag_d2[C_DATA_WITH-1],S_data_in_imag_d2} - {S_data_in_imag_d1[C_DATA_WITH-1],S_data_in_imag_d1} ;
end
else
begin
O_data_out_real <= 'd0;
O_data_out_imag <= 'd0;
end
endmodule
