如何把50Hz工频干扰定点清除

01引言

如果单纯依靠模拟电路，是不可能将50Hz干扰彻底抑制掉的，所以这时候就体现出数字信号处理的优越性了。

数字信号处理里面的滤波器分两种:一种是IIR滤波器，另一种是FIR滤波器，本质区别就是IIR滤波器的当前输出与以前的输出和输入有关，FIR滤波器只与输入有关,看一下差分方程就一目了然了。

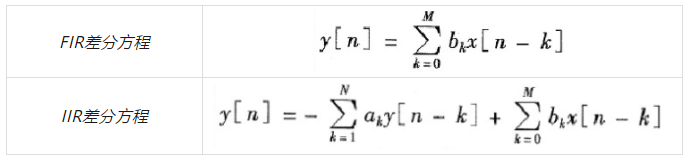
来看一下海宁滤波器的结构和传递函数，

很明显这是一个FIR滤波器，因为输出只与输入有关。而它的滤波器系数也非常好记（1/4）*[1 2 1]=[0.25 0.5 0.25]，这个数值运算量非常小，把它放到单片机里面使用也是毫无压力的，因为，不论是1/4还是1/2都可以在程序中用移位>>运算来实现。

02matlab滤波器设计

废话少说，接下来进入正题， 1Hz信号里面混有较强的50Hz和178Hz干扰，观察图形看一下是这样的。

利用MATLAB的fdatool工具来设计一个能够兼具低通和50Hz陷波功能的滤波器。

参数设置为：FIR滤波，低通，10阶，通带截止频率4Hz，阻带截止频率46Hz，采样率400Hz,生成的幅度响应曲线中虚线是未进行量化后的曲线，可以发现，阻带的衰减幅度最小也有25db，50Hz的衰减频率则达到了70db，

观察下滤波器的参数

未量化的浮点数据还是比较长的，但是效果是最好的，量化后的数据会比较短，具体长度是我们自己设置的，量化的目的是降低运算量，但是以牺牲滤波效果为代价的，我们先把数据导出来进行验证。

在matlab里面进行验证，代码如下

Ts=0.0025;%采样率400hz
len=500; > > n=0:len-1;
%3种频率的信号混合
 x=0.1*sin(2*pi*1*n*Ts)+sin(2*pi*50*n*Ts)+0.5*sin(2*pi*178*n*Ts);
CO=[0.04675 0.05845 0.084 0.1068 0.1225 0.1282 0.1225 0.1068 0.084 0.05845 0.04675];
W=[0 0 0 0 0 0 0 0 0 0 0];
for i = 1:len
W(1) = x(i);
y(i) = W(1)*CO(1)+W(2)*CO(2)+W(3)*CO(3)+W(4)*CO(4)+W(5)*CO(5)+W(6)*CO(6)+W(7)*CO(7)+W(8)*CO(8)+W(9)*CO(9)+W(10)*CO(10)+W(11)*CO(11);
W(11)=W(10);
W(10)=W(9);
W(9)=W(8);
W(8)=W(7);
W(7)=W(6);
W(6)=W(5);
W(5)=W(4);
W(4)=W(3);
W(3)=W(2);
W(2)=W(1);
end
subplot(211);
plot(x);
subplot(212);
plot(y)
axis([0 500, -1.5, 1.5]);

结果如下图：

由于1Hz的信号幅值较低，所以所以看起来会有点小，但是50Hz和178Hz已经消失不见了，但是这个滤波器存在一个问题，就是阶数有点高--10阶，然后浮点运算太多了，在单片机上运行是个负担，所以还得改进一下。

0350Hz精准陷波

这次只定点滤除50Hz信号，实际上通过上面的操作大家应该清楚了，不同的滤波器不过是在调整滤波器的系数而已，那么我们不妨直接来通过修改系数的方式设计滤波器，matlab也提供了这样的功能，见下图：

这里面的系数B=[ 0.125 0.53 -0.75 0.53 0.125];是我反复调整得到的，未量化时是精准的50Hz陷波，量化后会有偏移，如果单片机运算能力尚可的话，就不要量化了，因为本身这里浮点的数据并不长，不多说了，代码与上面没有太大差异，故省略，直接看效果吧。

04结语

实际上阶数还可以继续降低，比如这篇文献里面设计的陷波器就只有4阶，他的采样率是200Hz。

可以发现，数字滤波不过是各种乘加运算，只不过系数不同，滤波的效果和功能也不同。

至于IIR滤波器，实际上设计的方法与上面相差也不大，matlab的代码也与C语言极为相似，如何转化，也不再赘述了。