

板材为啥用介电常数和损耗角正切来表征呢?
描述
作为一个射频工程师,对PCB板材,那肯定是熟悉的不得了。
自从微带电路被发明后,基本上大多数系统,都是以PCB板材作为载体,而各种器件被置于PCB板材上面,发挥各自的性能。
假设射频工程师,选定某种板材时,最关注板材的哪两个参数呢?很显然,就是相对介电常数和损耗角正切。
随便找一个板材的datasheet,比如说在微波频率时,很受欢迎的rogers他们家的 RO4000系列的板材。
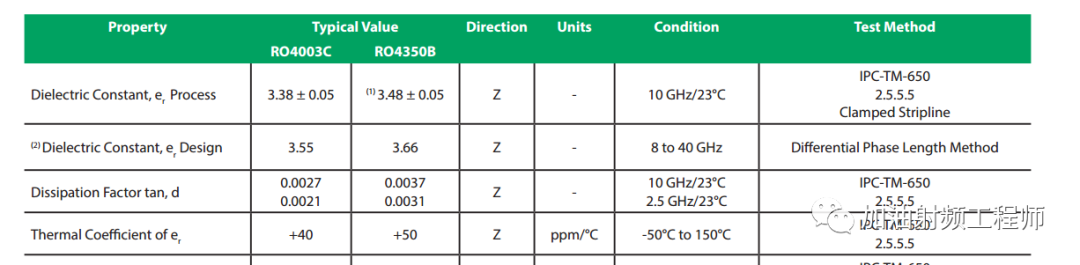
排在前面的,就是介电常数(dielectric Constant)和Dissipation Factor(耗散因子,即损耗角正切)。
可是为啥这两个参数,基本上就能确定这个板材的射频性能呢?
这个嘛,也可以从麦克斯韦方程中找到答案。
麦克斯韦方程,是由麦克斯韦在1873年提出来的。1873年,距现在已经有150年。但现在我们还是在时不时的提起它,用到它。
从这方面来看,学射频也有一个好处,那就是射频知识更新的没有那么快,不会说,你刚刚费九牛二虎之力把一个东西学会,就发现用不上了。
说回,麦克斯韦方程。时变麦克斯韦方程的差分形式,如下图所示。

上面的时变场分量,是空间坐标x,y,z和时间变量t的实函数。
麦克斯韦方程,对任何时间函数都是成立的,不过这任何函数的计算则是相当复杂的。
傅里叶变换可以将任何函数,转换成多个时谐函数的集合。所以,可以主要来看麦克斯韦方程的时谐解。
对于一个实正弦信号,可以用下列形式表示:
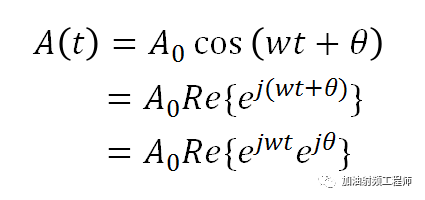
A(t)可以使用相量表示,即:
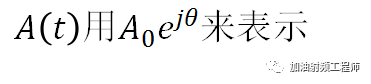
从上面公式可知,A(t)的相量形式,省去了Re{}以及e(jwt)。这样做的前提是:
(1) 被表示的变量是一个实数,所以不需要将Re{}写出来
(2) 处理的系统是线性时不变系统,即变量的频率分量是不变的,因此,不需要把e(jwt)写出来。
所以,用相量来表示一个正弦信号时,只要写出其幅度和相位就可以了。
不过,虽然不用写出来,但是需要记住的是,其实这两项是存在的。如果对A(t)进行求导的话,不能忘记还有时间的存在,即:
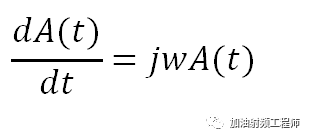
因此,麦克斯韦的相量形式如下图所示。
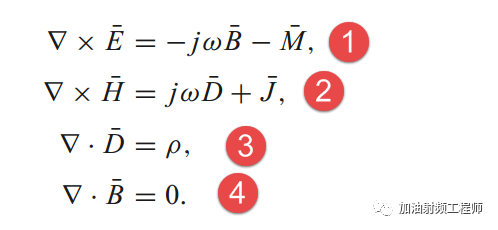
在自由空间中,电场与电通量密度,磁场与磁通量密度之间有下列的简单的关系式,称为本构关系。

以上,都是假设电场和磁场都存在于自由空间里,但是在实际过程中,媒质是经常性存在的,就像开头所说的板材。
虽然媒质的存在,让计算变得复杂,但是因为这些材料的存在,才出现了射频微波的蓬勃发展。
在自由空间中,场分量是通过本构关系,互相关联起来的。在媒质中,同样如此。
对于介电材料,施加在上面的电场,会导致材料内的原子或分子发生极化,从而产生电偶极矩,改变总的电通量。

那物质是线性的,是个啥意思?
实验发现,如果施加的电场不是太大的话,极化的程度与电场呈线性关系。所以,如果一个材料,其极化和电场之间满足线性关系,则称之为线性电介质。
在一个电导率为σ的材料中,导体电流密度为:
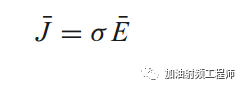
因此麦克斯韦方程中磁场的旋度方程,可以表示为

从上面可以看到,介电阻尼引起的损耗与电导率损耗无法区分。
因此,可以将:
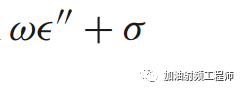
看成总的有效导电率。
并定义损耗角正切为:
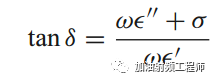
即虚部和实部的比值。
复介电常数的虚部,表示的是损耗,分别来自由介电阻引起的损耗和电导率产生的损耗。在自由空间内,复介电常数的虚部为0,只有实部,因此是无耗的。
一般的PCB板材,都是绝缘材料,所以 电导率σ为0,此时损耗角正切为:
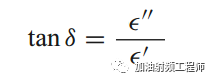
而相对介电常数是复介电常数的实部与自由空间中介电常数的比值。
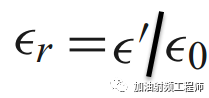
所以说,板材为啥用介电常数和损耗角正切来表征呢?
这是因为相对介电常数和损耗角正切确定了,那么复介电常数就确定了,然后电通量和电场之间的关系也就有了。
等等,你怎么光考虑电场,不考虑磁场啊?
材料的介电常数 (permittivity)有了,那磁导率 (permeability)呢?
其实类似的,磁介质中发生的现象和电介质中类似。
施加在介质中的磁场,会在磁介质中产生磁偶极矩,从而产生磁极化。
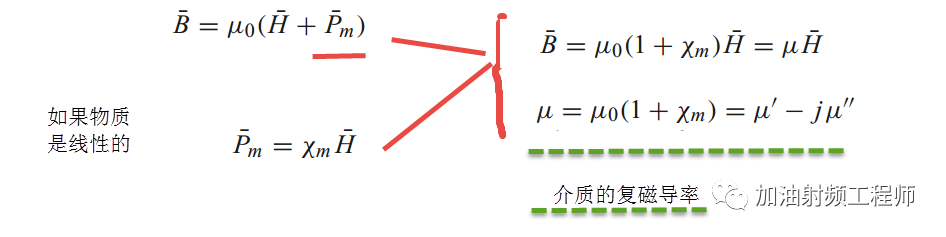
同样的,复磁导率的虚部,也表示损耗。
相对磁导率定义为:
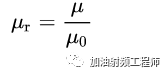
那可能大家就会觉得奇怪了,既然也有相对磁导率,那为啥在PCB板材的手册中,没有看到呢?
这是因为,大多数非磁性材料,其相对磁导率都为1,而此损耗角正切为0.比如说在HFSS里面的Rogers4350的材料参数。
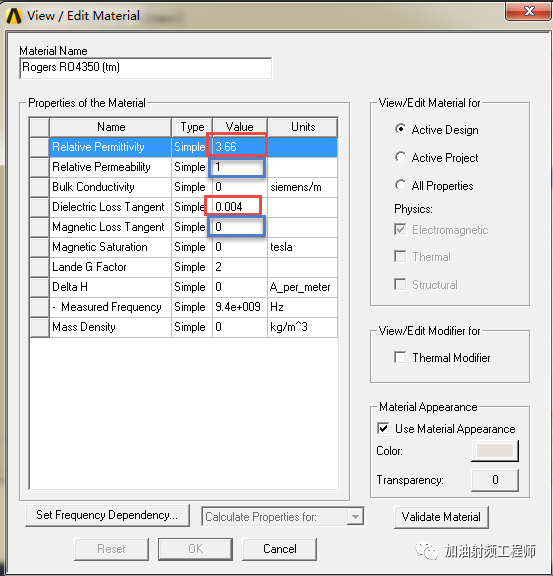
知道了复数介电常数和复数磁导率后,麦克斯韦在媒质中的相量形式,如下图所示。
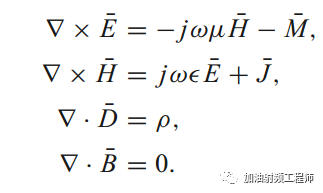
本构关系等式,如下图所示:
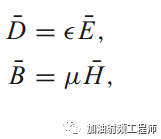
而复数介电常数,可以由相对介电常数和损耗角正切来表示;复数磁导率,对于非磁性材料来讲,相对磁导率为1,磁损耗角正切为0.
所以,板材可以用相对介电常数和损耗角正切来表征其射频上的性能。
审核编辑:刘清
-
PCB的介质损耗角是什么“∠”?2025-04-21 368
-
介电常数只需要测试容值?介电常数与介电损耗有什么区别#同惠电子 #介电常数 #介电损耗安泰小课堂 2024-07-09
-
PCB板厂家的板材(FR4)厚度及介电常数2015-05-04 19306
-
高频PCB基材介电常数与介电损耗的特性与改性进展2012-04-11 1798
-
介电常数怎么测试_介电常数测试方法2017-12-05 74490
-
电介质介电常数大好还是小好_介电常数越大代表什么2018-03-07 318390
-
PCB线路板材料的特性表征详细说明2020-10-22 1477
-
介质损耗角正切值的测量方法2021-09-26 9080
-
关于高频绝缘材料介电常数介质损耗测试系统的介绍2021-04-26 2990
-
介电常数检测仪的特点和用途2022-10-17 1239
-
介电常数用什么仪器测量?2023-03-24 2429
-
相对介电常数和介电常数的关系2024-01-14 19489
-
材料电磁学特征表征2024-11-11 1672
-
相对介电常数与介质损耗的关系2025-01-10 3625
-
用HD6000异频介质损耗测试仪测量介质损耗角方法2025-04-02 876
全部0条评论

快来发表一下你的评论吧 !

