3D曲面重建之移动最小二乘法

本文我们思考这样一个问题：如何在一组逐点值的给定域上估计该域的一般函数？这种估计对于给定域上PDE数值的求解，根据扫描数据进行表面重建，或者理解采集到数据的数据结构都有所帮助。下面介绍几种常见的最小二乘法：

一、全局最小二乘估计

 

 

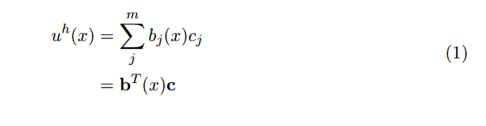
为了解决多项式拟合中的未知系数，我们构建如下的目标函数：

 

 

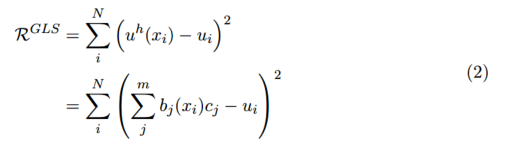
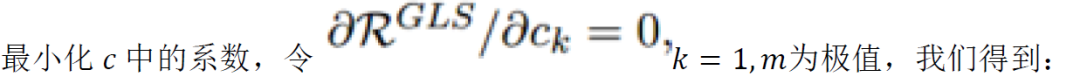
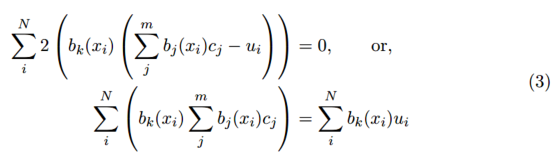
然后我们可以写个归一化方程为：

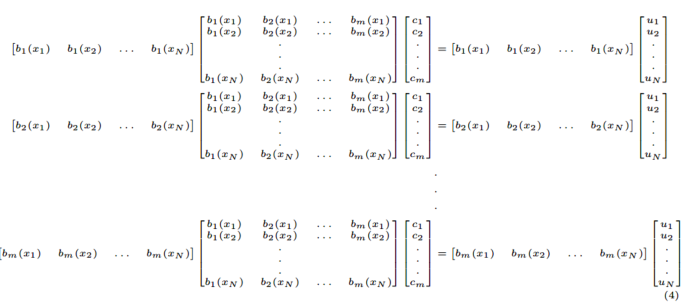
用矩阵的形式表示为：

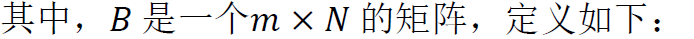
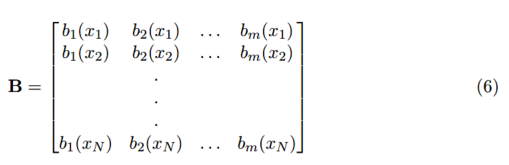
这个矩阵方程也可以直接用于计算系数向量  ：或者在大型系统中使用迭代的方法。

 

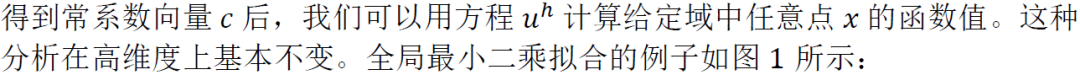
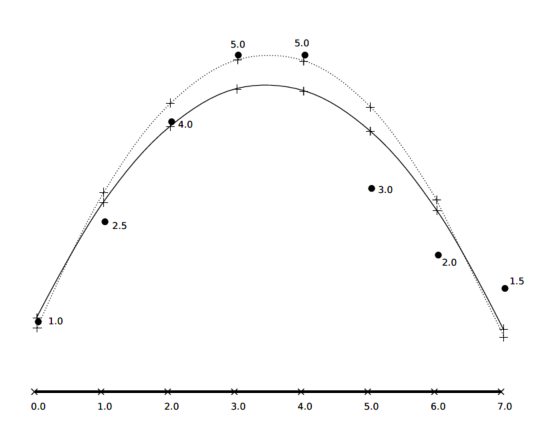
图1 全局最小二乘（实曲线）

二、全局加权最小二乘拟合

我们可以为每个数据值分配一个权重用于最小二乘拟合中，这样我们将目标函数最小化为：

 

 

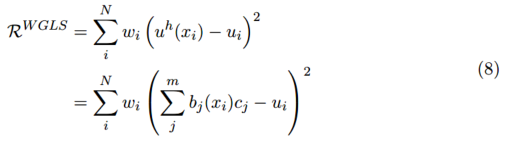
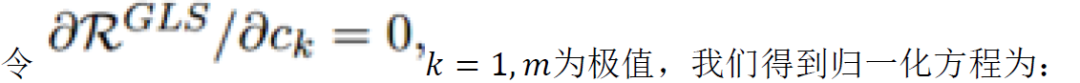
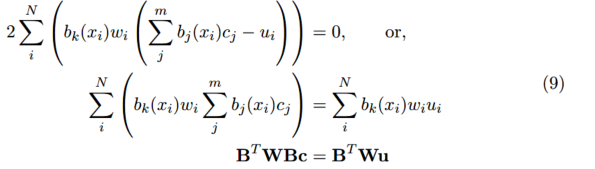
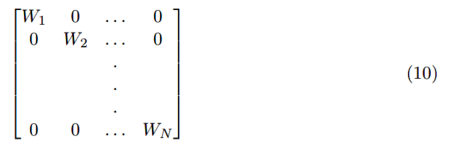
归一化方程的解为：

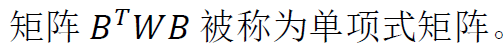
三、加权局部最小二乘

在全局最小二乘拟合中，我们假设整个域中都可以用一个单一的多项式精确地描述数据所代表的函数。但是，对于大型、复杂的数据集，这将要求我们拟合出一个不理想的高阶多项式，即便如此，这也不能捕获数据的所有特征。所以，为了替代全局解决方案，我们尝试通过对每个数据点 及其邻域拟合出一个低阶多项式来获得更好的解决方案。因此，有 个最小二乘拟合的值 ，每个值都是点 的近似值并且每个点的系数向量  都不同。注意：不同于其它讨论的方法，这不是一种公认的方法并且也不常见。它仅仅是为了我们更好的理解下一部分将要介绍的移动最小二乘法。 

 

 

 

 

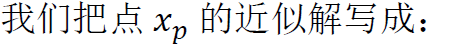
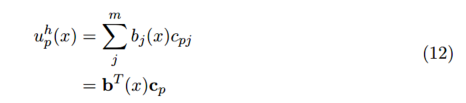
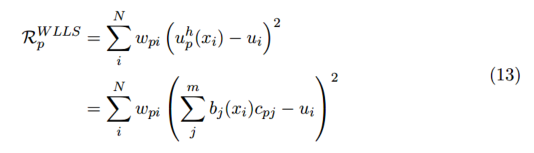
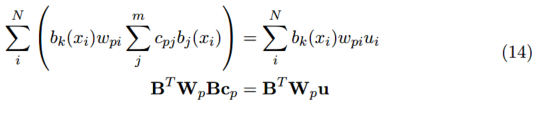
用通用的方法就可解决。

 

 

 

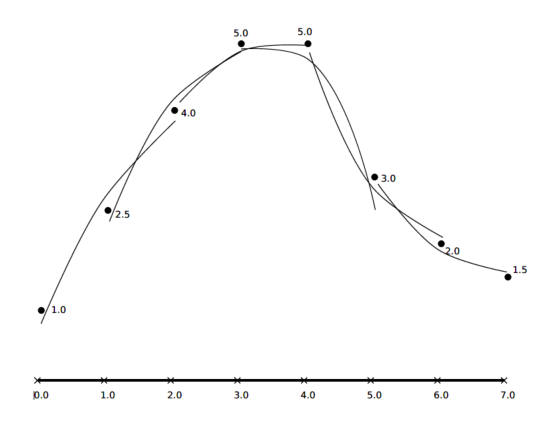
图2 加权局部最小二乘拟合

四、移动最小二乘法

 

 

 

 

 

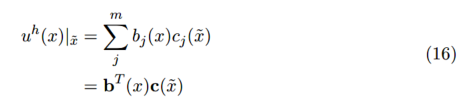
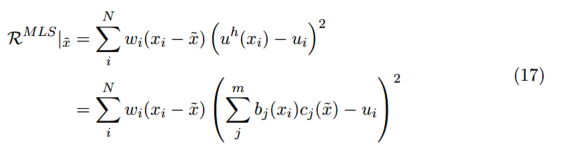
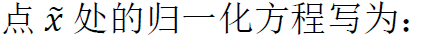
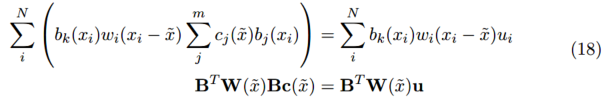
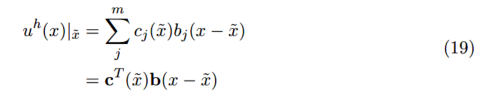
总结