将Paxos和Raft统一为一个协议：Abstract-paxos

前言

前言

之前写了一篇 Paxos 的直观解释，用简单的语言描述了 paxos 的工作原理，看过的朋友说是看过的最易懂的 paxos 介绍，同时也问我是否也写一篇 raft 的。但 raft 介绍文章已经很多很优质了，感觉没什么可写的，就一直拖着。

后来想起来，在分布式岗的面试中，会经常被问到 raft 和 paxos 有什么区别， 虽然可能会惹恼面试官，但我会说：没区别。今天介绍一个把 paxos 和 raft 等统一到一起的分布式一致性算法 abstract-paxos，解释各种分布式一致性算法从 0 到 1 的推导过程。算是填了 raft 的坑，同时在更抽象的视角看 raft，也可以很容易看出它设计上的不足和几个优化的方法。

为了清楚的展现分布式一致性协议要解决的问题，我们将从 0 开始，即从 2 个基本需求：技术爆炸和猜疑链 信息确定 和 分布式 开始。推导出所有的分布式强一致协议的统一形式，然后再把它特例化为 raft 或 paxos。

本文的整个推导过程顺着以下过程，从 assumption 开始，最终达到 protocol：

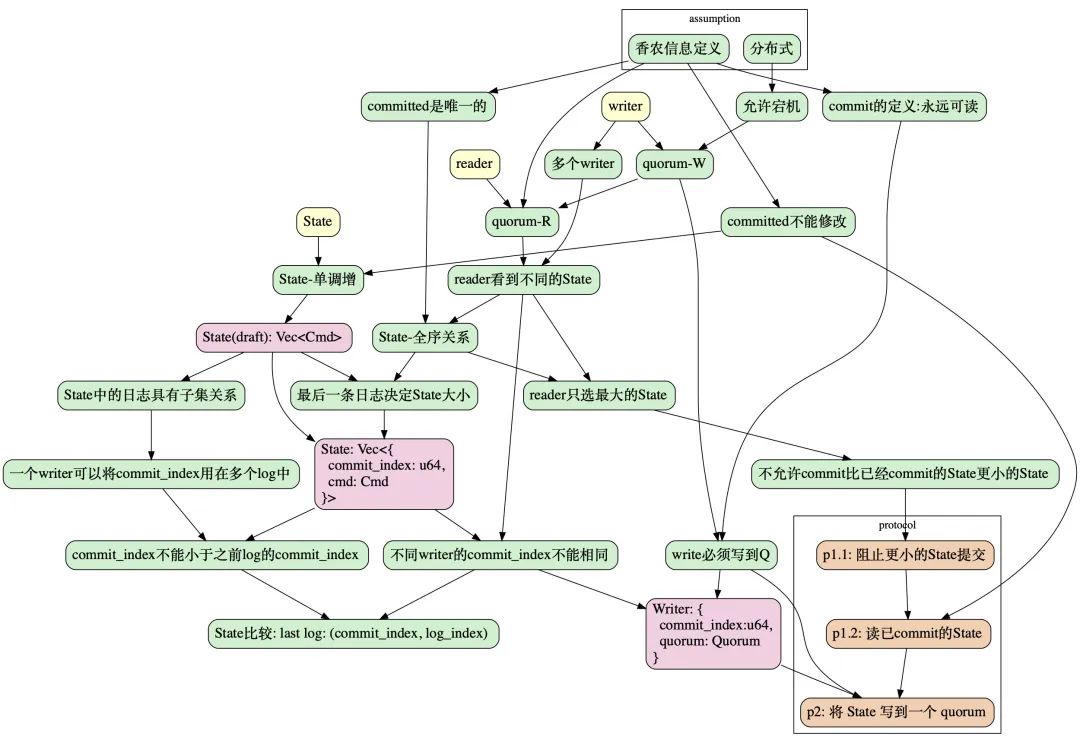
本文结构

本文结构

提出问题

协议推导

定义 commit

定义 系统状态（State）

协议描述

工程实践

成员变更

使用 abstract-paxos 描述 paxos

使用 abstract-paxos 描述 raft

问题

问题

从我们要解决的问题出发：实现一个分布式的、强一致的存储系统。存储系统是存储信息的，我们首先给出信息和分布式存储的定义：

香农信息定义

香农信息理论定义： 信息是用来消除随机不定性的东西 。

具体来说，对某个信息的读操作，每次得到的内容应该都是唯一的，确定的。这个定义将贯穿本文，作为我们设计一致性协议的最根本的公理。

分布式存储

存储系统可以看做一个可以根据外部命令（Cmd）改变系统状态（State）的东西。例如一个 key-value 存储，set x=1 或 set x=y+1 都可以看做一个 Cmd。

而分布式则表示存储系统由多个节点（node）组成（一个 node 可以简单的认为是一个进程），存储系统的操作者是多个并发的写入者（write）和读取者（reader）。

而一个可靠的分布式也意味着它必须允许宕机：它必须能容忍部分节点宕机还能正常工作。

所以它必须有 冗余 ，即：每个节点存储一个 State 的副本，而我们需要的分布式一致性协议的目的，就是保证对外界观察者（reader）能够提供保证香农信息定义的 State 的信息。

系统要提供在 writer 或 reader 只能访问到部分节点时系统也能工作，这里的部分节点在分布式领域一般定义为一个 quorum ：

Quorum

Quorum

一个 quorum 定义为一个节点（node）集合。e.g. HashSet。

在这个系统中，分布式的特性要求 writer 只需能联系到一个 quorum 就可以完成一个信息的写入，即：实现 quorum-write。 而 reader 只需要联系到一个 quorum 就可以确定的读取到 信息 ，即实现 quorum-read 。

因为 writer 写入的信息 reader 必须能读到，所以任意 2 个 quorum 必须有交集：

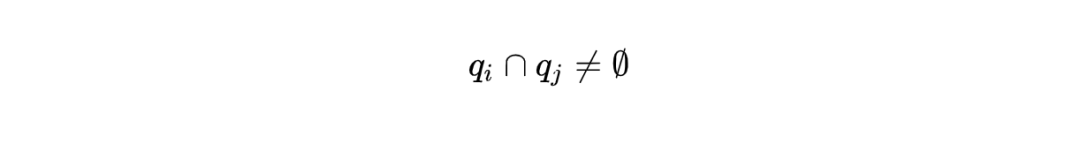
大部分时候， 一个 quorum 都是指 majority，也就是多于半数个 node 的集合。例如【a,b】，【b,c】，【c,a】是集合【a,b,c】的 3 个 quorum。

如果 任何一个 reader 都能通过访问一个 quorum 来读到某个数据，那么这条数据就满足了 香农信息定义 ，我们称这条数据为 commit 的。

Commit

Commit

根据 香农信息定义 ， 如果写入的数据一定能通过某种方法读取到，则认为它是 committed 。

如果某个数据有时能读到有时不能，它就不是一个 信息 。

不确定读的例子

例子1: 读到不确定的结果

例如下面 3 个 node N1，N2，N3 的 例子1，

N1 存储了[x,y]，

N3 存储了 [z]，

使用 quorum-read 去读的时候，有时能得到【x,y】（访问 N1,N2），有时能得到【z】（访问 N2,N3）

所以【x,y】和【z】在这个系统中都不是信息，都不是 commit 完成的状态。

例子2: 总能读到的结果

而像以下这个 例子2， 一次 quorum-read 不论落到哪 2 个 node 上，都能看到【z】

所以【z】在这个系统中有机会成为一个信息。

这时还不能确定【z】是一个信息，因为这里如果 reader 访问 N1,N2，还涉及到是选 【x,y】还是选 【z】作为系统当前的状态的问题，也就是说读取的结果还不能保证唯一。后面继续讨论。

因此，我们就得到了在一个多副本的存储系统中 commit 完成的条件：

commit-写 quorum ：以保证任何 reader 都可读到。

commit-唯一 ：以保证多个 reader 返回相同的结果。

commit 后不能修改 ：以保证多次读返回同样的结果。

我们先解释这几个条件，接着讨论如何设计一个 commit 的协议来满足这几个条件，从而达到一致性。

commit-写 quorum

一个数据必须有机会被 reader 见到：即一个数据已经写到一个 quorum 中： commit-写 quorum 。

commit-唯一

这里唯一是指，在可见的基础上，增加一个唯一确定的要求：

例如在上面的例子2 中，如果 reader 一次读操作访问到 N1, N2 这 2 个 node，那么它收到的看到的 2 个 State 的副本分别是【x,y】和【z】，这 2 个 State 的副本都是可见的，但作为一个存储系统，任何一个 reader 都必须选择同样的 State 作为当前系统的 State（否则违反香农信息定义的消除不确定性的原则）。

所以我们对读操作还要求 reader 能有办法在所有可见的副本中唯一确定的选择一个 State，作为读操作的结果。

commit 后不能修改

香农信息定义要求一个 commit 完成的 State 必须永远可被读到：即要求 commit 的 State 不能被覆盖和修改，只能 增加 。

State 不能被修改有点反直觉,，因为一般的存储系统,，先存储了 x=1，还可以修改为 x=2。看起来是允许修改的。

这里可以这样理解：

经历了 x=1，再到 x=2 的一个 State （【x=1, x=2】），跟直接到 x=2 的 State（【x=1,】）是不同的。这个不同之处体现在：可能有个时间点，可以从第一个 State 读出 x=1 的信息，而第二个 State 不行。

常见的 State 定义是：一个 Cmd 为元素的，只允许 append 的 list：Vec.

这也就是一个记录变更操作（Cmd）的日志（log），或称为 write-ahead-log(WAL). 而系统的 State 也由 WAL 唯一定义的。在一个典型的 WAL + State Machine 的系统中（例如 leveldb），WAL 决定了系统状态（State），如这 3 条log：【set x=1, set x=2, set y=3】，而平常人们口中的 State Machine，仅仅是负责最终将整个系统的状态呈现为一个 application 方便使用的形式，即一般的 HashMap 的形式：【x=2, y=3】。

所以在本文中，WAL 是真实的 State，我们这里说的不能修改，只能追加，就是指 WAL 不能修改，只能追加。本文中我们不讨论 State Machine 的实现。

如果把存储系统的 State 看做是一个集合，那么它必须是一个只增的集合：

State

State

本文的目的仅仅是来统一 paxos 和 raft，不需要太复杂，只需把 State 定义为一个只能追加的操作日志：

log 中的每个 entry 是一个改变系统状态的命令（Cmd）。

这是 State 的初步设计，为了实现这个一致性协议，后面我们将对 State 增加更多的信息来满足我们的要求。

根据 commit-写 quorum 的要求，最终 State 会写到一个 quorum 中以完成 commit，我们将这个过程暂时称作 phase-2 。它是最后一步，在执行这一步之前，我们需要设计一个协议，让整个 commit 的过程也遵守：

commit-唯一，

commit 后不能修改

的约束。

首先看如何让 commit 后的数据 唯一， 这涉及到 reader 如何从 quorum 中多个 node 返回的不同的 State 副本中选择一个作为读操作的最终结果：

reader：找出没有完成 commit 的 State 副本

reader：找出没有完成 commit 的 State 副本

根据 香农信息定义 ， 已经 commit 的 State 要求一定能被读到，但多个 writer 可能会（在互不知晓的情况下）并发的向多个 node 写入不同的 State。

写入了不同的 State 指：两个 State：s₁, s₂，如果 s₁ ⊆ s₂ 和 s₂ ⊆ s₁ 都不满足，那么只有一个是可能被 commit 的。否则就产生了信息的丢失。

而当 reader 在不同的 node 上读到 2 个不同的 State 时，reader 必须能排除其中一个肯定没有 commit 的 State，如 例子2 中描述问题。

即，commit-唯一要求：两个非包含关系的 State 最多只有一个是可能 commit 状态的。并要求 2 个 State 可以通过互相对比，来排除掉其中一个肯定不是 commit 的 State，这表示 State 之间存在一个 全序关系 ：即任意 2 个 State 是可以比较大小的，在这个大小关系中：

较大的是可能 commit 的 ，

较小的一定不是 commit 的 。

State 的全序关系

State 的全序关系

State 的全序关系来表示 commit 的有效性，但到目前为止，State 本身是一个操作日志，也就是一个 list，list 之间只有一个 偏序关系 ，即包含关系。互不包含的 2 个 list 无法确定大小关系。

例如, 如果在 2 个节点上分别读到 2 个 log：【x, y, z】和【x, y, w]】，无法确认哪个是可能 commit 的，哪个是一定没有 commit 的：

所以 State 必须具备更多的信息让它能形成全序关系。

并且这个全序关系是可控的：即， 对任意一个 State，可以使它变得比任何已知 State 大。 否则，writer 在试图 commit 新的数据到系统里时将无法产生一个足够大的 State 让 reader 去选它，导致 writer 无法完成 commit。

给 State 添加用于排序的信息

例如下面 例子3 中，如果每个 node 都为其 State 增加一个序号（在例子中的角标位置），那么 reader 不论联系到哪 2 个节点，都可以确定选择序号更大的【y】作为读取结果，这时就可以认为【y】是一个信息了。

而 commit 后不能修改 的原则要求系统所有的修改，都要基于已 commit 的 State，所以当系统中再次 commit 一个数据后可能是在【y】s 之上追加【z,w】：

为了实现上述逻辑， 一个简单的实现是让最后一个 log 节点决定 2 个 State 之间的大小关系。

于是我们可以对 State 的每个 log 节点都需要加入一个偏序关系的属性 commit_index（本文为了简化描述, 使用一个整数）来确定 State 的全序关系：

在后面的例子中，我们将 commit_index 写成每条 log 的下标的形式，例如

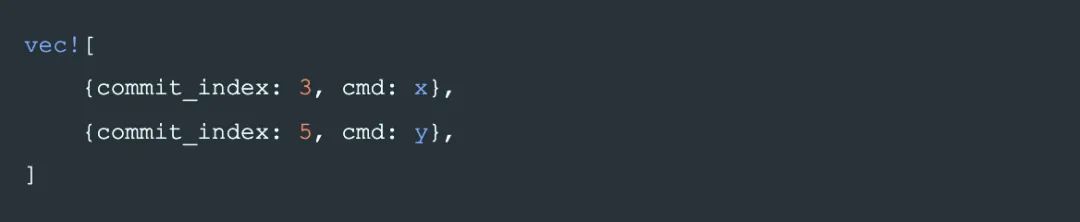
将表示为：

同时定义一个 method 用来取得一个 State 用于比较大小的 commit_index：

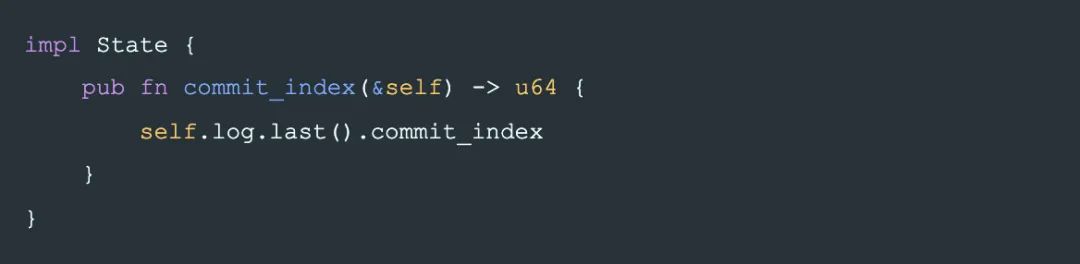
commit_index 的值是由 writer 写入 State 时决定。即 writer 决定它写入的 State 的大小。

如果两个 State 不是包含关系，那么大小关系由 commit_index 决定。writer 通过 quorum-write 写入一个足够大的 State，就能保证一定被 reader 选择，就完成了 commit。

这也暗示了：

非包含关系的 2 个 State 的 commit_index 不能相同。否则 State 之间无法确定全序关系。即，任意 2 个 writer 不允许产生相同的 commit_index。

同一个 writer 产生的 State 一定是包含关系，不需要使用 commit_index 去决定大小：
对于 2 个包含关系的 State：sₐ ⊆ sᵦ，显然对于 reader 来说，应该选择更大的 sᵦ，无需 commit_index 来确定 State 的大小。因此一个 writer 产生的 State，允许多个 log 的 commit_index 相同。并用 log 的长度确定大小关系。

这样我们就得到了 State 的大小关系的定义：

State-全序定义

两个 State 的顺序关系：通过 commit_index 和 log 长度确定，即比较 2 个 State 的：（s.commit_index(), s.log.len()）。

上面提到，commit_index 是一个具有偏序关系的值，不同类型的 commit_index 会将 abstract-paxos 具体化为某种协议或协议族，例如：

如果 commit_index 是一个整数，那就是类似 paxos 的 rnd。

而 raft 中，与 commit_index 对应的概念是【term, Option】，它是一个偏序关系的值，也是它造成了 raft 中选举容易出现冲突。

关于 abstract-paxos 如何映射为 paxos 或 raft，在本文的最后讨论。

另一方面，从 writer 的角度来说：

如果一个 writer 可以生成一个 commit_index 使之大于任何一个已知的 commit_index，那么这时 abstract-paxos 就是一个活锁的系统：它永远不会阻塞，但有可能永远都不会成功提交。例如 paxos 或 raft

如果一个 writer 无法生成任意大的 commit_index，那么它就是一个死锁的系统，例如 2pc

当然也可以构造 commit_index 使 abstract-paxos 既活锁又死锁，那么可以认为它是一个结合了 paxos 和 2pc 的协议。

有了 State 之间的全序关系，然后再让 writer 保证 phase-2 写到 quorum 里的 State 一定是最大的，进而让 reader 读取时都可以选择这个 State，达到香农信息定义要求的信息确定性要求，即 commit-唯一的要求，完成 commit：

下面来设计协议，完成这一保证：

协议设计

协议设计

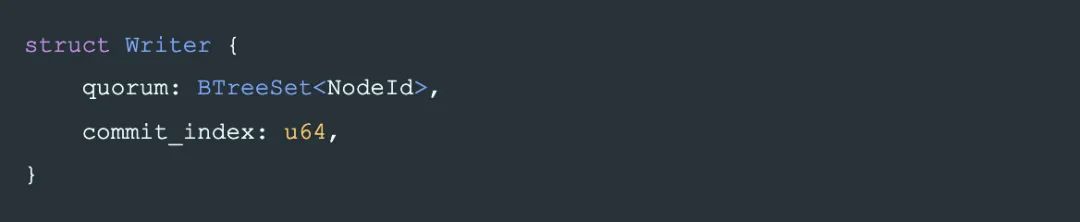
现在我们来设计整个协议，首先，有一个 writer w，w 最终 commit 的操作是在 phase-2 将 State 写到一个quorum。writer 的数据结构定义为一个它选择的 quorum，以及它决定使用的 commit_index：

因为 reader 读取时，只选它看到的最大的 State 而忽略较小的。所以如果一个较大的 State 已经 commit，那么整个系统就不能再允许 commit 一个较小的 State，否则会造成较小的 State 认为自己 commit 完成，但永远不会被读到，这就造成了信息丢失。

例如下面 例子5 中描述的场景，如果最终写入 State 前不做防御，那么是无法完成 commit 的：假设有 2 个 writer w₁, w₂ 同时在写它们自己的 State 到自己的 quorum：

t1 时间 w₁ 将 【y₅】写到 N2, N3,

t2 时间 w₂ 将 【x₁,y₇】写到了 N1。

那么当一个 reader 联系到 N1, N2 进行读操作时，它会认为【x₁,y₇】是 commit 完成的， 而真正由 w₁ commit 的数据就丢失了，违背了 香农信息定义 。

所以： writer 在 commit 一个 State 前，必须阻止更小的 State 被 commit 。这就是 phase-1 要做的第一件事：

Phase-1.1 阻止更小的 State 被 commit

假设 writer w₁ 要写入的 State 是 s₁，在 w₁ 将 s₁ 写到一个 quorum 前，整个系统必须阻止小于 s₁ 的 State 被 commit。

因为不同的 writer 不会产生同样的 commit_index。所以整个系统只需阻止更小的 commit_index 的 State 被 commit：

为达到这个目的，在这一步，首先通知 w₁ quorum 中的每个节点：拒绝所有其他 commit_index 小于 w₁。commit_index 的 phase-2 请求。

于是我们基本上可以确定 node 的数据结构，它需要存储 phase-2 中真正写入的 State，以及 phase-1.1 中要拒绝的 commit_index：

在后面的例子中，我们将用一个数字前缀表示 node 中的 commit_index，例如：

将表示为:

一个直接的推论是, 一个 node 如果记录了一个 commit_index , 就不能接受更小的 commit_index , 否则意味着它的防御失效了: Node.commit_index 单调增。

如果 writer 的 phase-1.1 请求没有被 quorum 中全部成员认可，那么它无法安全的进行 phase-2， 这时只能终止。

最后我们整理下 phase-1.1 的流程：

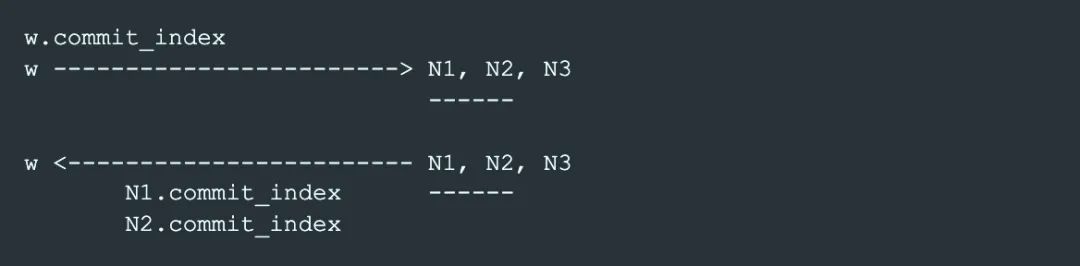
每个 node 在 P1Reply 中返回自己之前保存的 commit_index，writer 拿到 reply 后跟自己的commit_index 对比，如果 w.commit_index >= P1Reply.commit_index，表示 phase-1.1 成功。

完成 phase-1.1 后，可以保证没有更小的 State 可以被 commit 了。

然后，为了满足 commit 后不能修改 的原则，还要求 s₁ 必须包含所有已提交的，commit_index 小于 s₁.commit_index() 的所有 State：

Phase-1.2 读已完成 commit 的 State

因为 commit 的条件之一是将 State 写入一个 quorum，所以 w₁ 询问 w₁.quorum，就一定能看到小于 w₁.commit_index 的，已 commit 的其他 State。这时 writer 是一个 reader 的角色（如果遇到大于 w₁.commit_index 的 State，则当前 writer 是可能无法完成提交的，应终止）。

且读过某个 node 之后，就不允许这个 node 再接受来自其他 writer 的，小于 w₁.commit_index 的 phase-2 的写入。以避免读后又有新的 State 被 commit，这样就无法保证 w₁ 写入的 State 能包含所有已 commit 的 State。

w₁ 在不同的节点上会读到不同的 State，根据 State 的全序的定义，只有最大的 State 才可能是已 commit 的（也可能不是, 但更小的一定不是），所以 w₁ 只要选最大的 State 就能保证它包含了所有已 commit 的 State。

在最大 State 的基础上，增加 w₁ 自己要写的内容。最后进行 phase-2 完成 commit 。

phase-1.1 跟 phase-1.2 一般在实现上会合并成一个 RPC，即 phase-1。

Phase-1

Phase-1: Data

Phase-1: Req

Phase-1: Reply

Phase-1: Handler

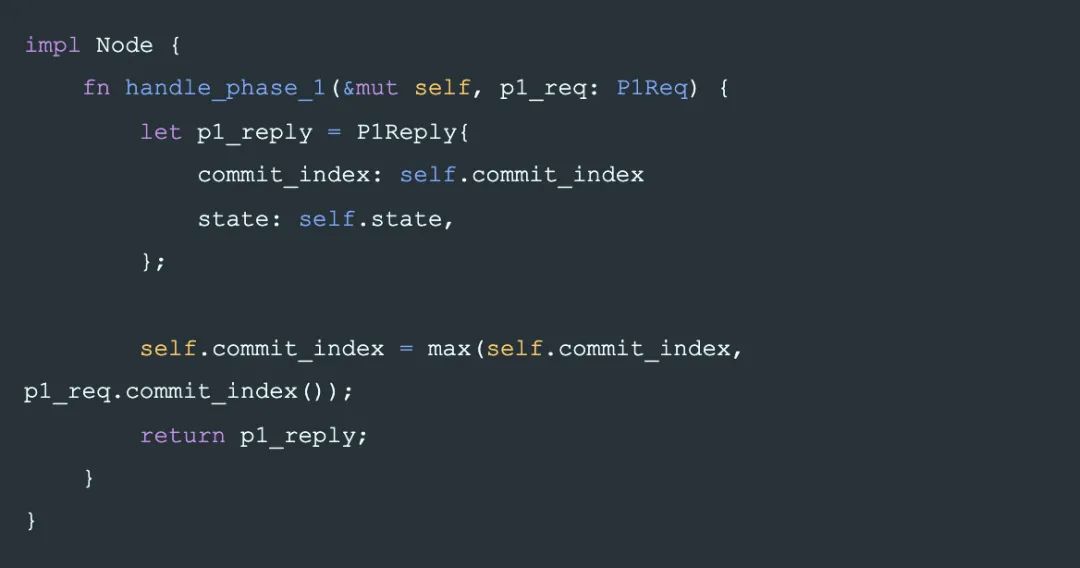
Phase-2

最后，保证了 s₁ 当前最大，和 commit 后不能修改这两个条件后，第 2 阶段，writer 就可以安全的写入一个 s₁ 完成 commit。

如果 phase-2 完成了，则表示 commit 一定成功了，任何一个 reader 都能读到唯一确定的 State s₁（除非有更大的 State 被写入了）。

反之，如果有其他 writer 通过 phase-1 阻止了 w₁.commit_index 的写入，那么 w₁ 的 phase-2 就可能失败，这时就退出 commit 过程并终止。

这里有一个学习分布式系统时经常提出的问题：

Q:

因为在 phase-1 中 w 已经阻止了所有小于 w.commit_index 的 State 的提交，phase-2 是否可以写入一个小于 w.commit_index 的 State？

A:

不可以，phase-2 写入的 State 的commit_index() 跟 w.commit_index 相等时才能保证安全，简单分析下：

显然要写的 s₁.commit_index() 不能大于 w₁.commit_index，因为 phase-1.1 没有保护大于 w₁.commit_index 的 State 的写入。

虽然在 phase-1 阶段，系统已经阻止了所有小于 s₁.commit_index() 的其他 State 的 phase-2 写入，如果 w₁ 写的 State 的 s_1.commit_index() 小于w.commit_index，那么系统中可能存在另一个稍大一点的 State (但没有 commit，导致 reader 不认为 s₁ 是 commit 的。

例如：

一个 writer w₅ 在 t1 时间完成了 phase-1，在 t2 时间 phase-2 只写入了 N1；

然后另一个 writer w₆ 在 t3 时间完成了 phase-1，phase-2 只写入了一个较小的 commit_index=4 的 State。

那么某个 reader 如果通过访问 N1,N2 读取数据，会认为 N1 上的【x₅】是 commit 的，破坏了 香农信息定义。

所以必须满足：s₁.commit_index() == w₁.commit_index

这时，只要将 State 写入到 w₁.quorum，就可以认为提交。

对应每个 node 的行为是：在每个收到 phase-2 请求的节点上，如果 node 上没有记录拒绝 commit_index 以下的 phase-2 请求，就可以接受这笔写入。

一个推论：一个节点如果接受了 commit_index 的写入，那么同时它应该拒绝小于 commit_index 的写入了。因为较小的 State 一定不是 commit 的，如果接受，会造成信息丢失。

Phase-2: data

和 phase-1 类似，一个 node 返回它自己的 commit_index 来表示它是否接受了 writer 的 phase-2 请求。

在 P2Req 中，如果 state 是完整的，commit_index 总是与 state.commit_index() 一样，可以去掉；这里保留是因为之后将会讨论到的分段传输：每个请求只传输 State 的一部分，这时就需要额外的 P2Req.commit_index。

Phase-2: Req

Phase-2: Reply

Phase-2: Handler

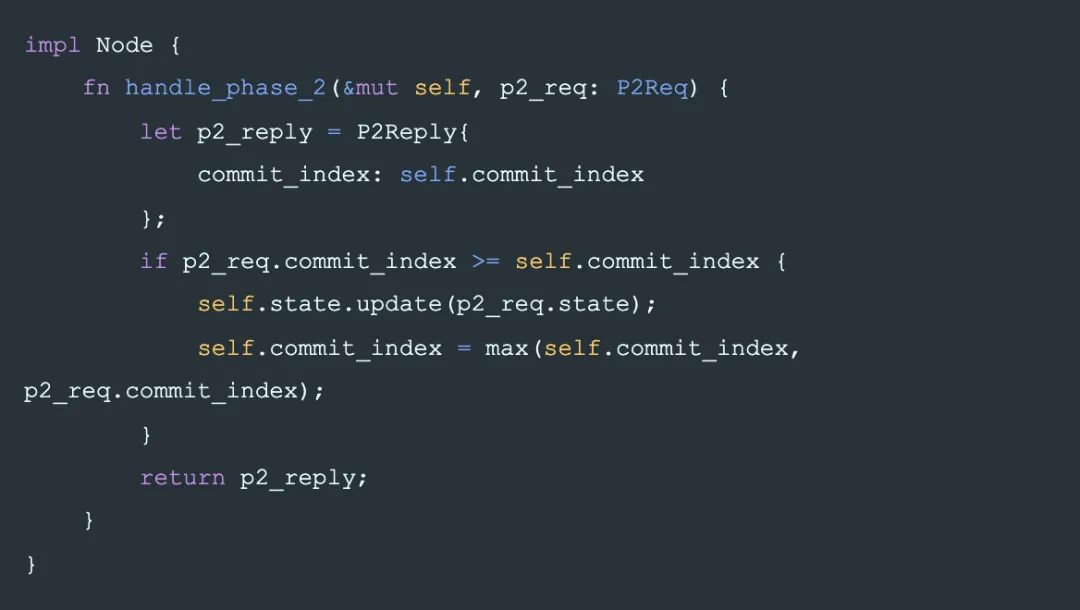
也就是说 phase-2 不止可能修改 Node.state，同时也会修改 Node.commit_index。

这里也是一个学习分布式容易产生误解的地方，例如很多人曾经以为的一个 paxos 的bug: paxos-bug。

这里也很容易看出为何在 raft 中必须当前 term 复制到 quorum 才认为是 commit 了。

可重复的 phase-2

要保证写入的数据是 commit 的，只需保证写入一个 quorum 的 State 是最大的即可。所以 writer 可以不断追加新的日志，不停的重复 phase-2 。

Writer 协议描述

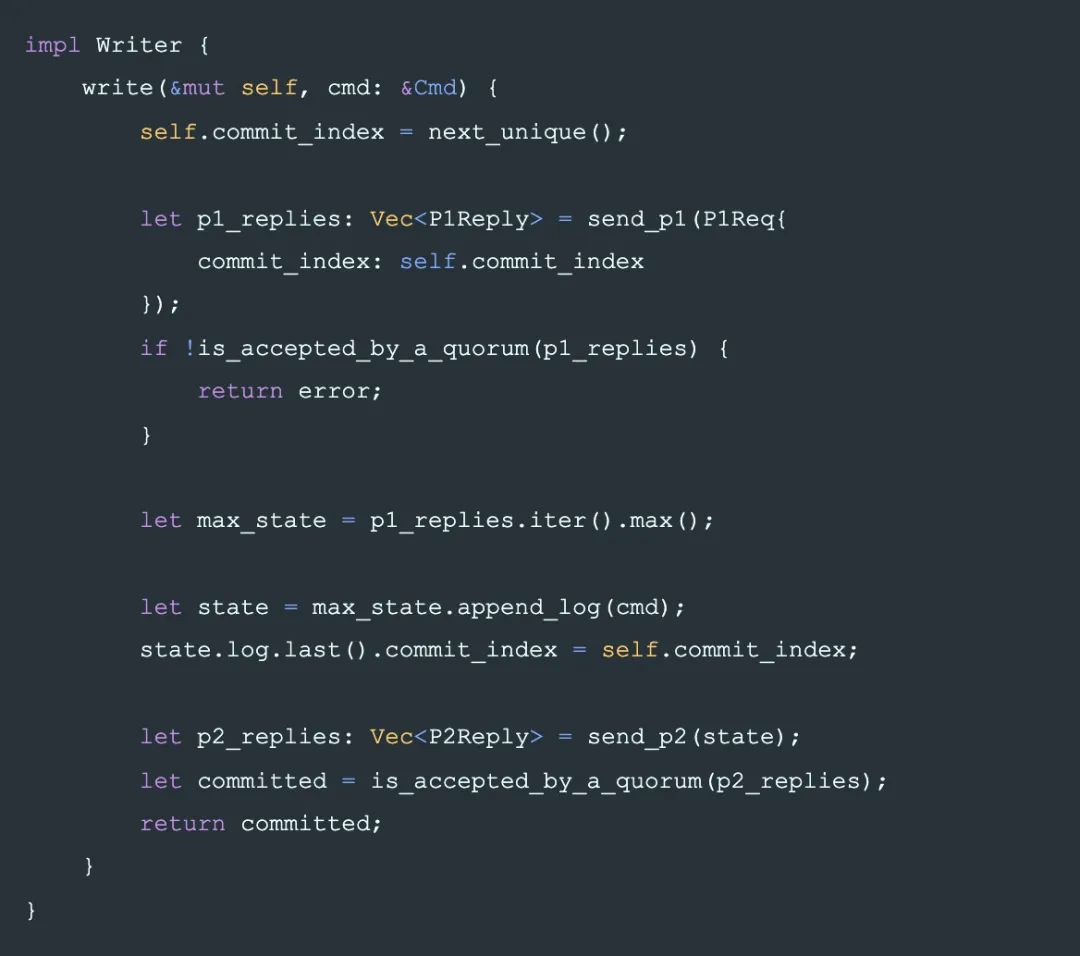
Writer 协议描述

最后将整个协议组装起来的是 writer 的逻辑，如前所讲，它需要先在一个 quorum 上完成 phase-1 来阻止更小的 State 被 commit，然后在 quorum 上完成 phase-2 完成一条日志的提交。

工程实现

工程实现

Phase-2: 增量复制

这个算法的正确性 还需考虑工程上的方便，

到目前为止，算法中对 State 的写都假设是原子的。但在工程实现上， State 是一个很大的数据结构，很多条 log

所以在 phase-2 传输 State 的过程中，我们还需要一个正确的分段写的机制：

原则还是保证 香农信息定义 ，即：commit 的数据不丢失。

State 不能留空洞：有空洞的 State 跟没空洞的 State 不同，不能通过最后一条日志来确定其所在的 State 大小。

writer 在 phase-1 完成后可以保证一定包含所有已经 commit 的 State。

所以在一个接受 phase-2 的 node 上，它 Node.state 中任何跟 Writer.State 不同的部分都可以删除，因为不一致的部分一定没有被 commit。

以下是 phase-2 过程中删除 N3 上不一致数据的过程：

t1 时刻，writer W 联系到 N1，N2 完成 phase-1，读到最大的State【x₃,z₅】，添加自己的日志到最大 State 上：【x₃,z₅,w₆】，这时系统中没有任何一个 node 的 State 是 commit 完成状态的，一个 reader 可能选择【x₃,z₅】作为读取结果（访问N1,N2），可能选择【x₃,y₄】作为读取结果（访问N2,N3）。

但这时一个 State 的子集：【x₃】是commit完成的状态。

t2 时刻，W 向 N3 复制了一段 State：【x₃】，它是 N3 本地日志的子集，不做变化。
这时 reader 还是可能读到不同的结果，同样【x₃】是 commit 完成的状态。

t3 时刻，W 向 N3 复制了另一段 State z₅，它跟 N3 本地 State 冲突，于是 N3 放弃本地的一段与 writer 不一致的 Statey₄，将本地 State 更新为：【x₅,z₅】

这时【x₅,z₅】是 commit 完成状态。

t4 时刻，W继续复制 w_6 到 N3，这是【x₅,z₅,w_4】是 commit 完成状态。

Snapshot 复制

snapshot 复制跟 State 分段复制没有本质区别，将 State 中的 log 从 0 到某一范围以压缩后的形式传输的到其他 node。

成员变更

成员变更

为支持成员变更，我们先加入下面这几个行为来支持成员变更操作：

State 中某些日志（config日志）表示集群中的成员配置。

State 中最后一个成员配置（config）日志出现就开始生效。

config 日志与普通的日志写入没有区别。

config 定义一个集群的 node 有哪些，以及定义了哪些 node 集合是一个 quorum。

例如一个普通的3成员集群的 config 【{a,b,c}】，它定义的 quorum 有

再如一个由 2 个配置组成的 joint config【{a,b,c}, {x,y,z}】。它定义的 quorum 集合是【a,b,c】的 quorum 集合跟【x,y,】的 guorum 集合的笛卡尔积：

然后，我们对成员变更增加约束，让成员变更的过程同样保证香农信息定的要求：

成员变更约束-1

首先，显然有 2 个相邻 config 的 quorum 必须有交集 。否则新配置启用后就立即会产生脑裂。即：

在后面的讨论中我们将满足以上约束的 2 个 config 的关系表示为： cᵢ ~ cᵢ₊₁ 。

例如：假设 State 中某条日志定义了一个 joint config：【{a,b,c}, {x,y,z}】那么，

下一个合法的 config 可以是：

uniform config【{a,b,c}】，

或另一个 joint config 【{x,y,z}, {o,p,q}】。

但不能是【{a,x,p}】，因为它的一个 quorum【a,x}】与 上一个 config 的 quorum【{b,c}, {y,z}】没有交集。

成员变更Lemma-1

对 2 个 config cᵢ ~ cⱼ，以及 2 个 State Sᵢ 和 Sⱼ 如果 Sᵢ 和 Sⱼ 互相不是子集关系，Sᵢ 在 cᵢ 上 commit 跟 Sⱼ 在 cⱼ 上 commit 不能同时发生。

成员变更约束-2

因为 2 个不同 writer 提出（propose）的 config 不一定 有交集，所以为了满足 commit-唯一 的条件，包含新 config 的日志要提交到一个新，旧配置的 joint config 上。即, cᵢ₊₁ 必须在【cᵢ, cᵢ₊₁】上 commit. cᵢ₊₁ 之后的 State， 只需使用 cᵢ₊₁ 进行 commit。

但是，当 writer 中断，另一个 writer 看到 cᵢ₊₁ 时，它不知道 cᵢ₊₁ 处于变更中间，也就是说新的 writer 不知道现在的 commit 应该使用【cᵢ, cᵢ₊₁】，它只使用【cᵢ₊₁】。

所以对 config 日志向 joint config 的 commit 分为两步：

先在旧配置上拒绝更小的 State 的提交，再 propose 新配置。根据成员变更Lemma-1，即：至少将一个与 w.commit_index 相同的 State commit 到 cᵢ 上。

再 propose cᵢ₊₁，从日志 cᵢ₊₁ 之后的日志开始，都只需 commit 到 cᵢ₊₁ 上。

最后总结：

成员变更的约束条件

上一个 config 在当前 commit_index 上提交后才允许 propose 下一个配置。

下一个配置必须跟最后一个已提交的配置有交集。

成员变更举例

raft 只支持以下的成员变更方式

c1 → c1c2 → c2 → c2c3 → c3 …

其中 c1c2 指 c1 跟 c2 的 joint config，例如：

cᵢ ：【a, b, c】；

cᵢcⱼ：【{a, b, c}，{x, y, z}】。

abstract-paxos 可以支持更灵活的变更:

c1 → c1c2c3 → c3c4 → c4

或回退到上一个 config：

c1c2c3 → c1

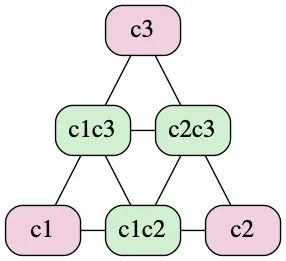
合法变更状态转换图示

下面的图示中简单列出了至多 2 个配置的 joint config 跟 uniform config 之间可转换的关系：

Variants

Variants

以上为 abastract-paxos 的算法描述部分。接下来我们将看它是如何通过增加一些限制条件，absract-paxos 将其变成 classic-paxos 或 raft 的。

秒变 Paxos

限制 State 中的日志只能有一条，那么它就变成 paxos。

不支持成员变更。

其中概念对应关系为：

abstract-paxos	classic-paxos
writer	proposer
node	acceptor
Writer.commit_index	rnd/ballot
State.commit_index()	vrnd/vbal

秒变 Raft

Raft 为了简化实现（而不是证明），有一些刻意的阉割：

commit_index 在 raft 里是 一个 偏序关系 的 tuple，包括：

term

和是否投票给了某个 Candidate：

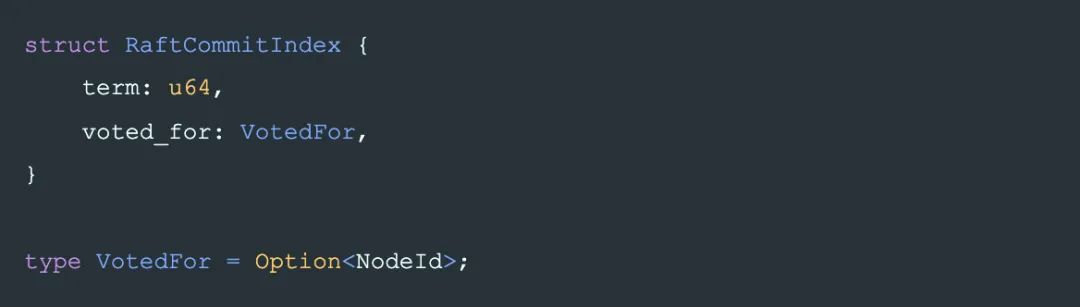
其中 VotedFor 的大小关系（即覆盖关系：大的可以覆盖小的）定义是：

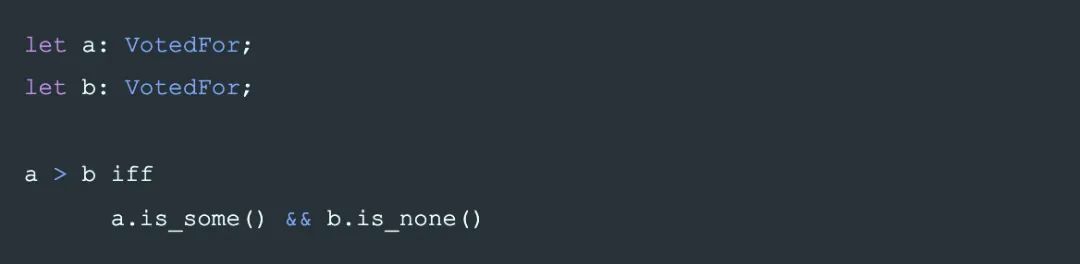
即，VotedFor 只能从 None 变化到 Some，不能修改。或者说，Some（A）和 Some（B）没有大小关系，这限制了 raft 选主时的成功几率.。导致了更多的选主失败冲突。

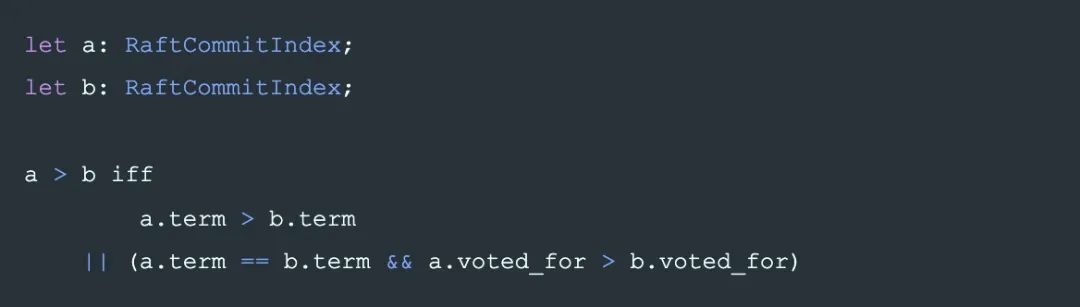
commit_index 在每条日志中的存储也做了简化，先看直接嵌入后的结构如下：

raft 中，因为 VotedFor 的特殊的偏序关系的设计，日志中 Term 相同则 voted_for 一定相同，所以最终日志里并不需要记录 voted_for，也能用来唯一标识日志，State，及用于比较 State 的大小。最终记录为：

这样的确让 raft 少记录一个字段, 但使得其含义变得更加隐晦，工程上也引入了一些问题, xp 并不欣赏这样的作法。

但不否认 raft 的设计在出现时是一个非常漂亮的抽象，主要在于它对 multi-paxos 没有明确定义的问题，即多条日志之间的关系到底应该是怎样的，给出了一个确定的答案。

概念对应关系:

abstract-Paxos	raft
writer at phase-1	Candidate
writer at phase-2	Leader
node	node
Writer.commit_index	(Term,VotedFor)
State.commit_index()	Term

成员变更方面，raft 的 joint 成员变更算法将条件限制为只允许 uniform 和 joint 交替的变更：c0 -> c0c1 -> c1 -> c1c2 -> c2 ....

不难看出，raft 的 单步变更算法也容易看出是本文的成员变更算法的一个特例。

Raft 的优化

abstract-paxos 通过推导的方式，得出的一致性算法可以说是最抽象最通用的。不像 raft 那样先给出设计再进行证明，现在从上向下看 raft 的设计，就很容易看出 raft 丢弃了哪些东西和给自己设置了哪些限制，也就是 raft 可能的优化的点：

一个 term 允许选出多个 leader：将 commit_index 改为字典序，允许一个 term 中先后选出多个 leader。

提前 commit：raft 中 commit 的标准是复制本 term 的一条日志到 quorum。这样在新 leader 刚刚选出后可能会延后 commit 的确认，如果有较多的较小 term 的日志需要复制的话。因此一个可以较快 commit 的做法是复制一段 State 时（raft 的 log），也带上 writer 的 commit_index 信息（即 raft leader 的 term）到每个 node，同时，对 State 的比较（即raft 的 log 的比较）改为比较【writer.commit_index, last_log_commit_index, log.len()】，在 raft 中，对应的是比较【leader_term, last_log_term, log.len()】。

成员变更允许更灵活的变化 ：例如 c0c1 -> c1c2.

其中 1,3 已经在 openraft 中实现（朋友说它是披着raft皮的paxos/:-)）。

Reference

Reference

可靠分布式系统-paxos的直观解释 : https://blog.openacid.com/algo/paxos/

abstract-paxos : https://github.com/openacid/abstract-paxos

(Not a) bug in Paxos : https://github.com/drmingdrmer/consensus-bugs#trap-the-bug-in-paxos-made-simple

leveldb : https://github.com/google/leveldb

openraft : https://github.com/datafuselabs/openraft

Two phase commit : https://en.wikipedia.org/wiki/Two-phase_commit_protocol

偏序关系 : https://zh.wikipedia.org/wiki/偏序关系

字典序 : https://zh.wikipedia.org/wiki/字典序

作者介绍：张炎泼（xp）Databend 分布式研发负责人
 

　　审核编辑：汤梓红